класи еквівалентності
Теорема. Нехай задано безліч A і U - відношення еквівалентності на A × A. Сукупність множин
Ua = b | (A, b) Про U>
утворює (після видалення співпадаючих) розбиття множини A.
Доведення. Доведемо перш за все, що якщо безлічі Ua і Ub перетинаються, то вони збігаються. Дійсно, якщо b Про Ua. то це означає, що (a, b) Про U. Але по транзитивності відносини з (a, b) Про U і (b, c) Про U слід (a, c) Про U. так що Ua ⊂ Ub.
В силу симетричності відносини ми маємо також a Про Ub. звідки Ub ⊂ Ua. і отже ці безлічі рівні.
Кожне таке підмножина, очевидно, непусто - воно визначається якимось входять в нього елементом. Кожен елемент безлічі (теж очевидно) належить одному з цих підмножин, тому ми отримали розбиття.
Підмножини, про які йде мова в теоремі, називаються класами еквівалентності. Скоро вони нам знадобляться.
Нехай задано відношення U. заданий на множині A. Часто потрібно транзитивно замкнути його: побудувати більше відношення TU. яке було б транзитивним і при цьому найменшим з усіх транзитивних відносин, що містять U.
TU: = U;
for i Про A do
for j Про A do
for k Про A do
if (j, i) Про TU ∧ (i, k) Про TU then
TU: = TU ∪
fi
od
od
od
Тут od - це закриває дужка для do. а fi - закриває дужка для if.
Алгоритм складається з початкового присвоювання і примітивного потрійного циклу по змінним i, j, k. в якому якщо в відношенні є пари (j, i) і (i, k). то в нього включається пара (j, k).
Хитрість полягає в тому, що алгоритм працює правильно, тільки якщо цикл по «проміжного індексу» i є зовнішнім. Ми повернемося до цього алгоритму пізніше. Буде доцільно розглянути відразу деякий його поліпшення.
Антисиметричною Транзитивне відношення U. заданий на множині A. визначає на цій множині частковий порядок. Завдяки йому, ми можемо порівнювати між собою елементи, але не всі елементи можна порівняти між собою.
При завданні часткового порядку, якщо пара елементів (a, b) належить U. то кажуть, що a передує b. Якщо жоден із цих двох елементів іншому не передує, але кажуть, що вони не порівнянні.
Умова антисиметричність тут необхідно для того, щоб виключити можливість еквівалентних елементів. Умова транзитивності потрібно для побудови ланцюжків.

Італійський економіст Вільфредо Парето (1848-1923) запропонував використовувати в таких завданнях конструкцію, яка в його честь називається кордоном Парето (Pareto frontier). Ми її зараз опишемо.
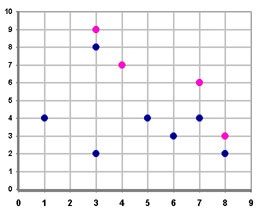
На малюнку безліч A складається з жирно намальованих точок на площині. Одна точка передує інший, якщо обидві її координати не менш відповідних координат інший, а хоча б одна з координат строго більше. В цьому випадку межа Парето складається з точок, пофарбованих у червоний колір.
Багатомісні відносини широко використовуються в одному з типів баз даних.
Інформація в реляційної базі даних зберігається таблицях. і кожна таблиця трактується як деякий багатомісне відношення. Наприклад, візьмемо фрагмент облікової картки студентської групи (такі використовуються в студотделе деканату)
Кожен рядок цієї таблиці (порядковий номер ми до рядку зараховувати не будемо) може розглядатися як набір з п'яти елементів: (ПІБ, №зач, Отм1, Отм2, Отм3). а значить, як елемент декартова твори п'яти множин SFIO × N × M1 × M2 × M3.
Таким чином, кожна така таблиця може розглядатися як п'ятимісне відношення.
У реляційних базах даних інформація задається сукупністю таких таблиць-відносин, і всі дії над інформацією і вимоги до неї описуються в термінах цих таблиць.