У практичній діяльності досить часто виникають ситуації, коли один потік платежів замінюється іншим потоком або одним платежем. При цьому дотримується незмінність фінансових відносин сторін до і після укладення контракту або, як кажуть, фінансова еквівалентність зобов'язань. Розрахунок платежів в цьому випадку базується на рівнянні еквівалентності.
Рівнянням еквівалентності є рівність сум замінних і замінюють платежів, приведених до одного моменту часу.
Принцип фінансової еквівалентності зобов'язань дозволяє, зокрема, порівнювати два окремих платежу, що виплачуються в різні моменти часу. При цьому використовуються прості відсотки, якщо терміни платежів менше року, і складні відсотки - якщо терміни більше року.
Нехай є два платежу і з термінами відповідно і. При оцінці цих платежів порівнюються їх сучасні вартості, і той платіж вважається великим, у якого більше його сучасна вартість. Іноді виникає необхідність у визначенні критичної ставки. при якій два розглянутих платежу виявляються рівними. Розглянемо два варіанти.
1. Для простих відсотків критична ставка знаходиться з рівняння еквівалентності, одержуваного шляхом прирівнювання сучасних вартостей першого і другого платежів
Вирішуючи це рівняння відносно. знайдемо
Приклад 3.15. Перший платіж, що дорівнює 900 руб. повинен бути виплачений через 30 днів, а другий, що дорівнює 920 руб. виплачується через 270 днів. Порівняти ці платежі при простій процентній ставці 15% річних і при базі К = 360.
Рішення. Сучасна вартість першого платежу
Сучасна вартість другого платежу
При заданій ставці перший платіж перевищує другий.
Приклад 3.16. Перший платіж, що дорівнює 900 руб. повинен бути виплачений через 30 днів, а другий, що дорівнює 920 руб. виплачується через 270 днів. Визначити критичну ставку при базі К = 360.
Рішення. Критична ставка, при якій платежі еквівалентні, визначається за формулою
2. Для складних відсотків рівняння еквівалентності має вигляд
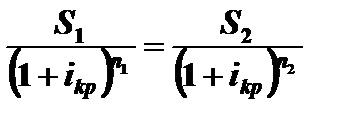
Вирішуючи це рівняння відносно. знайдемо
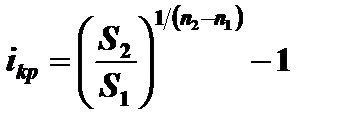
Приклад 3.17. Перший платіж, що дорівнює 9 тис. Руб. повинен бути виплачений через 2 роки, а другий, що дорівнює 12 тис. руб. виплачується через 5 років. Порівняти ці платежі при складній процентній ставці 15% річних.
Рішення. Сучасна вартість першого платежу
Сучасна вартість другого платежу
При заданій ставці перший платіж перевищує другий.
Приклад 3.18. Перший платіж, що дорівнює 9 тис. Руб. повинен бути виплачений через 2 роки, а другий, що дорівнює 12 тис. руб. виплачується через 5 років. Визначити критичну ставку.
Рішення. Критична ставка, при якій платежі еквівалентні, визначається за формулою
Об'єднання потоку платежів в один називається також консолідацією платежів. При цьому визначають або суму консолідованого платежу при відомому терміні, або термін при відомій сумі. Розглянемо спочатку завдання визначення суми консолідованого платежу при відомому терміні. Це завдання може бути сформульована таким чином: нехай платежі з номерами 1, 2. m і з термінами, прономерованнимі відповідно, замінюються одним в сумі з відомим терміном. Визначити. У загальному випадку термін може лежати між першою і останньою виплатами замінних платежів. Схема виплат може бути представлена так, як показано на рис. 3.7.
Тут всім платежам до моменту n0 присвоєно номер t івсего таких платежів Т, а платежах після моменту n0 присвоєно номер k івсего таких платежів K .Загальна кількість замінних платежів m = T + K. Сума консолідованого платежу при нарахуванні простих відсотків визначається за формулою
В першу суму входять всі нарощені платежі з термінами менше терміну консолідованого платежу, а в другу суму входять всі дисконтовані платежі з термінами більше терміну консолідованого платежу. Якщо термін консолідованого платежу настане пізніше останнього терміну замінних платежів, то ця формула набуває вигляду
Приклад 3.19. Три платежу 5 тис. Руб. з терміном 130 днів, 3 тис. руб. з терміном 165 днів і 8 тис. руб. з терміном 320 днів замінюються одним з терміном 250 днів. Сторони домовилися про використання простої процентної ставки 20% річних. Визначити суму консолідованого платежу при базі К = 365.
Рішення. Схема виплат представлена на рис. 3.8.
0 130 165 250 320 n. днів
При визначенні суми консолідованого платежу використовується рис. 3.8.
Сума консолідованого платежу при нарахуванні складних відсотків визначається за формулою
Якщо термін консолідованого платежу настане пізніше останнього терміну замінних платежів, то ця формула набуває вигляду
Приклад 3.20. Три платежу 5 тис. Руб. з терміном 2 роки, 4 тис. руб. з терміном 4 роки і 6 тис. руб. з терміном 5 років замінюються одним з терміном 3 роки. Сторони домовилися про використання складної процентної ставки 25% річних. Визначити суму консолідованого платежу.
Рішення. Схема виплат представлена на рис. 3.9.
При визначенні суми консолідованого платежу використовується рис. 3.9.
0 2 3 4 5 n. років
При визначенні терміну консолідованого платежу рівняння еквівалентності представляють як рівність сучасних вартостей замінних і консолідованого платежів. У цьому випадку схема виплат може бути представлена так, як показано на рис. 3.10.
Відповідно до позначеннями рис. 3.10 рівняння еквівалентності для простих відсотків має вигляд
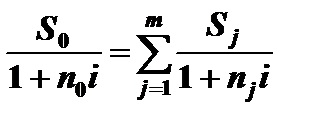
Суму в правій частині цього рівняння позначимо літерою U, тобто
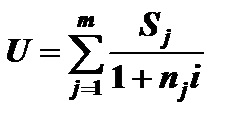
Тоді рішення рівняння еквівалентності щодо має вигляд
Приклад 3.21. Три платежу 8 тис. Руб. з терміном 130 днів, 10 тис. руб. з терміном 160 днів і 4 тис. руб. з терміном 200 днів замінюються одним в розмірі 21 тис. руб. Сторони домовилися про використання простої процентної ставки 20% річних. Визначити термін консолідованого платежу при базі К = 365.
Рішення. Схема виплат представлена на рис. 3.11.
21000 8000 10000 4000 S. руб.
При визначенні сучасної вартості замінних платежів використовується рис. 3.11.
Термін консолідованого платежу знаходиться за формулою
Визначимо термін в днях за формулою
Відповідно до позначеннями рис. 3.11 рівняння еквівалентності для складних відсотків має вигляд
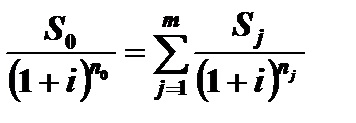
Суму в правій частині цього рівняння позначимо літерою U, тобто
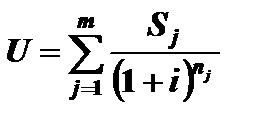
Тоді рівняння еквівалентності можна записати у вигляді
Прологаріфміровав ліву і праву частини цього рівняння, знайдемо
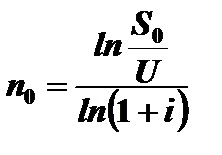
Приклад 3.22. Три платежу 2 тис. Руб. з терміном 2 роки, 4 тис. руб. з терміном 3 роки і 3 тис. руб. з терміном 4 роки замінюються одним в розмірі 8 тис. руб. Сторони домовилися про використання складної процентної ставки 18% річних. Визначити термін консолідованого платежу.
Рішення. Схема виплат представлена на рис. 3.12.
При визначенні сучасної вартості замінних платежів використовується рис. 3.12.
Термін консолідованого платежу знаходиться за формулою
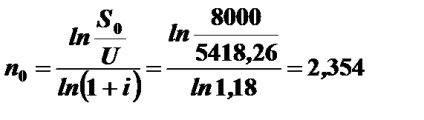
1. Які потоки платежів називаються регулярними?
2.Дати визначення нарощеної суми і сучасної вартості потоку платежів.
3. Які ренти називаються постійними?
4.Дать визначення річної ренти, ренти з нарахуванням відсотків за номінальною відсоткової ставки, р - термінової ренти, безперервної ренти.
5. Як змінюються нарощена сума і сучасна вартість ренти пренумерандо в порівнянні з рентою постнумерандо?
6.Напісать формулу для сучасної вартості вічної ренти.
7.Опісать метод розрахунку величини річної виплати ренти.
8. Описати метод розрахунку терміну ренти.
9.Опісать метод розрахунку процентної ставки ренти.
10.Що таке фінансова еквівалентність зобов'язань?
11.Дать визначення рівняння еквівалентності.
12.Опісать принцип розрахунку суми консолідованого платежу при використанні простої і складної процентних ставок.
13.Опісать принцип розрахунку терміну виплати консолідованого платежу.