У практиці нерідко виникають випадки, коли необхідно замінити одне зобов'язання іншим, наприклад з більш віддаленим терміном платежу, достроково погасити заборгованість, об'єднати кілька платежів в один (консолідувати платежі) і т.п. У таких ситуаціях неминуче виникає питання про принцип, на якому має базуватися зміна контракту. Таким загальноприйнятим принципом є фінансова еквівалентність зобов'язань, яка передбачає незмінність фінансових відносин сторін до і після зміни контракту.
Еквівалентними вважаються такі платежі, які, будучи "наведені" до одного моменту часу (focal date), виявляються рівними. Приведення здійснюється шляхом дисконтування до більш ранньої дати або, навпаки, нарощення суми платежу (якщо ця дата відноситься до майбутнього). Якщо при зміні умов принцип фінансової еквівалентності не дотримується, то одна з сторін-учасниць терпить збитки, розмір якого можна заздалегідь визначити. По суті, принцип еквівалентності випливає з формул нарощення і дисконтування, що зв'язують величини Р і S. Сума Р еквівалентна S при прийнятій відсотковій ставці і метод її нарахування. Дві суми грошей S1 і S2, що виплачуються в різні моменти часу, вважаються еквівалентними, якщо їх сучасні (або нарощені) величини, розраховані за однією і тією ж процентною ставкою і на один момент часу, однакові. Заміна S1 на S2 в цих умовах формально не змінює відносини сторін.
Приклад 3.1. Є два зобов'язання. Умови першого: виплатити 400 тис. Руб. через чотири місяці; умови другого: виплатити 450 тис. руб. через вісім місяців. Чи можна вважати їх рівноцінними? Так як платежі короткострокові, то при дисконтуванні на початок терміну застосуємо просту ставку, рівну, припустимо, 20%, і отримаємо:
= 375,00; = 397,06 тис. Руб.
Як бачимо, порівнювані зобов'язання не є еквівалентними при заданій ставці і в силу цього не можуть адекватно заміняти один одного.
Порівняння платежів передбачає використання певної відсоткової ставки, і, отже, результат залежить від вибору її величини. Однак, що практично дуже важливо, така залежність не настільки жорстка, як це може здатися на перший погляд. Припустимо, що порівнюються два платежу S1 і S2 з термінами п1 і n2. вимірюваними від одного моменту часу, причому S1 З ростом i величина Р зменшується, причому при i = i0 спостерігається рівність Р1 = Р2. Для будь-якої ставки i 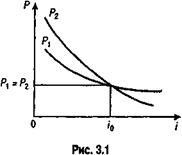
З формули (3.1) випливає, що чим більше розходження в термінах, тим більше величина i0 при всіх інших рівних умовах. Зростання відносини S1 / S2 надає протилежний вплив.
Приклад 3.2. Для даних прикладу 3.1 отримаємо:
Таким чином, співвідношення Р2> Р1 справедливо для будь-якого рівня процентної ставки, яка менше 42,8%.
Якщо дисконтування проводиться за складною ставкою, то критичну ставку знайдемо з рівності
Графічна ілюстрація залежності Р від i наведена на рис. 3.1.
Приклад 3.3. Порівнюються два платежу: 2 млн. Руб. з виплатою через два роки і 3 млн. руб. з виплатою через чотири роки. Відповідно до формули (3.2) критичний рівень складної процентної ставки дорівнює:
i0 = - 1 = 0,2247, або 22,47%.
При будь-ставкою, яка менше критичної, сучасна вартість першого варіанту більше другого.