Прямі та площини загального положення не паралельні і не перпендикулярні до жодної з площин проекцій. І відрізняються тим, що при проектуванні їх метричні характеристики (відстані, кути і площі) піддаються перекручуванню (Рис.16). На наведеному прикладі жодна з проекцій відрізка не дорівнює довжині самого відрізка, спотворені і кути нахилу відрізка до площин і. І, нарешті, площа жодної проекції трикутника не дорівнює площі самого трикутника. Примітка: кути нахилу прямої до площин проекцій, як правило, мають особливі позначення (кут - до площини, - до і - до). Основи Web технологій - курс лекцій Введення в web-дизайн Графіка в web-дизайні Корисні прийоми
Геометричні фігури - приватного положення паралельні або перпендикулярні до однієї з площин проекцій. У першому випадку це прямі і площини рівня, у другому - прямі і площини проектують.
Прямі рівня: горизонталь (), фронталь () і профільна пряма (). За їх назвою стає зрозуміло, щодо якій площині проекцій кожна з них паралельна. Cтадіі розробки конструкторської документації Залежно від стадій pазpаботки, встановлюваних ГОСТ 2.103 - 68, констpуктоpскіе документи подpазделяются на ПPОЕКТHИЕ і робоча.
Площині рівня: горизо-нтальная, фронтальна і профільна.
Креслення прямих і площин рівня відрізняються перш за все тим, що метричні характеристика цих фігур проектуються без спотворення. Прикладом може служити Рис.17.
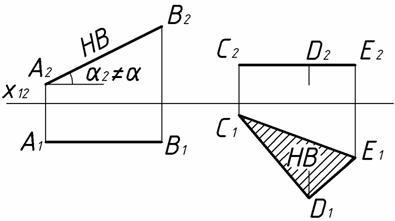
Фронталь. На фронтальній проекції фронталі відображаються натуральна величина відрізка () і натуральна величина його нахилу відрізка до горизонтальної площини проекцій. При цьому горизонтальна проекція відрізка, природно, паралельна осі. Для розмірів, відмінних від лінійних, застосовують умовні знаки: Ø - означає діаметр, R - радіус, # 8298; - квадрат, - ухил, - конусність, ° - градус
Тут же трикутник - в горизонтальній площині. Горизонтальна проекція трикутника відображає натуральну величину його площі. Що стосується фронтальної проекції трикутника, то вона вироджується в пряму лінію, паралельну осі.
Особливість вироджених проекції будь-якої геометричної фігури полягає в тому, що вона володіє збірним властивістю. Це означає, що будь-яка точка фігури отримує своє відображення на цій проекції.