Властивості основного завдання лінійного програмування пов'язані з властивостями опуклих множин.
Безліч точок називається опуклим, якщо воно разом з будь-якими двома точками містить і їх довільну опуклу комбінацію.
Геометричний сенс цього визначення полягає в тому, що безлічі разом з його довільними точками повністю належить і прямолінійний відрізок, їх з'єднує. Прикладами опуклих множин є прямолінійний відрізок, напівплощина, коло, куля, куб, полупространство і ін.
Кутовими точками опуклого безлічі називаються точки, які не є опуклою комбінацією двох довільних точок безлічі. Наприклад, кутовими точками трикутника є його вершини, кола - точки окружності, які його обмежують.
Безліч планів основного завдання лінійного програмування є опуклим (якщо воно не порожньо). Непорожнє безліч планів називається многогранником рішень, а всяка кутова точка багатогранника рішень - вершиною.
Якщо основне завдання лінійного програмування має оптимальний план, то цільова функція задачі приймає максимальне значення в одній з вершин багатогранника рішень. Якщо максимальне значення досягається більш ніж в одній вершині, то цільова функція приймає його у всякій точці, що є опуклою лінійною комбінацією цих вершин.
Непорожнє безліч планів основного завдання лінійного програмування утворює опуклий багатогранник, кожна вершина якого визначає опорний план. Для одного з опорних планів (тобто в одній з вершин багатогранника рішень) значення цільової функції є максимальним (за умови, що функція обмежена зверху на безлічі планів).
Вершину багатогранника рішень, в якій цільова функція приймає максимальне значення, можна знайти досить просто, якщо завдання в стандартній формі містить не більше двох змінних:
Перетин півплощини, яке визначається системою лінійних нерівностей, називається областю рішень (ОР) системи, а якщо вона задовольняє умовам позитивності. то називається областю допустимих рішень (ОДР).
Якщо система нерівностей сумісна, то областю допустимих рішень задачі є опукле безліч, яке називається багатокутником рішень. Сторони цього багатокутника лежать на прямих, рівняння яких виходять з вихідної
системи обмежень заміною знаків нерівностей на знаки точних рівностей.
Рішення задачі лінійного програмування геометричним методом включає наступні етапи.
1. На площині будують прямі, рівняння яких виходять в результаті заміни в обмеженнях знаків нерівностей на знаки точних рівностей.
2. Знаходять півплощини, що визначаються кожним з обмежень задачі.
3. Будують багатокутник рішень.
4. Будують вектор, який вказує напрям зростання цільової функції.
5. Будують початкову пряму цільової функції і потім пересувають її паралельно самій собі в напрямку вектора до крайньої кутовий точки багатокутника рішень. В результаті знаходять точку, в якій цільова функція приймає максимальне значення, або безліч точок з однаковим максимальним значенням цільової функції альтернативний оптимум, якщо початкова пряма зливається з однією з сторін багатокутника рішень, або встановлюють необмеженість зверху функції на безлічі планів.
6. Визначають координати точки максимуму функції і обчислюють значення цільової функції в цій точці. Мінімальне значення лінійної функції мети знаходиться шляхом пересування початковій прямій в напрямку, протилежному вектору.
Приклад 1. Знайдіть максимум і мінімум лінійної функції
Рішення. Побудуємо на площині багатокутник рішень (рис. 1). Для цього в нерівностях системи обмежень і умов невід'ємності змінних знаки нерівностей замінимо на знаки точних рівностей.
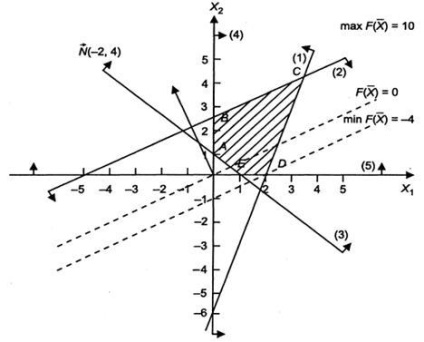
Малюнок 1. Побудова багатокутника рішень
Побудувавши прямі системи, знайдемо відповідні напівплощини і їх перетину.
Багатокутником рішень завдання є п'ятикутник ABCDE, координати точок якого задовольняють умові незаперечності змінних і нерівностей системи обмежень задачі.
Для знаходження точок екстремуму побудуємо початкову пряму і вектор (-2, 4). Пересуваючи пряму в напрямку вектора, знайдемо точку С, в якій початкова пряма приймає положення опорної прямої. Отже, в точці С цільова функція має максимальне значення. Так як точка С отримана в результаті перетину прямих 1
і 2 з системи, то її координати задовольняють рівнянням цих прямих:
Вирішивши систему рівнянь, отримаємо: = 3,4; = 4,2; звідки знайдемо максимальне значення цільової функції = (- 2) * 3,4 + 4 * 4,2 = 10.
За умовою завдання початкова пряма паралельна прямій (2), так як коефіцієнти при змінних. пропорційні: (-2) / (- 1) = 4/2 = 2. Отже, початкова пряма займе положення опорної прямої в точках В, С і в будь-якій точці відрізка ВС, в яких приймає одне і те ж максимальне значення. Для визначення координат точки В вирішимо систему двох лінійних рівнянь:
Максимальне значення цільової функції в точці В дорівнює:
Запишемо безліч оптимальних рішень як лінійну опуклу комбінацію кутів точок відрізка ВС: де.
Підставивши координати кутових точок, отримаємо:
Підставляючи будь-які значення а від 0 до 1, отримаємо координати безлічі точок відрізка ВС, в кожній з яких цільова функція приймає максимальне значення, рівне 10.
Для знаходження мінімального значення цільової функції завдання переміщаємо початкову пряму в напрямку, протилежному вектору. Початкова пряма займе положення опорної прямої в вершині D, де = 2, = 0, а мінімальне значення цільової функції дорівнює: = (- 2) * 2 + 4 * 0 = -4.
Приклад 2. Геометричний метод рішення задачі лінійного програмування розглянемо на прикладі поставленого завдання і побудованої моделі комерційної діяльності підприємства, представленої в п. 2.2.1. Так як модель має тільки дві змінні,
то це завдання можна вирішити геометричним методом.
Побудуємо на площині (рис. 1) багатокутник допустимих рішень задачі. Для цього в нерівностях системи обмежень знаки нерівностей замінимо на знаки точних рівностей:
Побудувавши отримані обмежують прямі, знайдемо відповідні напівплощини припустимих значень змінних, а потім їх перетин (рис. 1).
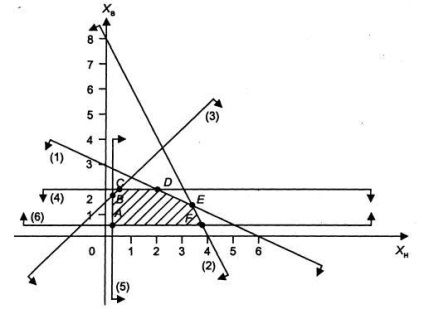
Рис.1 Побудова області допустимих рішень
Напрямок стрілок від кожної граничній прямій визначається шляхом безпосередньої підстановки в нерівність координат довільно взятої точки, наприклад (0; 0), і при задоволенні даного нерівності направляємо стрілки в бік контрольної точки, в іншому випадку - навпаки.
Отримана область рішень є багатокутник ABCDEF.
Кутові точки багатокутника рішень мають наступні координати:
А (0,25; 0,5), В (0,25; 1,75), С (0,5; 2), D (2; 2), Е (3; 1), F (3,75 ; 0,5).
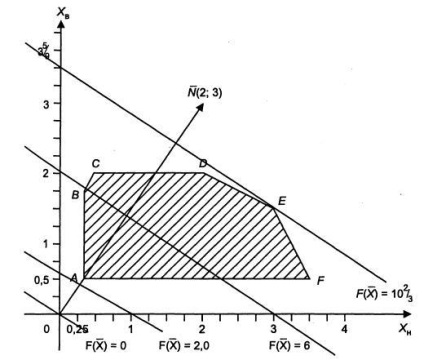
Для знаходження мінімуму і максимуму цільової функції будуємо початкову пряму і вектор-градієнт (2; 3) (рис. 2). Координатами вектора є коефіцієнти лінійної цільової функції при змінних і. Для побудови графіка цільової функції задаємо довільне значення .Якщо = О, то пряма проходить через початок координат. Для її побудови, вважаючи = 1, отримаємо = -2 / 3, а при = 1, отримаємо = -3 / 2 (рис. 2). Вважаючи = 6, таким же чином побудуємо лінію цільової функції.
Потім для = 0,25 і = 0,5 визначаємо мінімальне значення = 2. Таким чином, побудуємо на графіку ряд паралельних прямих (рис. 2), де вектор-градієнт (2; 3) показує напрямок росту цільової функції.
Максимальне значення буде в точці Е. Оскільки точка Е отримана в результаті перетину прямих (1) і (2), то для определеніяее координат вирішимо систему рівнянь:
Максимальне значення цільової функції
Цільова функція перетинає вісь у точці =. а вісь в точці =.