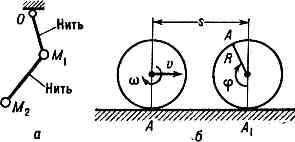
механічні. системи, в яких брало все зв'язку (див. ЗВ'ЯЗКУ МЕХАНІЧНІ) явл. геометричними (голономних), т. е. налагающими обмеження тільки на положення (або на переміщення за час руху) точок і тіл системи, але не на величини їх швидкостей. Напр. подвійний маятник (рис. а) явл. Г. с .; в ньому зв'язку (нитки) накладають обмеження лише на положення або переміщення вантажів М1 і М2, але не на їх швидкості, к-які при русі можуть мати будь-які значення. Зв'язок, що накладає обмеження на швидкості точок і тіл системи, т. Е. Що встановлює між цими швидкостями потужність. співвідношення, наз. кинематической. Однак якщо ці співвідношення можна звести до геометричних, т. Е. До співвідношень між переміщеннями (або координатами) точок і тіл системи, то такий зв'язок також явл. голономних. Напр. при коченні без ковзання колеса радіуса R за прямолінійним рельсу (рис. б) швидкість v центру колеса і кут. швидкість w колеса пов'язані співвідношенням v = Rw, але його можна звести до геом. співвідношенню s = Rj між переміщенням s = AA1 центру і кутом повороту j колеса. Отже, це Г. с.
Кінематіч. зв'язку, що не зводяться до геометричних, наз. неголономними, а механічні. системи з такими зв'язками - неголономними системами. Поділ механічні. систем на голономні і неголономні дуже істотно, т. к. ряд ур-ний, що дозволяють порівняно просто вирішувати завдання механіки (див. Лагранжа Рівняння механіки), застосовується лише до Г. с.
Дивитися що таке "голономних СИСТЕМИ" в інших словниках:
Голономні системи - механічні системи, в яких всі зв'язки (див. Зв'язки механічні) є геометричними (голономних), тобто налагающими обмеження тільки на положення (або переміщення за час руху) точок і тіл системи, але не на величини їх ... ... Велика радянська енциклопедія
Неголономні системи - механічні системи, на які, крім геометричних, накладаються ще кінематичні зв'язку, що не зводяться до геометричних і звані неголономними (див. Голономні системи). Прикладом Н. с. є куля, що котиться без проковзування по ... Велика радянська енциклопедія
Неголономними СИСТЕМИ - механічні. системи, на до риє, крім геометричних, накладаються ще кінематіч. зв'язку, що не зводяться до геометричних і зв. неголономними (див. голономних СИСТЕМИ). Приклад Н. с. куля, що котиться без проковзування по шорсткою площині. При цьому ... ... Фізична енциклопедія
ЗВ'ЯЗКУ МЕХАНІЧНІ - обмеження, що накладаються на положення або руху механічні. системи. Зазвичай С. м. Здійснюються за допомогою к. Н. тел. Приклади таких С. м. Поверхню, по до рій ковзає або котиться тіло; нитка, на до рій підвішений вантаж; шарніри, що з'єднують ланки ... ... Фізична енциклопедія
Лагранжа рівняння - 1) в гідромеханіці рівняння руху жид кой середовища, записані в змінних Лагранжа, якими є координати частинок середовища. З Л. у. визначається закон руху частинок середовища у вигляді залежностей координат від часу, а по ним ... ... Велика радянська енциклопедія
Зв'язки механічні - обмеження, що накладаються на положення або рух механічної системи. Зазвичай С. м. Здійснюються за допомогою яких нибудь тел. Приклади таких С. м. Поверхню, по якій ковзає або котиться тіло; нитка, на якій підвішений вантаж; ... ... Велика радянська енциклопедія
Ступенів свободи число - в механіці, число незалежних між собою можливих переміщень (Див. Можливі переміщення) механічної системи. С. с. ч. залежить від числа матеріальних частинок, що утворюють систему, і числа і характеру накладених на систему зв'язків ... ... Велика радянська енциклопедія
Пуанкаре Рівняння - загальні рівняння механіки голономних систем, представимо за допомогою недо рій групи Лі нескінченно малих перетворень. Нехай х i, i = 1. п, змінні, що визначають положення голономних механічні. системи, обмеженої ідеальними зв'язками, ... ... Математична енциклопедія
Голономний зв'язок - голономний зв'язок механічний зв'язок, що накладає обмеження лише на положення (або переміщення) точок і тіл системи. Математично виражається у вигляді рівності [1]: де qj узагальнені координати, що описують механічну систему, i = 1 ... k ... Вікіпедія