Експериментальні дані можуть виражатися у вигляді таблиць, графіків, а також за допомогою математичних рівнянь.
Табличний спосіб запису експериментальних даних є найбільш простим і широко поширеним, повністю відтворює отримані результати. Однак табличний спосіб менш наочний в порівнянні з графічним.
Графічний метод дозволяє наочно оцінити зміни змінних величин, встановити характер цієї зміни, а також за допомогою цього методу можна без особливих обчислень знайти проміжні значення змінних величин.
Крім цього, графічні методи обробки експериментальних даних допомагають вивести емпіричну формулу в тих випадках, коли досліджувані процеси не підкоряються вже відомим теоретичним законам. Тоді за експериментальними даними встановлюється вид формули і постійні коефіцієнти.
Табличний спосіб запису. У дослідженнях за технологією бетону часто доводиться визначати залежність між окремими змінними величинами. При наявності можливості вільно задаватися чисельними значеннями незалежних змінних все досліди повинні розбиватися на ряд серій з таким розрахунком, щоб в кожній серії одна з незалежних змінних залишалася постійною величиною. Наприклад, необхідно знайти залежність між трьома змінними, з яких -іскомая, В / Ц - зміна змінних в наступних межах:
Для рівномірного розподілу значень змінних і В / Ц можна записати: для 5 значень, а для В / Ц - 7 значень.
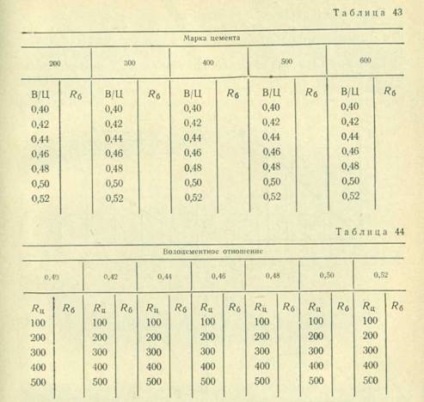
Форма запису по змінній # ц матиме вигляд, наведений в табл. 43.
Форма запису по переміщеної В / Ц матиме вигляд, наведений в табл. 44.
Таким чином отримали п'ять серій дослідів, кожна при своїй постійному значенні змінної, і сім дослідів в кожній серії. При наявності таблиці можна на одному графіку побудувати криві залежності невідомої величини від змінної В / Ц при приватних значеннях змінної. При наявності таблиці легко побудувати графік залежності невідомої від змінної при приватних значеннях змінної В / Ц. При наявності таких графіків легше підшукати і вивести залежність між трьома змінними.
Вибір масштабу шкали при побудові графіків. При побудові графічної залежності змінних величин користуються рівномірними і нерівномірними шкалами. Рівномірною шкалою при зображенні функції в прямокутних координатах називають таку, на якій відстані між двома поділами, відповідними зміни змінної на одну і ту ж величину, рівні.
Якщо відстані між двома поділами, відповідними зміни змінної на одну і ту ж величину, не рівні, таку шкалу називають нерівномірною (логарифмічною квадратичної шкалою і т. Д.).
Масштаби по осях координат для рівномірних шкал зазвичай приймають рівними. Однак в деяких випадках при значній різниці в межах зміни змінних величин не вдається застосувати рівні масштаби, тоді на осях координат застосовують різні масштаби шкал, але обов'язково з таким розрахунком, щоб побудовані на цьому графіку криві були наочними і сам графік вийшов би найбільш компактним.
Застосування різних масштабів шкал не позначається на точності відліків, якщо на графіку виходить пряма лінія, так як зі зміною масштабів зміниться лише тільки її нахил (рис. № 198).
Якщо ж на графіку виходить крива лінія, то в цьому випадку при застосуванні різних масштабів крива буде спотворюватися, що може привести до зниження точності відліків і ввести в оману дослідника при складанні висновків. Якщо на графіку залежності двох змінних величин виходить крива лінія, слід користуватися на обох осях шкалами з рівними масштабами.
Побудова логарифмічної шкали грунтується на властивості логарифмів, що полягає в тому, - що якщо будь-яке число збільшити у 10, 100 і т. Д. Раз, то отриманий логарифм нового числа, зберігаючи свою мантиссу, збільшить тільки характеристику цього числа відповідно на 1, 2, 3 і т. д. так, якщо 6 = 0,78, а 60 = 1,78, то для отримання відрізка, що відповідає 1д60, т. е. 1,78, потрібно на осі відкласти відрізок, рівний 0,78, так як довжина шкали для значень х від 1 до 10 приймається рівною одиниці (lg 10 = 1).
Для побудови логарифмічною шкали беруть дві паралельні прямі і на одній з них (верхній) будують рівномірну шкалу від 0 до 1. Потім визначають значення логарифмів цілих чисел від 1 до 10, відзначають на верхній шкалі точки, що відповідають значенням gx і переносять їх на нижню пряму , записуючи кожної перенесеної точці відповідне значення х (рис. № 199). Логарифмічна шкала на осях координат дозволяє випрямити одержувані криві залежності досліджуваних величин і спрощує побудову деяких рівнянь.
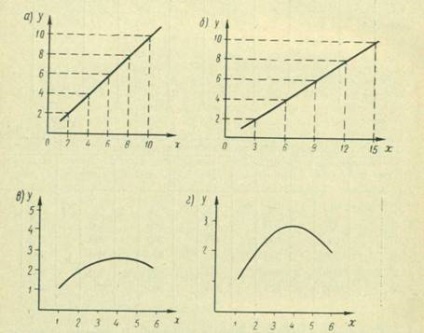
рис. № 198. Побудова графіка залежності в прямокутних координатах:
А - з рівними масштабами шкал для прямої; б -з різними масштабами шкал для прямої; в - з рівними масштабами шкал для кривої; г - з різними масштабами шкал для кривої
рис. № 199. Побудова логарифмічної шкали функції довжиною в два модуля