Розглянемо Нелін ?? ейную систему, схема якої представлена на ріс.12.2, а. Система складається з лин ?? єйної частини з передавальної функцією Wл (s) і Нелін ?? ейного ланки НЛ з конкретно заданої характеристикою. Ланка з коефіцієнтом - 1 показує, що зворотний зв'язок в системі негативна. Вважаємо, що в системі існують автоколивання, амплітуду і частоту яких ми хочемо знайти. В даному режимі вхідна величина Х Нелін ?? ейного ланки і вихідна Y є періодичними функціями часу.
Метод гармонійної лин ?? еарізаціі заснований на nредnоложеніі, що коливання на вході Нелін ?? ейного ланки є сінусоідальни.мі, т. е. що
гдеА- амплітуда і - частота цих автоколивань. а - можлива в загальному випадку постійна складова, коли автоколивання несиметричні.
Насправді автоколебания в Нелін ?? ейних системах нд ?? егда несинусоїдальний внаслідок спотворення їх форми нелі-нійним ланкою. З цієї причини вказане вихідне припущення озна-чає, що метод гармонійної лин ?? еарізаціі є принципово наближеним і область його застосування обмежена випадками, коли автоколивання на вході нелі-лінійного ланки досить близькі до синусоїдальним. Для того щоб це мало місце, лин ?? ейная частина системи повинна не пропускної-скать вищих гармонік автоколебаний, т. Е. Бути фільтром нижніх частот. Останнє ілюструється рис. 12.2, б. У разі якщо, наприклад, частота автоколивань дорівнює, то лин ?? ейная частина з показаної на рис. 12.2, б АЧХ буде грати роль фільтра нижніх частот для цих коливань, так як вже друга гармоніка, частота якої дорівнює 2, практично не пройде на вхід Нелін ?? ейного ланки. Отже, в даному випадку метод гармонійної лин ?? еарізаціі застосуємо.
У разі якщо частота автоколивань дорівнює, лин ?? ейная частина буде вільно пропускати другу, третю і інші гармоніки автоколивань. У цьому випадку не можна стверджувати, що коливання на вході Нелін ?? ейного ланки будуть досить близькі до синусоїдальним, ᴛ.ᴇ. необхідна для застосування методу гармонійної лин ?? еарізаціі передумова не виконується.
Для того щоб встановити, чи є лин ?? ейная частина си-стеми фільтром нижніх частот і тим самим визначити застосуй-ність методу гармонійної лин ?? еарізаціі, вкрай важливо знати частоту автоколивань. При цьому її можна дізнатися тільки в резуль-таті використання цього методу. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, пpімeнімocть методу гармонійної лuнеарuзацuu прuходuтся визначати вже в кінці uсследованuя в порядку перевірки.
Зауважимо при цьому, що якщо в результаті цієї перевірки гіпо-теза про те, що лин ?? ейная частина системи грає роль фільтра ниж-них частот, не підтверджується, це не означає ще невірності отриманих результатів, хоча, зрозуміло, ставить їх під сом -нен і вимагає додаткової перевірки будь-яким іншим способом.
Отже, припустивши, що лин ?? ейная частина системи є фільтр нижніх частот, вважаємо, що автоколивання на вході Нелін ?? ейного ланки синусоїдальна, тобто мають вигляд (12.1). Коливання на виході цієї ланки будуть при цьому вже несинусоїдальними внаслідок їх спотворення Нелін ?? ейностью. Як приклад на рис. 12.3 побудована крива на виході Нелін ?? ейного ланки для определ ?? енной амплітуди вхідного чисто синусоїдального сигналу за влучним висловом ланки, наведеної там же.
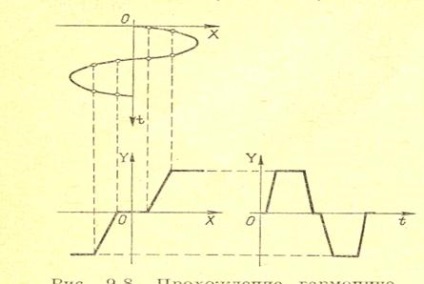
Рис.12.3. Проходження гармонійного коливання через Нелін ?? ейное ланка.
При цьому, оскільки ми вважаємо, що лин ?? ейная частина системи пропускає лише основну гармоніку автоколебаний, має сенс цікавитися тільки цієї гармонікою на виході Нелін ?? ейного ланки. З цієї причини розкладемо вихідні коливання в ряд Фур'є і відкинемо вищі гармоніки. В результаті отримаємо:
Перепишемо вираз (12.2) в більш зручному для подальшого використання вигляді, підставивши в нього виходять з (12.1) такі вирази для і:
Підставивши ці вирази в (12.2), будемо мати:
Тут введені позначення:
Диференціальне рівняння (12.5) справедливо для синусоїдального вхідного сигналу (12.1) і визначає вихідний сигнал Нелін ?? ейного ланки без урахування вищих гармонік.
Коефіцієнти відповідно до виразами (12.3) для коефіцієнтів Фур'є є функціями постійної складової, амплітуди А і частоти автоколивань на вході Нелін ?? ейного ланки. При фіксованих А. і рівняння (12.5) є лин ?? ейним. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, в разі якщо відкинути вищі гармоніки, то для фіксованого гармонійного сигналу вихідне Нелін ?? ейное ланка повинна бути замінено еквівалентним лин ?? ейним, описуваних рівнянням (12.5). Ця заміна і прийнято називати гармонійної лин ?? еарізаціей.
На рис. 12.4 умовно зображена схема цієї ланки, що складається з двох паралельних ланок.
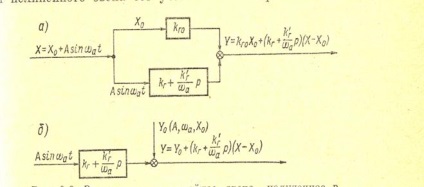
Мал. 12.4. Еквівалентну лин ?? ейное ланка, отримане в результаті гармонійної лин ?? еарізаціі.
Одна ланка () пропускає постійну складову, а інше - тільки синусоидальную складову автоколебаний.
Коефіцієнти називаються коефіцієнтами гармонійної лин ?? еарізаціі або гармонійними коефіцієнтами передачі. - коефіцієнт передачі постійної складової, а - два коефіцієнти передачі синусоїдальної складової автоколебаний. Ці коефіцієнти визначаються Нелін ?? ейностью і значеннями і за формулами (12.3). Існують определ ?? енние за цими формулами готові виро-вання для для ряду типових Нелін ?? ейних ланок. Для цих і взагалі вс ?? ех безінерційних Нелін ?? ейних ланок вели-чини не залежить від і є функціями тільки амплітуди А і.
Постійна складова на виході Нелін ?? ейного ланки (див. Рівняння 12.2, 12.4) з'являється по одній з двох причин: якщо до системи докладено зовнішнє постійний вплив, що створює (див. Рівняння 12.1), або якщо характеристика Нелін ?? ейного ланки несиметрична щодо початку коорди-нат, внаслідок чого відбувається явище випрямлення вхідного синусоїдального сигналу.
При гармонійної лин ?? еарізаціі Нелін ?? ейних ланок з такими характеристиками можна висловлювати через за допомогою коеф-фициента гармонійної лин ?? еарізаціі, т. е. у вигляді
так як тут і при. З цієї причини для несиметричних Нелін ?? ейностей не можна користуватися рівнянням (12.5), а слід застосовувати рівняння (12.4). Відповідна схема представлена на рис. 12.4, Б.В зв'язку з цим для таких Нелін ?? ейностей замість даються вираження безпосередньо для.
При відсутності зовнішнього впливу і симетричною харак-теристик постійна складова і рівняння (12.4) набирає вигляду:
де - передавальна функція еквівалентного лин ?? ейного ланки, яку можна назвати гармонійною функцією передачі Нелін ?? ейного ланки.
Отже, при гармонійної лин ?? еарізаціі, Нелін ?? ейное ланка замінюється лин ?? ейним, еквівалентним для постійної складової вхідного сигналу і наближено еквівалентним для його коливальної складової. При цьому приблизно приймається, що спектр колебательной складової вхідного сигналу складається з однієї гармоніки, і нехтується її спотворенням в Нелін ?? ейном ланці.
Умовою застосування методу лин ?? еарізаціі в замкнутій системі є виконання лин ?? єйної частиною системи ролі фільтра нижніх частот. Смуга пропускання повинна бути мала в порівнянні з вищими гармоніками автоколебаний.
За допомогою гармонійної лин ?? еарізаціі можна визначити параметри можливих автоколивань в цікавій для нас точці системи, які бувають використані для определ ?? ення стійкості Нелін ?? єйної системи, якості перехідних процесів.