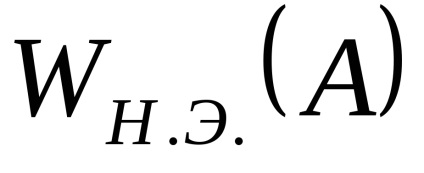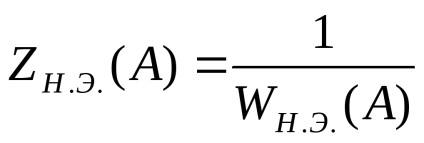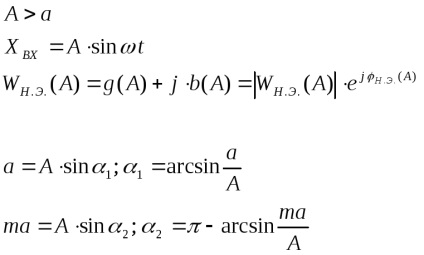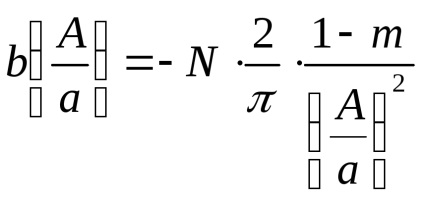Метод гармонійного балансу (гармонійної лінеаризації, метод фільтра)

Попередня ↔ Наступна

Ідея методу полягає в лінеаризації нелінійностей, при цьому коефіцієнти лінеаризації залежать від амплітуди вхідного сигналу, тобто нелінійність замінюється «пучком» лінійно, нахил яких залежить від величини вхідного сигналу. Цей метод досить точний і може бути застосований як до несуттєвих, так і до суттєвих нелінійних (метод Крилова-Боголюбова).

Ідея методу заснована на тому, що лінійні частини багатьох систем мають хороші фільтруючі властивості, тобто є фільтром низьких частот. Такий характеристикою володіють інерційні та інтегрують ланки, АЧХ яких зображені на рис. 2 з яких і складається лінійна частина

Метод гармонійного балансу (гармонійної лінеаризації, метод фільтра)

Якщо розкласти вихідний сигнал нелінійної частини (рис.3) в ряд Фур'є, можна вважати, що лінійна частина пропускає тільки першу гармоніку розкладання і відфільтровує інші, і, отже, на виході лінійної частини залишається гармонійний сигнал. Таким чином, метод гармонійного балансу також є метод лінеаризації, при якому нелінійний сигнал на вході лінійної частини (а значить і на виході нелінійної частини) замінюється лінійним сигналом - першої гармонікою розкладання нелінійного сигналу. Обгрунтованість такої лінеаризації тим вище, чим більшими фільтруючими властивостями володіє лінійна частина.

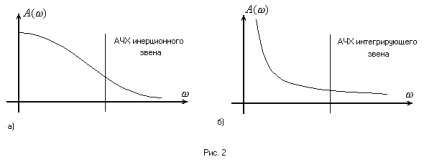
Отже, при гармонійної лінеаризації реальний нелінійний елемент (НЕ) замінюється ідеальним, вихідний сигнал якого дорівнює першій гармоніці розкладання в ряд Фур'є вихідного сигналу реального НЕ.

Завдання гармонійної лінеаризації полягає в тому, щоб визначити еквівалентний комплексний коефіцієнт посилення НЕ (гармонійний коефіцієнт передачі, що описує функція), що представляє комплексний коефіцієнт передачі ідеального НЕ, вихідний сигнал якого представляє першу гармоніку розкладання в ряд Фур'є вихідного сигналу реального НЕ.

Будемо вважати, що на вхід НЕ подається гармонійний сигнал, який є виходом лінійної частини (Рис. 4)

Розкладемо вихідний сигнал н.е. в ряд Фур'є і утримаємо тільки першу гармоніку розкладання (більшість нелинейностей

- непарні).

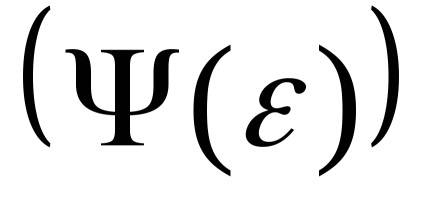
(Тому що функція непарна, то

, друга, четверта і т.д. гармоніки дорівнюють нулю)

- комплексний коефіцієнт передачі нелінійного елемента

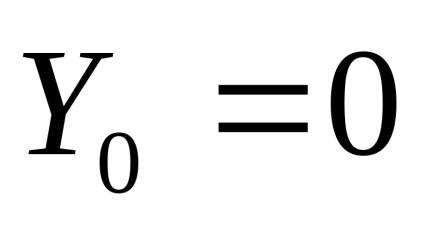
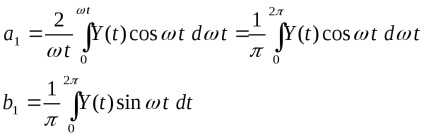
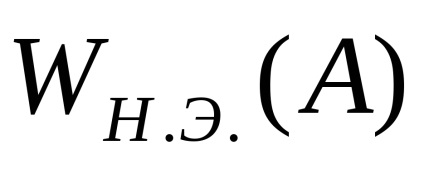
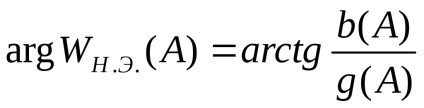
Зауваження: У разі, якщо нелінійність кососімметрічная і не містить неоднозначності, перша гармоніка вихідного сигналу збігається по фазі з вхідним сигналом, тобто не містить косинусоидальной складової, тобто

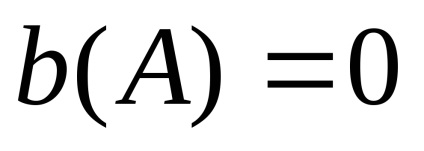
Після лінеаризації рівняння н.е. набуває вигляду:

знайти

, якщо нелінійність має вигляд (Рис. 5)

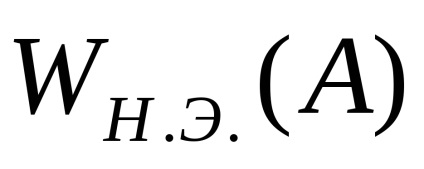
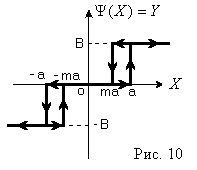
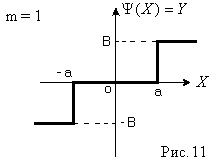
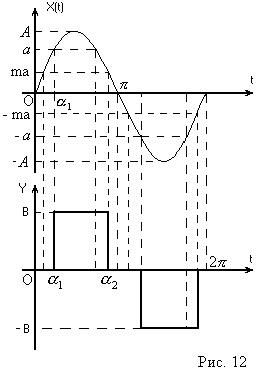
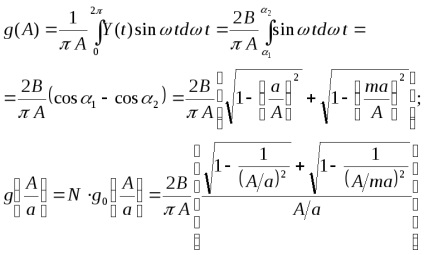
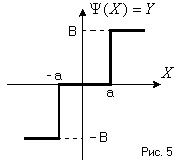
На вхід нелінійного елемента надходить синусоїдальний сигнал, тогдаYбудет гармонійної функцією виду (Рис. 6)

Нелінійність, як видно з рис. 6, кососімметрічна щодо початку координат і не має зони неоднозначності, отже

, а рівняння нелінійного елемента буде мати вигляд:

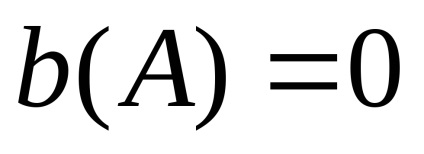
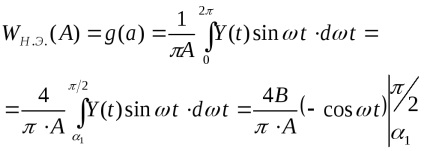
З рис. 6 видно, що при

;

, тоді

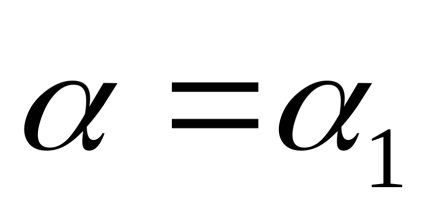
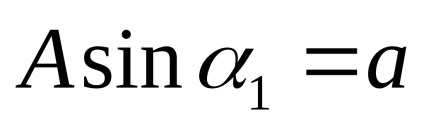
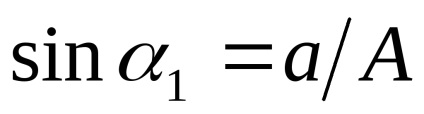
Зручно представити еквівалентний комплексний коефіцієнт посилення в функції безрозмірною амплітуди вхідного сигналу

, тоді

- нормирующий множник, що представляє характеристику нелінійного елемента;

- нормований еквівалентний комплексний коефіцієнт передачі н.е.

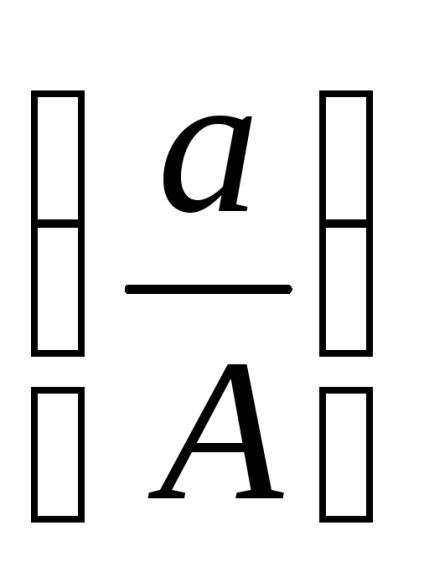
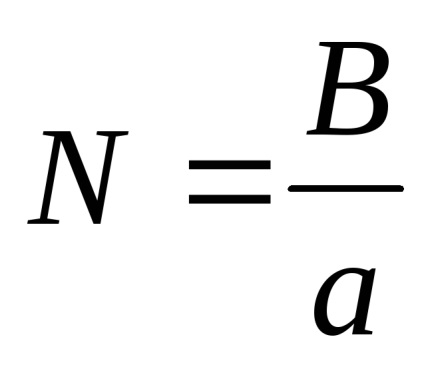
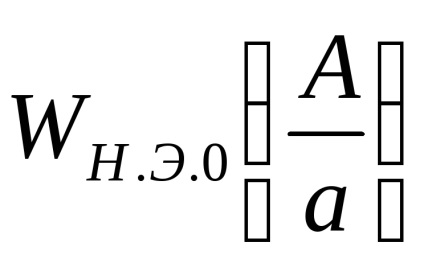
Гідність такого подання в тому, що

залежить тільки від однієї змінної - безрозмірною амплітуди, і його значення можуть бути протабулювати.

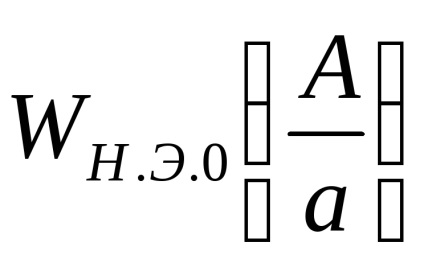
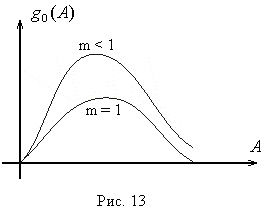
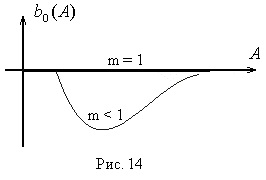
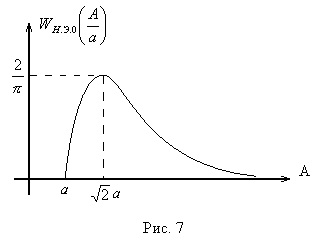
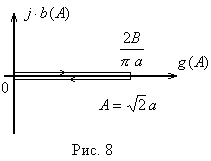
Графік

має вигляд (рис. 7)

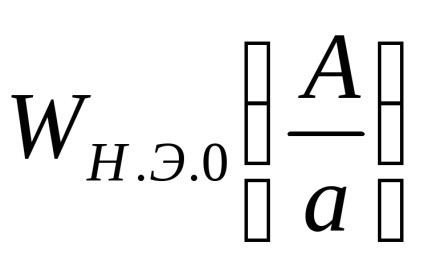
при А <а выходной сигнал нелинейного элемента отсутствует (зона нечувствительности), следовательно

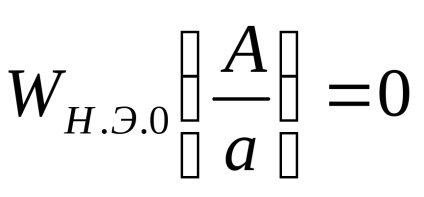
при

вихідний сигнал нелінійного елемента равенB = const, отже,

, тобто залежність має екстремальний характер.

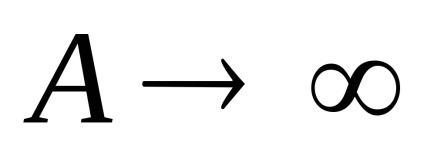
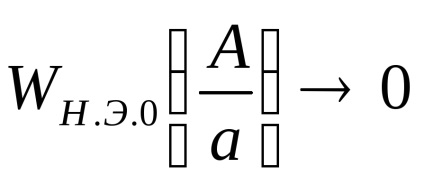
знайдемо екстремум

. позначимо:

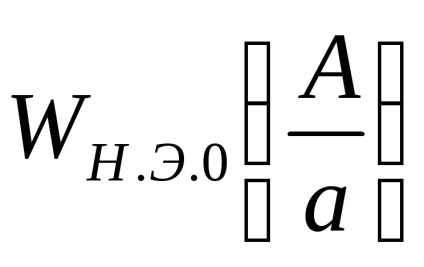
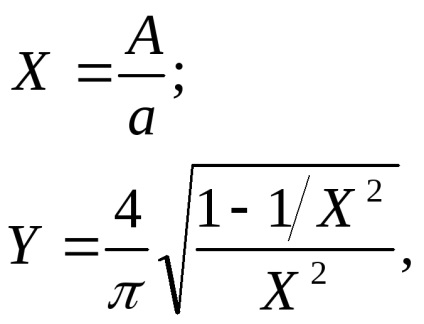
Знайдемо точку екстремуму, тобто значення X, при якому

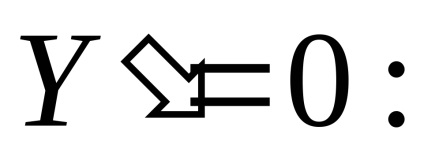
тобто при

маємо екстремум:

;

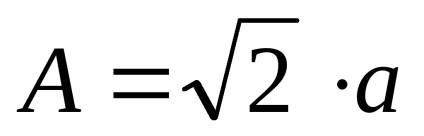
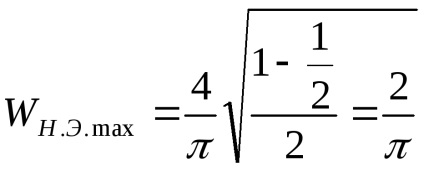
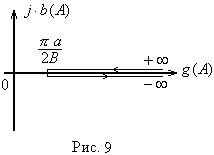
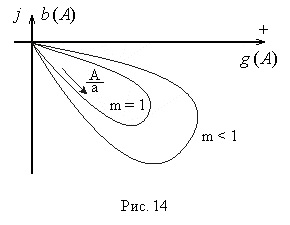
Геометричне місце точок кінця вектора

в комплексній плоскостіпрі зміні амплітуди вхідного сигналу А від 0 до

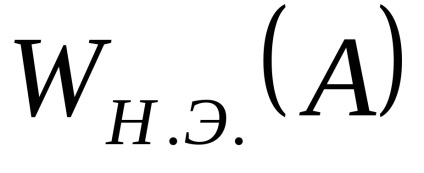
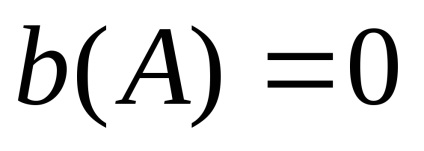
називається годографом еквівалентного комплексного коефіцієнта передачі або амплітудної характеристикою нелінійного елемента. Будується ця характеристика так само, як звичайна АФЧХ, але тільки є функцією амплітуди. В даному прикладі