ідемпотентів півгрупа

ідемпотентна півгрупа, - півгрупа, кожен елемент к-рій є ідемпотентів. І. п. Наз. також зв'язкою (це узгоджується з поняттям зв'язки напівгруп: І. п. є зв'язка одноелементні напівгруп). Коммутативная І. п. Наз. полуструктура, або полурешеткой; цей термін узгоджується з його вживанням в теорії частково впорядкованих множин: якщо комутативну І. п. Sрассмотреть щодо природного часткового порядку, то ab буде найбільшою нижньою гранню елементів Всяка полурешетка є подпрямое твір двоелементний полурешеток. Напівгрупа Sназ. сингулярной, якщо Sудовлетворяет одному з тотожностей ху = х, ху = у, в першому випадку Sназ. левосінгулярной, або полугруппой лівих нулів, в другому - правосінгулярной, або полугруппой правих нулів. Напівгрупа зв. прямокутної, якщо вона задовольняє тотожності хух = х (цей термін використовується іноді і в більш широкому сенсі, см. [1]).

ідемпотентів півгрупа

Наступні умови для напівгрупи S еквівалентні: 1) S прямокутна, 2) Sесть ідеально проста І. п. (Див. Проста півгрупа), 3) Sесть цілком проста півгрупа ідемпотентів, 4) S ізоморфна прямому добутку LR, де L- левосінгулярная, а R- правосінгулярная напівгрупи. Будь-яка І. п. Є кліффордовой полугруппой і розкладається в полурешетку (див. Зв'язка напівгруп) прямокутних напівгруп. Це розкладання служить вихідним пунктом при вивченні багатьох властивостей І. п. Будь-яка І. п. Локально кінцева.

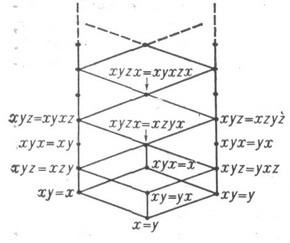
І. п. Вивчалися з різних точок зору, в тому числі з точки зору теорії різноманіть. Решітка всіх підмноговидів різноманіття B всіх І. п. Повністю описана в [4] - [6]; вона Рахункової та дистрибутивного, кожне підмноговидів її може бути задано всередині одним тотожністю. Діаграму цієї решітки см. На рис .; там же вказані тотожності, що задають у різноманіття з декількох нижніх "поверхів".

Літ. : Ll] Кліффорд А. Престон Г. Алгебраїчна теорія напівгруп, пров. з англ. т. 1-2, М. 1972; [2] McLean D., "Amer. Math. Monthly", 1954, v. 61, № 2, p. 110-13; [3] Kimura N. "Pacif. J. Math.", 1958, v. 8, p. 257-75; [4] Бірюков О. П. "Алгебра і логіка", 1970, т. 9, № 3, с. 255-73; [5J Gerhard J. "J. Algebra", 1970, v. 15, № 2, p. 195-224; [6] Fennemоrе З п. "Math. Nachr.", 1971, Bd 48, № 1-6, S. 237-62.

Поділіться на сторінці

  • Брандт Напівгрупа - півгрупа Sс нулем, в якій кожному ненульових елементів асоответствуют такі однозначно певні елементи. що. і для будь-яких двох ненульових ідемпотентів має місце.
  • Гауссова Напівгрупа - комутативна півгрупа з одиницею, яка задовольнить закону скорочення, в якій будь-який необоротний елемент аразложім в твір непріводімих елементів, причому для будь-яких двох таких розкладів має місце k = l і.
  • Інверсний Напівгрупа - півгрупа, в якій для будь-якого елемента асуществует єдиний інверсний до нього елемент а -1.
  • ЛОКАЛЬНО КІНЦЕВА Напівгрупа - півгрупа, в якій кожна звичайно породжена подполугруппа конечна. Будь Л. к. П. Буде періодичної полугруппой. Зворотне невірно: існують навіть периодич. групи, які не є локально кінцевими.
  • Моногенне Напівгрупа - циклічна напівгруп а, - півгрупа, породжена одним елементом. М. п. Породжена елементом о, позначається зазвичай і складається з різноманітних ступенів з натуральними показниками.
  • Нильпотентною Напівгрупа - півгрупа Sс нулем, для якої існує таке п, що.
  • Однопараметричними Напівгрупа - сімейство операторів діючих в банаховому або топологічному векторному просторі X, що володіє властивістю Якщо оператори Tлінейни, обмежені і діють в банаховому просторі X, то з вимірності всіх.
  • ПРОСТА Напівгрупа - півгрупа, яка не містить власних ідеалів або конгруенції того чи іншого фіксованого типу. Залежно від розглянутого твань виникають різні типи П. і. ідеально проста - що не містить.
  • ВІЛЬНА Напівгрупа - над алфавітом А - півгрупа, елементами к-рій. є всілякі кінцеві послідовності елементів з А, а операція полягає в приписуванні однієї послідовності до іншої.
  • Топологічних напівгруп - безліч, наділене алгебраїч. структурою напівгрупи і структурою хаусдорфова топологіч. простору, причому полугрупповая операція неперервна в заданій топології.
  • Впорядкованість Напівгрупа - півгрупа, наділена структурою порядку стабільного щодо полугрупповой операції, т. Е. Для будь-яких елементів а, b, з з слід і Якщо відношення на У. н. Sесть лінійний порядок, то S зв. лінійно.
  • Напівгрупа - одне з основних понять сучасної алгебри. П. називається безліч з визначеною на ньому операцією, підпорядкованої закону асоціативності.

    Велика Радянська Енциклопедія

  • Стислі Напівгрупа - однопараметричними сильно безперервна півгрупа T. Т = I, лінійних операторів в банаховому просторі E, для яких брало.

    Разом. Окремо. Через дефіс. Словник-довідник

    Російський орфографічний словник

    Схожі статті