З виникненням у стародавніх людей здатності рахунку з'явилася необхідність у використанні пристосувань, які змогли б полегшити цю роботу. Одне з таких знарядь праці наших предків було виявлено при розкопках поселення Дольні Вестоніці на південному сході Чехії в Моравії. Звичайна кістка з карбами, що отримала назву «вестоніцкая кістка», використовувалася ними для ведення рахунку імовірно за 30 тис. Років до н.е.
Різні стародавні цивілізації довгий час використовували такий спосіб для запису чисел. Так, наприклад, за 2 тис. Років до н.е. на колінах статуї шумерського царя гуде висічено лінійка, поділена на шістнадцять рівних частин. Одна з цих частин була в свою чергу поділена на дві, друга на три, третя на чотири, четверта на п'ять, а п'ятий на шість рівних частин. Причому в п'ятій частині довжина поділів становила 1 мм.
Приблизно до VIII століття до н.е. древніми індійськими цивілізаціями був придуманий інший спосіб для запису чисел. Для цих цілей вони використовували вузликове письмо, в якому знаками служили камені і різнокольорові мушлі, сплетені разом мотузками.
Розвиток держав Європи та Азії, а також посилення торговельних відносин між ними призвело до створення цілком нового інструменту, відомого практично у всіх народів. Вперше його почали застосовувати у Вавилоні, а незабаром новий винахід потрапило до Греції, де отримало свій подальший розвиток. Це пристосування являло собою дерев'яну дощечку, посипану морським піском, на якому наносилися борозенки. Розміщення в цих борозенках камінчики позначали цифри. При цьому кількість камінців у першій борозенці відповідало одиниць, у другій - десяткам, в третій - сотням і т.д. Якщо в одній з борозенок набиралося десять камінчиків, то їх знімали і додавали один камінчик в наступну борозенку.

Трохи пізніше замість дерев'яних дощечок стали використовувати кам'яні плити з виточеними в них жолобками. Одна з таких плит була виявлена на острові Саламін в Егейському морі в 1899 році. «Саламинського дошка», довжиною півтора метра і шириною трохи більш сімдесяти сантиметрів, була виготовлена приблизно за 300 років до н.е. На цій мармуровій плиті в лівій її частині було нанесено одинадцять вертикальних ліній, розділених горизонтальною лінією, таким чином, що вони утворювали десять стовпців. У правій частині також було прорізано п'ять вертикальних ліній, які, в свою чергу, утворювали чотири стовпці. По периметру плити були також викарбувані літери грецького алфавіту.
У Стародавньому Римі «Саламинського дошка» з'явилася, ймовірно, в V-VI ст н.е. і називалася вона calculi або abakuli. Для виготовлення римського абака, крім кам'яних плит, стали використовувати бронзу, слонову кістку і навіть кольорове скло. У вертикальних желобках, розділених на два поля, також містилися камінці або мармурові кульки, при цьому жолобки нижнього поля служили для рахунку від одиниці до п'яти. Якщо в цьому жолобки набиралося п'ять кульок, то в верхнє відділення додавався один кулька, а з нижнього поля всі кульки знімали.
Суан-пан - китайська різновид абака - з'явилася в VI столітті н.е. У XII-XIII століттях він придбав свою класичну форму, яка дійшла до наших днів. Суан-пан являє собою прямокутну раму з натягнутими паралельно один одному дев'ятьма або більше нитками. Також як і римський абак, Суан-пан розділений на два поля, що мають свої назви. Більша поле називається «Земля», а менше - «Небо». У більшому поле на кожній мотузці нанизано по п'ять кульок, а в меншому за все по два. При підрахунку кульки вже не знімаються з поля, вони лише пересуваються в сторону сусіднього поля. Кожен кульку більшого поля відповідає одиниці, а кожен кульку меншого поля - п'яти.
З Китаю суан-пан в XV-XVI століттях був завезений до Японії. Від нього стався соробан, який остаточно сформувався тільки в тридцяті роки XX століття. Соробан відрізняється від свого попередника меншою кількістю кульок в кожному полі. Так, в меншому полі всього одну кульку замість двох, а в нижньому - чотири замість п'яти.
Приблизно в X-XI століттях на іншому континенті цивілізацією Ацтеків була придумана своя різновид абака. Вони його назвали «nepohualtzitzin». Крізь дерев'яний каркас були протягнуті нитки, на яких нанизувалися зерна кукурудзи. Каркас був розділений на два поля, в одному з яких на кожній нитки розміщувалося по три зерна, а в іншому - по чотири. Для роботи з таким інструментом використовувалася своя особлива система рахунки
Поширюючись в європейських країнах, римський абак поступово видозмінювався. У XV столітті в Англії з'явилася нова його форма, яка називається «лінійчатої дошкою» (line-board).

Приблизно в цей же час на Русі набув поширення так званий «дощатий рахунок», завезений, мабуть, купцями з Європи. Він представляв собою рамку з укріпленими горизонтальними мотузками, на які були нанизані просвердлені сливові або вишневі кісточки. Ця рамка розбивалася спочатку на чотири, а потім на два рахункових поля. У 1658 році в «переписних книг ділової казни Патріарха Никона» замість «дощатий рахунок» вживається слово «рахунки». А на початку XVIII століття рахунки взяли свій звичний вигляд, який в подальшому не зазнавав суттєвих змін. У них залишилося лише одне рахункове поле, на спицях якого розміщувалося по десять кісточок.
Після винаходу абака людська думка не стояла на місці. Багато винахідників і натуралісти намагалися придумати пристосування, здатні полегшити процес обчислень.
У 1617 році Шотландський математик Джон Непер (John Naiper, 1550-1617) запропонував інструмент, який отримав назву «рахункові палички Непера». Вони виконувалися у вигляді прямокутних брусків, розділених на десять квадратів. Кожен квадрат, в свою чергу, крім самого верхнього, ділився по діагоналі на дві частини, в кожній з яких в певному порядку записувалися числа. Самий верхній квадрат містив лише одну цифру. Крім цього в набір входив ще один брусок, поділений також на десять частин. Верхній квадрат такого бруска залишався порожнім, а в нижні записувалися по порядку числа від одиниці до дев'яти.

Для виконання операції множення двох чисел брався основний брусок і брусок, у якого в верхньому квадраті був записаний один з множників. Далі ці бруски розташовувалися поряд так, щоб їх краї збігалися. Після цього в тому квадраті, який розташовувався на одній лінії з другим множником, з основного бруска складалися два знаходилися там числа, при цьому число, яке розташовувалося лівіше, позначало десятки, а число правіше - одиниці. Таким чином, операція множення зводилася до складання.
Приблизно в 1650 році, через майже сорок років після відкриття Джоном Непер логарифмів, англійці Роберт Біссакар, а в 1657 році - незалежно від нього - С. Патрідж винайшли логарифмічну лінійку - пристрій, що дозволяє значно прискорити процес обчислення. Шкала на логарифмічною лінійці розмічається за допомогою таблиць логарифмів. Робота логарифмічною лінійки грунтувалася на властивостях логарифмів - для множення двох чисел досить скласти їх логарифми. Завдяки цій властивості, складна операція множення зводиться до простої операції додавання.
Лінійка Ватта - перша універсальна логарифмічна лінійка, придатна для виконання будь-яких інженерних розрахунків, була сконструйована в 1779 році видатним англійським механіком Джоном Ватто. Вона отримала назву «Сохо-лінійки», по імені містечка поблизу Бірмінгема, де працював Ватт.
В кінці XIX століття офіцером французької армії Амеді Маннхеімом (1831-1906) була розроблена кругла логарифмічна лінійка, обчислення на якій відрізнялися більшою точністю, ніж на звичайній прямий лінійці.
Незважаючи на гадану, на перший погляд простоту, практично всі перші інструменти для роботи з числами не тільки дожили до наших днів, але подекуди використовуються досі.
Одна з найперших спроб створення механічної лічильної машини, ймовірно, належить великому італійському художнику, скульптору і винахіднику епохи Відродження Леонардо да Вінчі (1452-1519). Серед двотомного зібрання рукописів відомих як «Codex Madrid» і майже повністю присвячених механіки, були виявлені креслення і опис такого пристрою. Схожі малюнки також були знайдені і в рукописах «Codex Atlanticus».
Історія цього проекту знайшла своє продовження в XX столітті. Саме тоді в 1968 році, за ескізами Леонардо да Вінчі, було побудовано і продемонстровано пристрій, що підсумовує.
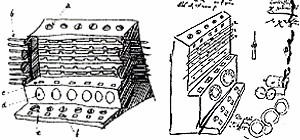
Дотримуючись описами і кресленнями, наведеними в листах, можна припустити наступне. До кожного з шести основних стрижнів, розташованих в один ряд, з зовнішньої сторони машини кріпився диск для установки чисел. До нього зсередини кріпилася шестерня з десятьма зубами. На бічну поверхню цієї шестерні наносилися цифри від нуля до дев'яти, які були видні в спеціальному віконці. І, нарешті, на цьому ж стержні кріпилося спеціальне колесо з одним зубцем. Його роль зводилася до того, що при повному обороті перший стрижня це колесо повертало сусідній стрижень лише на десяту частину. Зв'язок між сусідніми стрижнями здійснювалася за рахунок проміжного колеса з десятьма зубцями, яке необхідно було, для того щоб всі основні стрижні оберталися в одну сторону. Таким чином, проводилися операції додавання і віднімання. Крім цього передбачалося використовувати спеціальні палички Напье циліндричної форми, які б вставлялися в верхню частину машини. З їх допомогою можна було б виконувати також і множення.
Воістину титанічна праця виконав видатний математик, фізик, винахідник і механік Блез Паскаль (Blaise Pascal, 1623-1662) для створення машини, за допомогою якої можна було проводити арифметичні операції. За час роботи над пристроєм, Паскалем було зроблено більше п'ятдесяти різних моделей, в яких винахідник експериментував не тільки з матеріалом, але і з формою деталей машини.
Перша працює машини була виготовлена вже в 1642 році, але остаточний варіант арифметичної машини або "колеса Паскаля" з'явився тільки до 1645 році. Вона представляла собою легкий латунний скриньку розміром 350x125х75 мм. На верхній кришці було зроблено вісім круглих отворів, навколо кожного нанесена кругова шкала. Шкала крайнього правого отвори розділена на дванадцять рівних частин, шкала сусіднього з ним отвори - на двадцять частин, шкали інших шести отворів мають десяткове поділ.
Така градуювання використовувалася з наступних причин. Паскаль створював машину в допомогу своєму батькові, який був збирачем податків. Отже, за основу він поклав систему рахунку французької валюти того часу. Основною грошовою одиницею тоді був лівр, який дорівнював двадцяти су. Су, в свою чергу складався з дванадцяти деньє.
В отворах розташовувалися зубчасті колеса. Число зубів кожного колеса дорівнювало числу поділок шкали відповідного отвору. Так, у крайнього правого колеса дванадцять зубів, у сусіднього - двадцять, в інших по десять. Також у кожній шестірні був один подовжений зубець, який при повному повороті колеса повертав сусіднє колесо. Так при дванадцяти повних поворотів крайнього правого колеса за рахунок цього зубця сусіднє колесо здійснювало один повний поворот. Поворот колеса передається за допомогою внутрішнього механізму машини циліндричному барабану, вісь якого розташовувалася горизонтально. Один поворот зубчастого колеса відповідав однієї операції додавання. На бічній поверхні барабана були нанесені цифри від нуля до дев'яти, які були видні в прямокутних вікнах кришки. У цих вікнах виводився результат арифметичної операції. Також як і в машині Шиккарда, для того щоб зубчасті колеса оберталися в одну сторону, вони з'єднувалися за допомогою додаткової проміжної шестерні, але на противагу «рахункових годинах», колеса пересувалися тільки за годинниковою стрілкою і були призначені лише для складання чисел. Віднімання можна було виконати, застосовуючи досить громіздку методику.
Протягом наступних тридцяти років після винаходу Паскаля, багато хто намагався створити свій варіант обчислювальної машини, спираючись на цей проект. Найбільш відомою з цього числа була рахункова машина англійця Семюеля Морланда (Samuel Morland, 1625-1695). Винайдена в 1666 році вона використовувала Дванадцяткова шкалу, яка грунтувалася на системі рахунку англійських грошових одиниць.