На рис. 52 представлені ізотерми газу Ван-дер-Ваальса.
При дуже високих температурах вони мають форму, близьку до гіпербол; ці ізотерми характеризують газоподібний стан речовини (майже ідеальний газ). У міру зменшення температури форма ізотерми змінюється і при деякій температурі (критична) виявляє точку перегину кривої. При ще менших температурах (докритичних) ізотерми замість горизонтальної ділянки, відповідного фазового переходу рідина - пар, мають хвилеподібний ділянку (рис. 53).
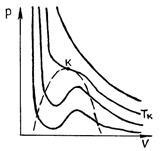
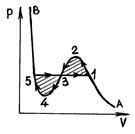
Мал. 52 Р і с. 53
Вимірювання показують, що ізотерми реального речовини практично збігаються з ізотермою Ван-дер-Ваальса на ділянках (газоподібний стан) і (рідкий стан). Однак в середній частині замість горизонтальної ділянки 51, відповідного фазового переходу рідина - пар, ізотерма Ван-дер-Ваальса має хвилеподібний ділянку. Цей хвилеподібний ділянку характеризується наступним чином. Ділянка 12 відповідає метастабильному стану пара (пересичений пар), а ділянка 54 - метастабильному стану рідини (перегріта рідина). У точці 1 є тільки насичений пар, а в точці 5 - тільки кипляча рідина. Що стосується ділянки 234 хвилеподібною кривою, то він фізично неможливий, так як в природі немає речовин, для яких при постійній температурі збільшення обсягу призводило б до зростання тиску. Останнє можливе лише в разі, якщо на цій ділянці температура не є постійною. Пересичена пара (ділянка 12) - газоподібний стан речовини, в якому тиск p більше, ніж тиск насиченої пари при даній температурі - можна на досвіді отримати, стискаючи чистий газ до тиску, більшого тиску насичених парів, і він не буде конденсуватися. Стан пересичені пара, хоча і володіє певною стійкістю, але воно менш стійко, ніж двофазне стан (ізобара 135), при якому, як ми знаємо, частина речовини знаходиться в вигляді рідини, а частина - у вигляді насиченої пари. Тому при невеликому зовнішньому впливі пересичена пара частково переходить в рідину, а залишився пар стає насиченим.
Перегріту рідину (ділянка 45) - стан, що характеризується тим, що воно існує при тиску нижчому, ніж тиск насиченої пари при даній температурі - можна отримати при тривалому кип'ятінні чистої рідини, в результаті чого з рідини видаляються газові бульбашки (центри пароутворення), і рідина нагрівається до температури вище температури кипіння при даному тиску. Стан перегрітої рідини також виявляється менш стійким, ніж стан рівноваги між рідиною і насиченою парою. Якщо в таку перегріту рідину ввести частки стороннього речовини, то відбувається швидкий перехід її в двофазне стан.
Стану пересичені пара і перегрітої рідини використовуються в приладах ядерної фізики (камера Вільсона і бульбашкова камера) для реєстрації та вимірювання параметрів елементарних частинок.
Якщо на изотерме Ван-дер-Ваальса хвилеподібний ділянку замінити деякою горизонтальної прямої 135, то отримана так ізотерма буде якісно правильно описувати та двофазне стан речовини. Положення цієї прямої можна визначити, якщо до замкнутого оборотного циклу 1234531 застосувати другий початок термодинаміки в запису Клаузиуса (2.13.7):
Оскільки вздовж усього шляху 1234531 температура речовини залишається незмінною (бо цей шлях складений з ділянок двох можливих варіантів однієї і тієї ж ізотерми), то останнє рівняння може бути записано у вигляді
Підставляючи в це співвідношення значення з першого закону термодинаміки і враховуючи, що
отримуємо для розглянутого циклу:
Проробимо з останнім рівністю очевидні перетворення
т. е. горизонтальну пряму 135 потрібно провести так, щоб заштриховані на рис. 53 площі були рівні.
Як було вже зазначено, в критичній точці ізотерма має дотичну і перегин, тому в цій точці повинні виконуватися співвідношення
де запис означає, що відповідні похідні обчислюються при значеннях параметрів речовини, рівним критичним. Записавши рівняння Ван-дер-Ваальса у вигляді
обчисливши потім похідні і, прирівнявши їх до нуля, неважко отримати
З виразів (3.6.8-3.6.10) слід, що співвідношення
не залежить від природи речовини. Досвід же показує, що величина має різні значення для різних газів: для водню вона дорівнює 0,33, для кисню - 0,29, для вуглекислого газу - 0,22. Ці істотні розбіжності величини з експериментальними даними свідчать, що рівняння Ван-дер-Ваальса, з якого ця величина отримана, є наближеним, хоча якісна картина зміни стану речовини передається рівнянням досить правильно. Відома велика кількість спроб отримання більш точного рівняння стану речовини. Однак ці рівняння містять велику кількість поправочних коефіцієнтів, фізичний зміст яких незрозумілий, як в рівнянні Ван-дер-Ваальса.
У найбільш загальному вигляді методами статистичної фізики академіком Н. Н. Боголюбовим отримано рівняння стану
де - так звані коефіцієнти віриалів, які є функціями тільки температури. З рівняння Боголюбова слід, що чим більше значення молярного об'єму. тим менше число членів ряду слід враховувати для отримання достатньо точного результату. При всі члени степеневого ряду звертаються в нуль, і рівняння (3.6.12) набуває вигляду. т. е. як і слід було очікувати, рівняння Боголюбова перетворюється в рівняння Менделєєва - Клапейрона. Коефіцієнти віриалів не можуть бути обчислені чисто теоретичними методами і тому повинні визначатися за допомогою експериментальних даних. Однак це завдання виявляється настільки складною, що більш доцільним є отримання рівняння стану просто у вигляді інтерполяційної формули, яка описує експериментальні дані.