Як спрощувати складові дроби

Складова дріб - це дріб, у якої в чисельнику або в знаменнику або і в чисельнику, і в знаменнику знаходиться дріб. З цієї причини складові дробу ще називають багатоповерховими дробом. Процес спрощення складових дробів варіюється від простого до складного - в залежності від числа членів виразів, які перебувають в чисельнику і в знаменнику, або від наявності змінних в чисельнику і в знаменнику.

кроки Правити

Метод 1 з 2:
Спрощення складових дробів через множення на зворотну величину Правити

При необхідності спростите і чисельник, і знаменник до однієї звичайного дробу. Легко спростити складову дріб, у якої і в чисельнику, і в знаменнику знаходиться одна звичайна дріб. Тому, якщо в чисельнику або в знаменнику даної вам складовою дробу знаходяться кілька дробів або дроби і цілі числа, спростите їх, щоб отримати по одній дроби і в чисельнику, і в знаменнику. Для цього буде потрібно знайти найменший спільний знаменник (НСЗ).

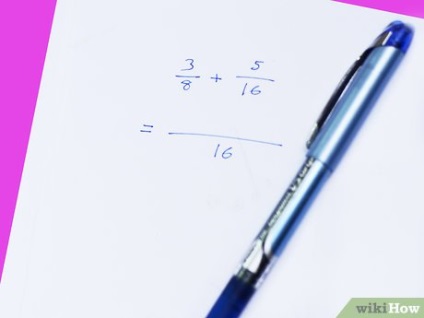
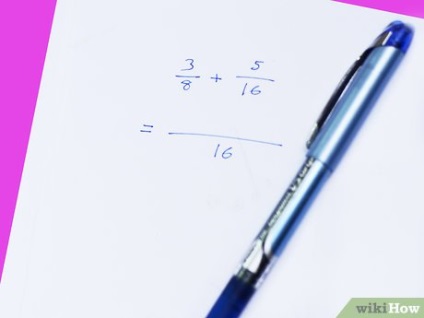
• Наприклад, дана складова дріб: (3/5 + 2/15) / (5/7 - 3/10). По-перше, спростимо і чисельник, і знаменник цього дробу до однієї дробу.
  • Для дробів, що знаходяться в чисельнику, НСЗ = 15. Тому наведемо дріб 3/5 до спільного знаменника: 3/5 * 3/3 = 9/15. Перепишемо чисельник як: 9/15 + 2/15 = 11/15.
  • Для дробів, що знаходяться в знаменнику, НСЗ = 70. Тому наведемо обидві дроби до спільного знаменника: 5/7 * 10/10 = 50/70 і 3/10 * 7/7 = 21/70. Перепишемо знаменник як: 50/70 - 21/70 = 29/70.
  • Таким чином, перепишемо складову дріб як: (11/15) / (29/70).

Для отримання зворотного дробу поміняйте місцями чисельник і знаменник. Правило: розподіл першого числа на друге одно множенню першого числа на зворотну величину другого числа. Тепер, коли і в чисельнику, і в знаменнику складовою дробу знаходиться по одній дробу, можна скористатися цим правилом для спрощення складовою дробу. По-перше, знайдіть зворотну дріб для дробу, що знаходиться в знаменнику складної дробу. Для цього поміняйте місцями чисельник і знаменник дробу.

• У нашому прикладі дріб в знаменнику - це 29/70. Зворотній їй дріб - це 70/29.
  • Зверніть увагу, що якщо в знаменнику складовою дробу знаходиться ціле число, то його зворотна величина знаходиться за тими ж правилами. Наприклад, якщо дана складова дріб (11/15) / (29), то зворотна величина цілого числа 29 (його можна записати як дріб 29/1) є дріб 1/29.

Перемножте дві дробу. Помножте дріб, що знаходиться в чисельнику складовою дробу, на отриману зворотний дріб. Для цього окремо перемножте їх чисельники і окремо - знаменники.

• У нашому прикладі: 11/15 * 70/29. 11 * 70 = 770 і 15 * 29 = 435. Отже, результат множення: 770/435.

Спростіть отриману дріб, знайшовши найбільший спільний дільник (НСД). НСД - це найбільше число, на яке діляться і чисельник, і знаменник. Знайдіть НСД і розділіть на нього і чисельник, і знаменник.

• У нашому прикладі НОД = 5. Таким чином, 770/5 = 154 і 435/5 = 87. Спрощена дріб (і остаточну відповідь): 154/87.

По можливості використовуйте правило множення на зворотну величину (наведене вище). Чисельник і знаменник практично будь-якої складової дробу може бути спрощений до однієї дробу. Складові дробу, що містять змінну, не є винятком; однак, чим складніше вираз зі змінною, тим складніше його спростити. У разі складних виразів зі змінною (що містять кілька членів) скористайтеся методами спрощення, описаними нижче.

• Наприклад, складову дріб (1 / х) / (х / 6) легко спростити через множення на зворотну величину: (1 / х) * (6 / г) = 6 / х 2.
• Інший приклад: дріб (((1) / (x + 3)) + x - 10) / (x +4 + ((1) / (x - 5))) важко спростити через множення на зворотну величину. Тобто вираження в чисельнику і в знаменнику буде складно спростити до однієї дробу. Тому скористайтеся методами спрощення, описаними нижче.

Почніть з пошуку найменшого спільного знаменника дробів, що знаходяться і в чисельнику, і в знаменнику складовою дробу. Для цього, як правило, просто перемножте знаменники цих дробів.

• Це легше зрозуміти на прикладі. Спробуємо спростити складову дріб: (((1) / (x + 3)) + x - 10) / (x +4 + ((1) / (x - 5))). У цій складовою дробу є дроби (1) / (х +3) і (1) / (х-5). Їх найменший спільний знаменник (НСЗ) дорівнює (х +3) (х-5).

Помножте і чисельник, і знаменник складовою дробу на знайдений НСЗ. Іншими словами, ви помножите складову дріб на НСЗ / НСЗ (тобто на 1, що не впливає на вихідне значення дробу).

• У нашому прикладі ви помножите складову дріб (((1) / (х +3)) + х - 10) / (х +4 + ((1) / (х - 5))) на ((х +3) ( х-5)) / ((х +3) (х-5)).
• Помножте чисельник: (((1) / (x + 3)) + x - 10) × (x + 3) (x-5)
  • = (((X + 3) (x-5) / (x + 3)) + x ((x + 3) (x-5)) - 10 ((x + 3) (x-5))
  • = (X-5) + (x (x 2 - 2x - 15)) - (10 (x 2 - 2x - 15))
  • = (X-5) + (x 3 - 2x 2 - 15x) - (10x 2 - 20x - 150)
  • = (X-5) + x 3 - 12x 2 + 5x + 150
  • = X 3 - 12x 2 + 6x + 145

Помножте знаменник так само, як ви помножили чисельник.

• Помножте знаменник: (x +4 + ((1) / (x - 5))) × (x + 3) (x-5)
  • = X ((x + 3) (x-5)) + 4 ((x + 3) (x-5)) + (1 / (x-5)) (x + 3) (x-5).
  • = X (x 2 - 2x - 15) + 4 (x 2 - 2x - 15) + ((x + 3) (x-5)) / (x-5)
  • = X 3 - 2x 2 - 15x + 4x 2 - 8x - 60 + (x + 3)
  • = X 3 + 2x 2 - 23x - 60 + (x + 3)
  • = X 3 + 2x 2 - 22x - 57

Запишіть нову спрощену дріб. Після множення вихідної складовою дробу на НСЗ / НСЗ і приведення подібних членів ви отримаєте звичайну дріб. Таким чином, помноживши на НСЗ вихідну складову дріб, ви позбулися дробів і в чисельнику, і знаменнику, в яких тепер знаходяться тільки цілі числа і змінні.

• Отже, в чисельник запишіть вираз: x 3 - 12x 2 + 6x + 145, а в знаменник - вираз: x 3 + 2x 2 - 22x - 57. Спрощена дріб: (x 3 - 12x 2 + 6x + 145) / (x 3 + 2x 2 - 22x - 57)

Схожі статті

• Правильні і неправильні дроби »

• Розподіл десяткового дробу на натуральне число

• Які номери дробу краще на полюванні на гусака, які патрони використовувати, правила випередження стрільби