Кодом Хеммінга називається (n, k) - код, який задається матрицею перевірок H (n, k). має рядків і стовпців, причому стовпцями H (n, k) є все різні ненульові виконавчі послідовності довжини m (m - розрядні двійкові числа від 1 до).
Довжина кодової комбінації коду Хеммінга дорівнює.
Число інформаційних елементів визначається як.
Отже, код Хеммінга повністю задається числом m - кількістю перевірочних елементів в кодової комбінації.
Знаючи вид матриці H (n, k). можна визначити коригувальні властивості (n, k) - коду Хеммінга. Так як всі стовпці матриці перевірок різні, то ніякі два стовпці H (n, k) не є лінійно залежними. Поряд з цим, для будь-якого числа m завжди можна вказати три стовпці матриці H (n, k). які лінійно залежні, наприклад, стовпці, що відповідають числам 1, 2, 3. Отже, для будь-якого (n, k) - коду Хеммінга dmin = 3.
Код Хеммінга є одним з нечисленних прикладів досконалого коду.
Дійсно, оскільки (n, k) - код Хеммінга виправляє все поодинокі помилки, то всі зразки одиночних помилок (а їх всього налічується варіантів) повинні розміститися в різних суміжних класах, число яких також дорівнює. Отже, крім суміжних класів, що містять зразки одиночних помилок, ніяких інших в таблиці декодування немає, що і підтверджує досконалість коду Хеммінга.
При фіксованому числі можна побудувати код Хеммінга будь-якої довжини () шляхом укорочення (n, k) - коду. Скорочення не применшує мінімальна кодова відстань. В силу того, що для будь-якого числа n існує код Хеммінга, будь груповий код з виправленням одиночних помилок прийнято називати кодом Хеммінга.
Приклад 5.13. Визначимо параметри кодів Хеммінга природної довжини для різних значень m. Результати представимо у вигляді таблиці.
Очевидно, що мінімальна довжина коду Хеммінга, що має практичне значення, є 3. При збільшенні n відношення зростає і прагне до 1.
Приклад 5.14. Розглянемо код Хеммінга (7,4). Матриця перевірок цього коду складається з 7 Трехразрядное двійкових чисел від 1 до 7:
З розгляду цієї матриці видно, що мінімальне число лінійно залежних стовпців дорівнює 3 (до прикладу 1, 2 і 3), отже, dmin = 3.
У тому випадку, коли стовпчики матриці H (n, k) - коду Хеммінга є упорядкована запис m - розрядних двійкових чисел, декодування здійснюється оригінальним чином. В результаті обчислення перевірочного співвідношення для кодової комбінації, має одиночну помилку, виходить синдром в точності рівний номеру елемента, в якому сталася помилка.
Дійсно, якщо ei містить одну одиницю в розряді, відповідному помилкового елементу, то при множенні на матрицю Н Т всі рядки матриці Н Т. відповідні нулях в ei. звертаються в нулі, і лише рядок, відповідна "1" в ei зберігає свій вигляд (тобто порядковий номер елемента в двійковій запису) у відповіді.
Приклад 5.15. Нехай приймач УЗО системи передачі даних зареєстрував комбінацію. Обчислення синдрому дає
тобто помилка в четвертому елементі і кодова комбінація коду (7,4), яка була передана, має вигляд:
Шляхом нескладних перетворень з (n, k) - коду Хеммінга з dmin = 3 можна отримати (n +1, k) - код Хеммінга з dmin = 4.
Для цього в кодову комбінацію вводиться надлишковий елемент, який є результатом перевірки на парність по всіх елементах кодової комбінації. Число інформаційних елементів залишається тим самим.
Матриця перевірок для (n +1, k) - коду Хеммінга з dmin = 4 виходить з матриці перевірок (n, k) - коду з dmin = 3 шляхом введення додаткової рядки з (n +1) -го одиниці.
Так як розмірність матриці перевірок коду з dmin = 4 має дорівнювати, то до кожного рядка матриці перевірок коду з dmin = 3, необхідно додати один нульовий елемент для того, щоб не порушити введені раніше перевірки. Матриця перевірок для (n +1, k) - коду dmin = 4 має вигляд:
Розглянута процедура, яка призвела до подовження кодової комбінації на один розряд при збільшенні dmin на 1 одиницю, отримала назву подовження коду (1 подовження) .Подовження можуть бути піддані і інші коди, наприклад, коди Ріда-Соломона.
Приклад 5.16. Побудувати код Хеммінга (8,4) з dmin = 4 на основі матриці перевірок коду (7,4).
По виду матриці можна зробити висновок про те, що в коді (7,4) здійснюється 3 незалежні перевірки на парність.
Кожний з рядків визначає елементи кодової комбінації, охоплені однією перевіркою.
Таким чином, матриці відповідає наступна система перевірочних співвідношень:
Для того, щоб отримати код (8,4) з dmin = 4 вводимо ще одну перевірку по всіх елементах кодової комбінації, а результат цієї перевірки записується у вигляді додаткового 8-го елемента:
Цією перевірці відповідає додаткова (четверта) рядок в матриці Н (8,4). що складається з восьми одиниць. Для того щоб не порушити три попередні перевірки на місці восьмого елемента в трьох перших рядках матриці Н (8,4) на місці восьмого елемента, проставляємо нулі. Отже, матриця перевірок коду (8,4) отримана у вигляді:
Визначимо відомим способом dmin (8,4) - коду. З розгляду тих стовпців, сума яких давала нульовий стовпець в (7,4) - коді, видно, що з додаванням 4-ої рядка вони перестали бути лінійно залежними. Тепер вже число лінійно залежних стовпців має бути парним і мінімум 4, наприклад, 3 перші шпальти і останній. Таким чином, для отриманого коду Хеммінга (8,4) dmin = 4.
До сих пір ми ще не розділили елементи кодової комбінації на інформаційні та перевірочні. Найбільш раціонально, по-видимому, це можна зробити наступним чином. Бажано, щоб кожне перевірочне співвідношення однозначно визначало перевірки елемент як результат перевірки на парність деякої сукупності інформаційних елементів. В такому випадку ми отримали б можливість визначати значення перевірочного елемента найбільш простим чином - рішенням одного лінійного рівняння з одним невідомим. Для цього при впорядкованої записи стовпців матриці H (n, k) в якості перевірочних елементів необхідно брати елементи з номерами 2 i. де i змінюється від 0 до m -1, так як саме ці стовпці містять тільки по одній одиниці. Останнє свідчить про те, що елементи з номерами 2 i входять тільки в одну перевірку і, отже, вони можуть бути взяті в якості перевірочних.
Приклад 5.17. Визначити місце розташування перевірочних елементів до коді Хеммінга (7,4).
По виду матриці, наведеної в попередньому прикладі, як перевірочних елементів вибираємо елементи, яким відповідають стовпці, що містять тільки по одній одиниці, тобто перший, другий і четвертий. Отже, 4 інформаційних елемента коду (7,4) повинні займати місця 3, 5, 6 і 7-го розрядів. Наведена в попередньому прикладі система перевірочних співвідношень дозволяє визначити значення кожного з перевірочних елементів за значеннями інформаційних елементів, тобто за значенням елементів простого коду, який необхідно закодувати кодом Хеммінга
Знаючи місця перевірочних елементів, легко привести матрицю H (n, k) коду Хеммінга до канонічної формі.
Для цього необхідно стовпці з номерами 2 i. де при впорядкованої записи стовпців перемістити на місця m перших шпальт в порядку убування номерів. У загальному вигляді така перестановка стовпців в матриці H (n, k) призводить до еквівалентного (n, k) - коду. У разі ж кодів Хеммінга природної довжини код виходить навіть не еквівалентний, а в точності збігається з вихідним кодом.
Приклад 5.18. Перетворити матрицю до канонічної формі.
Переставимо стовпці: 4-ий на місце 1-го, 1-ий на місце 3-го, а 3-ий на місце 4-го:
Це і є канонічна форма матриці. Порівняння її з вихідною матрицею показує, що місцях інформаційних елементів в канонічній формі відповідають стовпці з номерами 3, 5, 6, 7, а місцях перевірочних елементів - стовпці 4, 2, 1.
При цьому зв'язку між інформаційними і надлишковими елементами збереглися з урахуванням їх перестановки:
Породжує матрицю G (n, k) для коду Хеммінга можна отримати з матриці H (n, k). використовуючи теорему 5.3:
Кодують і декодуючі пристрої для цього класу кодів будуть розглянуті при вивченні циклічних кодів.
Оцінимо ефективність кодів Хеммінга.
а) Коди Хеммінга з dmin = 3
Такі коди використовуються або для виправлення помилки кратності t = 1, або для гарантійного виявлення помилок кратності S = 2. Відповідно, ймовірність помилки для цих випадків в каналі з групуванням помилок дорівнює:
Виграш за достовірності порівняно з простими кодами тієї ж довжини становить:
Для таких кодів можливі два режими - виправлення одноразових помилок і виявлення помилок і тільки виявлення помилок. Імовірність помилки для цих режимів в разі групування помилок дорівнює:
Виграш за достовірності порівняно з простим кодом тієї ж довжини становить:
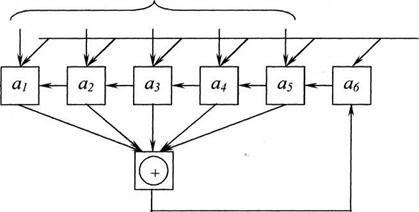
На основі (n, n- 1) - кодів з dmin = 2 або кодів Хеммінга з dmin = 3 і dmin = 4 можна побудувати коди з більш високими корректирующими властивостями. Для цієї мети, поряд із захистом кожної переданої комбінації описаним вище способом, здійснюють завадостійке кодування однойменних розрядів груп переданих комбінацій. Процес кодування можна пояснити за допомогою рис. 5.6.
Комбінації простого коду, що підлягають передачі по системі зв'язку, записуються у вигляді таблиці - кожна комбінація складає окремий рядок цієї таблиці (інформаційні символи). Потім здійснюється кодування по рядках і стовпцях. У загальному випадку для кодування рядків і кодування стовпців можна використовувати різні коди. Надлишкові елементи дописують до кожного рядка (перевірка по рядках) і до кожному колонку (перевірка по стовпцях). Перевірка перевірок здійснюється кодуванням стовпців, складених з надлишкових елементів рядків або кодуванням рядків, складених з перевірок стовпців. Наступне введення надмірності здійснюється для захисту блоків інформації, представлених на рис. 5.6. Процес кодування пояснюється на рис. 5.7. З блоків інформації, захищених двома перевірками, складається паралелепіпед. Надлишкові розряди третьої перевірки утворюють паралелепіпед, виділений потовщеною лінією.
5 ел. комбінація
В результаті итеративного кодування виходять групові коди, які мають наступну важливу властивість.
Теорема 5.3. Мінімальна кодова відстань ітеративного коду дорівнює добутку мінімальних кодових відстаней, кодів, його складових.
Дійсно, якщо в разі двох перевірок мінімальна вага одного коду дорівнює, а іншого, то вектор ітеративного коду має, принаймні, одиниць в кожному рядку і елементів в кожному стовпці і, отже, не менше одиниць.
Аналогічні міркування можна продовжити і на випадок більшого числа перевірок.
Породжує матриця ітеративного коду може бути побудована наступним чином.
Нехай GA - породжує матриця коду, використовуваного для перевірки по рядках, а GВ - породжує матриця коду, використовуваного для перевірки по стовпцях, тоді породжує матриця ітеративного коду (GAВ) має вигляд:
Запис означає, що на місцях "1" в матриці GA записується матриця GВ. а замість "0" записується матриця з одних нулів, розміри якої дорівнюють розмірам GВ. Так, наприклад, якщо для перевірки по рядках і стовпцях використовується (6, 5) - код з перевіркою на парність, то