координатні простору

Увага! Даний сайт не оновлюється. Нова версія: shatalov.su

Перетворення координатних просторів. Перейти.
Спуск і перспективна проекція. Перейти.

Перш ніж приступати до висновку графіки на екран, необхідно розглянути яким чином графічні об'єкти представляються зсередини.

В DirectX використовується кілька координатних просторів.

Світове координатне простір (World space)

У світовому координатном просторі описуються всі графічні об'єкти. Саме в цьому просторі можна "побачити" весь віртуальний світ. Ще цей простір називають глобальним або універсальним.

Чому не можна обмежитися тільки одним простором - світовим? Справа в тому, що використання декількох просторів сильно спрощують життя.

У сонячній системі для зручності розрахунку орбіт планет використовується геліоцентрична система координат (центр - Сонце). Але траєкторію руху Місяця навколо Землі набагато простіше уявити не в геліоцентричної, а в геоцентричної (центр - Земля) системі координат. Тут ми бачимо приклад використання двох систем координат - світовий і об'єктної. Те ж саме і в комп'ютерних іграх.

Тут варто пам'ятати, що місце розташування - воно відносно. Місце розташування об'єкта можна описати в різних координатних просторах: траєкторію Місяця можна показати і в геоцентричної і в геліоцентричної системи, але в першій це зробити простіше.

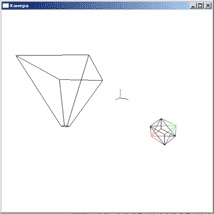
Розглянемо картинку, на якій зображено світове координатне простір. У просторі розташований один об'єкт - трикутник, і камера, яка спрямована в бік трикутника. І у камери і у трикутника свої координатні простору.

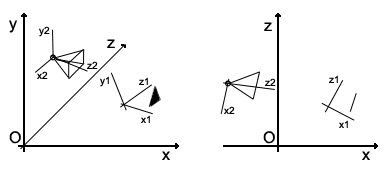
На другій картинці ця ж сцена, тільки вид зверху. Тут трикутник представлений у вигляді рисочки. Усі наступні картинки будуть використовувати або вид збоку (осі x, y) або вид зверху (осі x, z).

Об'єктне координатне простір (object space)

Саме в об'єктному координатном просторі відбувається побудова моделі (об'єкта).

Початок об'єктного простір потрібно розташовувати так, щоб було зручніше створювати об'єкт. Іноді початок об'єктного простору збігається з центром мас моделі.

На зображенні можна бачити простір трикутника описується осями x1, y1.

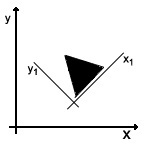
Якщо об'єкт складний, то вводяться додаткові простору - для спрощення анімації. Але нам до цього ще далеко.

Інерційний координатне простір (inertial space)

Ми введемо ще одне додаткове координатне простір - інерційний. Воно не використовується в реальності, але дозволяє спростити сприйняття того, як взаємодіють координатні простору. Подивимося на картинку:

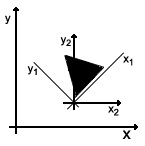
Тут представлені: об'єктне (x1, y1) і інерційний (x2, y2) простору.

Напрямок осей інерційного простору збігається з напрямком осей світового простору, а початок координат інерційного простору збігається з початком координат об'єктного простору.

Щоб "потрапити" з об'єктного простору в інерційного, потрібно обертання. А з інерційного простору дуже легко потрапити в світове. Для цього використовується переміщення. Інерційний простір дозволяє відокремити ці дві операції (обертання і переміщення).

Координатне простір камери

Камера - це уявлення користувача у віртуальному світі. Саме через камеру гравець бачить маленьку частину світового простору.

У камери є напрям - в який бік дивиться користувач і поля (сектора) огляду: по вертикалі і по горизонталі.

Напрямок камери (погляд гравця) завжди збігається з позитивним напрямком осі z в координатному просторі камери.

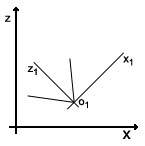
Визначення координатних просторів

Ми з'ясували які простору існують в DirectX: світове, об'єктне (у кожного об'єкта своє) і простір камери. Тепер потрібно з'ясувати яким чином ці простору взаємодіють.

У кожного простору є осі і початок координат - точка перетину осей (позначається як точка О). Початок координат - це місце розташування координатного простору. Наприклад: початок координат простору камери - це місце розташування (координати) цього простору в світовому просторі. Осі задають орієнтацію простору.

Перетворення координатних просторів

Знаючи координати об'єктного простору, можна будь-яку точку цього об'єкта висловити в світових координатах, і навпаки, будь-яку точку світових координат можна виразити в координатах об'єктного простору.

Розберемо ситуацію, коли об'єктні координати збігаються з інерційними. Припустимо у нас є трикутник в об'єктному просторі з координатами (0,0) (1,1) (1,0). Координати цього простору в світі - (23, 12). Щоб перетворити точки трикутника в світові координати досить координати кожної точки скласти з координатами об'єктного простору: (23,12) (24,13) (24,12) - ось так виглядає трикутник в світових координатах. Просто, правда?

Щоб перетворити координати якоїсь точки зі світових в об'єктні, потрібно з координат цієї точки відняти координати об'єктного простору.

Якщо об'єктні координати не збігаються з інерційними, то спочатку потрібно провести обертання, все інше без ізененій.

Важливе зауваження: при перетвореннях координатних просторів, координати об'єктів не переміщаються. Ми просто висловлюємо розташування об'єктів в різних координатних просторах.

Арканоід

Камера

клітини

спрайт