При роботі з тривимірною графікою використовується кілька видів систем координат. Для відображення двовимірних об'єктів нам була потрібна відповідна система координат з двома осями - горизонтальною віссю X і вертикальною віссю Y. Нагадаємо, що екранна система координат для двовимірної графіки має початок (точку 0,0) в лівому верхньому кутку монітора, позитивна частина осі X розташовується праворуч від початку координат, позитивна частина осі Y - знизу.
Для роботи з тривимірними об'єктами нам знадобиться ще одна вісь - вона називається вісь Z. Існує кілька варіантів тривимірних систем координат, зокрема, поширені так звані правобічна і лівостороння системи. Ми будемо користуватися правобічної системою - вона застосовується в XNA Framework. Її схематичне зображення наведено на рис. 1.
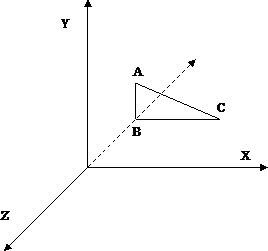
Мал. 1. Правосторонняя система координат
Особливість цієї системи координат полягає в тому, що початок координат можна зіставити з лівим нижнім кутом монітора, позитивна частина осі X знаходиться праворуч від початку координат, позитивна частина осі Y - зверху, а позитивна частина осі Z - спереду. А це означає, що видима частина осі Z - це її негативна частина. Ця частина осі перебуває ніби «в глибині монітора», в той час, як позитивна частина знаходиться «попереду монітора». На рис. 1. пунктиром зображена негативна частина осі Z.
У двовимірної системі координат існує поняття точки - її координати задаються двома значеннями - X і Y. Точки існують і в тривимірній системі координат - вони задаються вже трьома значеннями - X, Y, Z.
Точки використовують для того, щоб ставити координати вершин багатокутників (полігонів), зокрема - трикутників. Так, трикутник, зображений на рис. 1. заданий трьома крапками - A, B, C.
Як правило, більш складні тривимірні об'єкти будуються саме з трикутників.
У тривимірній графіці існує таке поняття, як грань (face). Це - плоский об'єкт, який визначають кілька вершин. У нашому випадку звичайний трикутник - це саме грань. З кількох плоских граней можна зібрати об'ємний об'єкт.
Чим більше трикутників використано при побудові моделі - тим більше деталізованої вона виходить. Точки, що відповідають вершинам трикутника, який можна зобразити у тривимірному просторі, називаються вершинами. Можливо, вам зустрінеться множину слова вершина: «вершини» виглядає по-англійськи як «vertices». Іноді для позначення вершин використовують кальку з англійської - вертекс.
Трикутник не випадково була обрана в якості базової геометричної фігури - по-перше - цей багатокутник завжди є опуклим, по-друге - неможливо розташувати три точки таким чином, щоб вони не належали одній площині. Тобто, трикутник - це фігура, яка завжди є опуклою і плоскою, що дозволяє з успіхом використовувати його в цілях тривимірної графіки.
Кілька граней, з яких складається тривимірний об'єкт, називаються сіткою (mesh). "Сітка" являє собою набір трикутників.
Ще одне поняття, яке стане в нагоді вам при роботі з тривимірною графікою - це поняття вектора. Вектор (vector), так само як і точка, може бути визначений трьома параметрами, однак він описує не положення в просторі, а напрямок і швидкість руху.
Вектор має початок і кінець, для його повного визначення потрібно знати координати точки початку і кінця вектора, тобто, замість трьох значень координат нам знадобиться вже шість значень. Однак, якщо за замовчуванням прийняти за початок вектора початок координат (точку 0,0,0) - тоді для його визначення вистачить і трьох точок.
Наприклад, вектор з координатами (1,0,0) означає: «напрямок - вправо, швидкість - 1». Якщо відкласти цей вектор від початку координат, то добре видно, що він спрямований саме вправо (рис. 2.).
Напрямок вектора визначається положенням другої точки щодо першої (в нашому випадку - положення точки кінця вектора, якої задається вектор щодо початку координат), а швидкість - довжиною вектора - тобто - різницею між початковою і кінцевою точкою. У нашому випадку довжина вектора збігається з координатами його кінця.
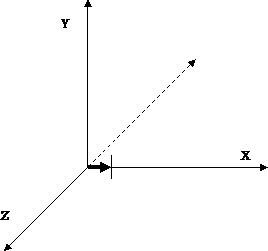
Мал. 2. Вектор (1,0,0)
Існує особливий вид векторів - нормалі (normals). Нормалі можуть бути побудовані для граней і для вершин об'єкта. Нормалі для граней перпендикулярні цим гранях. Вони використовуються при розрахунку кольору об'єкта.
Перетворення в тривимірному просторі
Знаючи координати вершин полігонів, з яких складається об'єкт, ми можемо розташувати його в просторі. Тепер потрібно розібратися зі зміною положення об'єктів в просторі. Існує кілька основних операцій, які можуть використовуватися для переміщення об'єктів в тривимірному просторі. Це - переміщення (translation), обертання (rotation) і масштабування (scale).
Результати роботи графічної підсистеми тривимірної гри ми бачимо на плоскому екрані монітора - змодельована комп'ютером тривимірна сцена проектується на двовимірну поверхню. При проектуванні потрібно вибрати точку, яка виконує роль камери, що дозволяє бачити тривимірний простір. У свою чергу, об'єкти в тривимірному просторі можуть переміщатися відповідно до певних правил. Для управління всім цим використовуються кілька матриць. Це - світова матриця (World Matrix), матриця виду (View Matrix) і матриця проекції (Projection Matrix).
Матрицю можна представити у вигляді таблиці, що складається з m рядків і n стовпців. У комп'ютерній графіці застосовуються матриці 4х4. Перших три стовпці цієї матриці відповідають за модифікацію координат X, Y, Z вершин об'єкта, який бере участь в трансформації.
Світова матриця дозволяє задавати перетворення - переміщення, обертання і трансформації об'єктів.
Матриця виду дозволяє управляти камерою.
Матриця проекції служить для настройки проекції тривимірної сцени на екран.
Припустимо, є трикутник, заданий наступними вершинами (табл. 1.).
Таблиця 1. Вершини трикутника до переміщення
При переміщенні цього трикутника на 10 позицій по осі X ми повинні додати по 10 до кожної з координат X його вершин. В результаті вийде матриця такого виду (табл. 2.).
Таблиця 2. Вершини трикутника після переміщення
Того ж ефекту можна досягти, помноживши координати кожної з вершин на світову матрицю. Для цього координати вершини представляють у вигляді матриці, що складається з одного рядка і чотирьох стовпців. У перших трьох стовпці містять координати X, Y, Z, в четвертому - 1. Світова матриця представлена у вигляді таблиці 4х4. Ось як виглядає операція множення матриць (формула 1.):
Формула 1. Множення матриці вершини і світової матриці
При перетворенні кожна з вершин множиться на світову матрицю.
Кожне з перетворень в просторі вимагає особливої настройки світової матриці. У формулі 2. наведено шаблон світової матриці, яка дозволяє переміщати об'єкти в просторі.
Формула 2. Світова матриця для переміщення об'єкта
тут # 916; X, # 916; Y і # 916; Z - це збільшення координат X, Y і Z.
Світова матриця для обертання об'єктів навколо осі Х виглядає так (формула 3.).
Формула 3. Світова матриця для обертання по осі Х
тут # 945; - кут повороту в радіанах
Світова матриця для обертання об'єктів по осі Y виглядає так (формула 4.)
Формула 4. Світова матриця для обертання по осі Y
Матриця для обертання об'єктів навколо осі Z приведена у формулі 5.
Формула 5. Світова матриця для обертання по осі Z
Формула 6. представляє матрицю, яка служить для трансформації об'єктів.
# 966; x, # 966; y, # 966; z - це коефіцієнти масштабування, які застосовуються до вершин. Вони дозволяють «стискати» або «розтягувати» об'єкти.
Інші типи матриць:
Матриця проекції дозволяє управляти проектуванням сцени на екран.
Перший - це перспективна проекція (Perspective projection). У цій проекції об'єкти виглядають так само, як ми звикли їх бачити в реальному світі. Об'єкти, які розташовані далі, здаються менше об'єктів, розташованих ближче.
Другий вид проекції - це ортогональна проекція. Тут об'єкти проектуються на площину екрану без урахування перспективи.
Освітлення об'єктів в іграх виконує ту ж роль, яка відведена йому в реальному світі. Існує безліч типів освітлення.
Навколишній розсіяне світло (ambient light) - це світло, яке освітлює всі об'єкти сцени з однаковою інтенсивністю. Джерело розсіяного світла не має місця розташування.
Точкове джерело світла (point light) - це джерело, яке випромінює світло в усіх напрямках. Його можна порівняти зі світлом, що виходить від лампочки, не прикритої абажуром.
Направлене джерело світла (directional light). Це джерело, на відміну від точкового, не має місця розташування, проте має орієнтацію
Зональний джерело світла (spot light) або прожектор має місце розташування, орієнтацію, а його світловий потік обмежений у формі конуса.
Джерела світла можуть мати різну інтенсивність, різний колір, при висвітленні сцен можна використовувати кілька різних джерел. Все це робить освітлення найважливішим елементом тривимірної графіки.
Шейдери, або шейдерниє програми - це програми, які дозволяють застосовувати до моделей різні ефекти. Вони пишуться на спеціальній мові програмування, як правило, не вручну, а з використанням відповідного програмного забезпечення. Шейдери діляться на верхові і піксельні. Вершинні шейдери дозволяють застосовувати різні ефекти до вершин моделей, піксельні шейдери обробляють колір кожного з пікселів моделі перед виведенням її на екран.
Текстури - це растрові (двовимірні) зображення, які накладаються на тривимірні моделі. Наприклад, тривимірна модель автомобіля може являти собою автомобіль, який як би «вирізаний» з твердого матеріалу, а після накладення на цю модель відповідної текстури автомобіль набуває кольору, створюється ілюзія наявності у нього дрібних деталей оформлення і т.д. Мінімальна одиниця текстури називається тексель. Чим більше пікселів доводиться на один тексель, ніж большьше дозвіл текстури - тим більш якісною буде виглядати модель після накладення на неї текстури.