Метод перебору при вирішенні кубічних рівнянь отримав найширшу популярність.
Метод перебору при вирішенні кубічних рівнянь отримав найширшу популярність. Алгоритм його виконання зводиться до нижченаведеному.
Спочатку підберемо один з коренів рівняння використавши то властивість, що у кубічного рівняння незмінно присутня, принаймні, один дійсний корінь. причому цілий корінь кубічного рівняння з цілими коефіцієнтами буде дільником вільного членаd.
Коефіцієнти цих рівнянь. як правило, підібрані так, що необхідний корінь є невелике ціле число. таке як: 0, ± 1, ± 2, ± 3.
І, відповідно, потрібно виявити корінь серед цих чисел і перевірити його шляхом підстановки в рівняння.
Приймемо даний корінь за x 1.
На наступному етапі розділимо многочленax 3 + b x 2 + cx + d на двучленx - x 1.
Застосуємо теорему Безу (поділ многочлена на лінійний двочлен), згідно з якою цей поділ без залишку можливо, і за підсумком обчислень отримуємо многочлен другого ступеня. який дорівнює нулю. Вирішуючи отримане квадратне рівняння. ми знайдемо (чи ні!) два інших кореня.
Проаналізуємо хід рішення рівняння: x 3 - 3x 2 - 13x + 15 = 0.
Знайдемо перший корінь, підставляючи в рівняння цифри: 0, ± 1, ± 2, ± 3 отримуємо, що 1 є коренем. Далі розділимо ліву частину цього рівняння на двучленx- 1. і отримаємо:
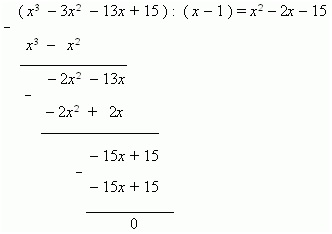
Далі, обчислимо корені квадратного рівняння. x 2 - 2x - 15 = 0.