Мал. 73. Побудова лінії ската в площині:
а - заданої следаміплоскості Р; б -в площині, заданої # 916; СDЕ
кут # 946; заданої площині - кут нахилу заданої площині до фронтальної площини проекцій V визначає лінія найбільшого нахилу-пряма, що лежить в заданій площині і перпендикулярна фронталі цій площині.
Побудова лінії найбільшого нахилу до фронтальної площини проекцій V виконується за схемою побудови лінії ската (рис. 74б):
а) в заданій площині (CDE) будують проекції фронталі D1 (d1; d '1');
б) проводять фронтальну проекцію лінії найбільшого нахилу перпендикулярно фронтальній проекції фронталі в будь-якому зручному або необхідному місці на кресленні. У нашому випадку лінія найбільшого нахилу проводиться з точки Е (а'е '⊥ d'1');
в) горизонтальна проекція лінії найбільшого нахилу будується за умовою приналежності її даній площині.
На рис. 74а наведено побудову лінії найбільшого нахилу до фронтальної площини проекцій V в площині Р. заданої слідами. Фронтальний слід площини РV є нульовою Фронтале цій площині. Фронтальна проекція шуканої лінії d'e 'проводиться під прямим кутом до РV в будь-якому зручному місці. Горизонтальна проекція de будується з умови приналежності прямий DE площині Р.
Для того щоб знайти кути # 945; або # 946; ліній найбільшого нахилу, можна використовувати спосіб прямокутного трикутника.
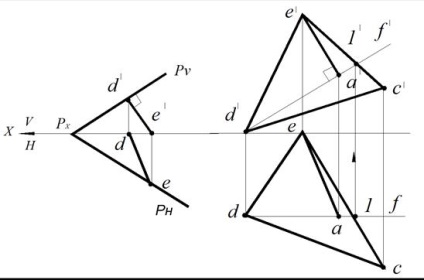
Мал. 74. Побудова лінії найбільшого нахилу до фронтальної площини проекцій:
а - в площині Р. заданої слідами; б -в площині, заданої # 916; СDЕ
3.5.2.1. Визначення кутів нахилу площини до площин проекцій
по лініях найбільшого нахилу
Лініями найбільшого нахилу площини до площин проекцій V і Н називаються прямі, що лежать в даній площині і перпендикулярні відповідно до фронталі або горизонталі цій площині.
Лінії найбільшого нахилу можна також проводити перпендикулярно слідах площині, т. К. Фронталь площини паралельна фронтальному сліду ( «нульовий» фронталі), горизонталь площини паралельна горизонтальному сліду ( «нульовий» горизонталі) (рис. 75).
AB - лінія найбільшого нахилу (ската) до площини Н.
AC - лінія найбільшого нахилу до площини V.
∠ # 945; - кут нахилу площини Р до площини проекцій Н = # 945; °.
∠ # 946; - кут нахилу площини Р до площини проекцій V = # 946; °.
Розглянемо на конкретних прикладах способи визначення кутів нахилу заданої площині до площин проекцій V і H.
Визначення кутів нахилу заданої площині до площин проекцій V і H
способом прямокутного трикутника
Завдання 1. Визначити кут нахилу площини Р (АDE) до площини проекцій Н.
Рішення. Порядок виконання графічної частини завдання (рис. 76):
1. У площині Р провести горизонталь Н (h ', h).
2. З вершини А. перпендикулярно горизонталі, побудувати відрізок АВ - лінію ската, що лежить в цій площині; побудова лінії ската починається з горизонтальної проекції за умови, що | ab | ⊥ h.
3. Визначити дійсну величину відрізка АВ методом прямокутного трикутника, одним катетом якого буде горизонтальна проекція цього відрізка | ab |.
4. Потрібним кутом # 945; є кут між гіпотенузою | ат b | трикутника (abao) і горизонтальною проекцією лінії ската ab.
Мал. 75. Просторова модель ліній найбільшого нахилу площини
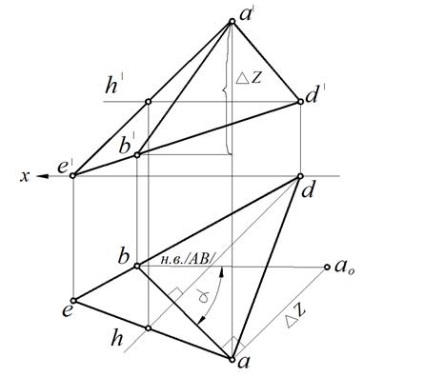
Мал. 76. Визначення ∠ # 945; площині # 8710; АЕD по лінії ската
Завдання 2. Визначити кут нахилу площини Р до площини проекцій V.
Рішення. Порядок виконання графічної частини завдання (рис. 77):
1. У площині Р провести фронталь F (f ', f).
2. З вершини А перпендикулярно фронталі, провести відрізок | АС | - лінію найбільшого нахилу, що лежить в цій площині, побудова лінії найбільшого нахилу починається з побудови фронтальної проекції за умови, що a'c '⊥ f'.
3. Визначити натуральну величину відрізка [АС] методом прямокутного трикутника, одним катетом якого є його фронтальна проекція.
4. Потрібним кутом # 946; є кут між гіпотенузою АОС 'трикутника a'c'ao і фронтальною проекцією a'c'.
Мал. 77. Визначення ∠ # 946; площині # 8710; EAD по лінії найбільшого нахилу
Завдання 3. Побудувати трикутник з вершиною в точці С і підставою, рівним висоті трикутника за величиною, що лежить на прямій (AD). Визначити кути нахилу площини трикутника до площин проекцій V і Н. А (10; 10; 15); З (30; 40; 30); D (60; 30; 15); (Рис. 78-80).
Дане завдання складається з декількох невеликих завдань
1. Побудова проекцій трикутника.
2. Визначення кутів нахилу площини трикутника до площин проекцій V і Н.
Порядок виконання графічної частини завдання:
1. Побудова проекцій трикутника.
1.1. За заданими координатами будуємо фронтальні і горизонтальні проекції точок А, С і D. Через точки А і D проводимо проекції прямої AD відповідно площин проекцій. Згідно вихідних даних (АD) є горизонтальною прямою рівня (рис. 78).
1.2. З огляду на те, що (AD) || Н. побудова проекцій висоти трикутника починаємо з горизонтальної проекції (на підставі теореми про прямому куті), проводимо [с) ⊥ (а d). Луч [c) при перетині з (аd) дає точку k. Фронтальна проекція висоти c'k 'вибудовується по проекційної залежності. Визначаємо довжину | CK |.
1.3. Методом прямокутного трикутника, за один катет приймаючи горизонтальну проекцію (сk) визначаємо довжину | CK |. Вона дорівнює гіпотенузі kco, | CK | = | Kco | = Н.в.
1.4. Будуємо горизонтальну проекцію підстави трикутника op = | CK | на проекції відрізка AD. відкладаючи його без спотворення і з огляду на, що підстава трикутника в точці К ділиться навпіл. Отримуємо точки про і р. Фронтальна проекція підстави трикутника вибудовується по проекційної залежності.
1.5. Будуємо проекції шуканого трикутника cop і с'о'р '.
2. Визначення кутів нахилу площини трикутника до площин проекцій V і Н.
2.1. Визначаємо кут нахилу площини # 916; РІС до площини проекцій Н.
Аналізуючи дані (рис. 78), відзначаємо, що висота # 916; РІС - відрізок СК - є лінією ската площині трикутника до площини проекцій Н. т. К. Ck ⊥ ad. а підстава ЗР || H. т. е. є горизонталлю площини трикутника. Отже, кут між cok і [ck] є кутом нахилу # 945; даної площини до площини проекцій Н.
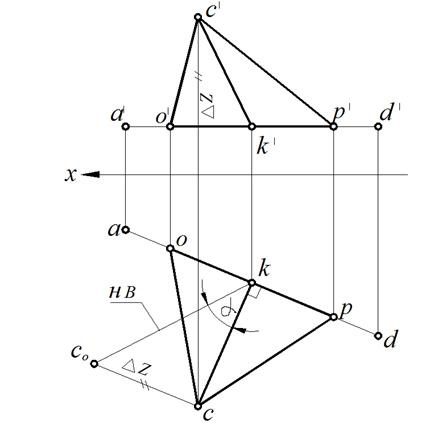
Мал. 78. Визначення ∠ # 945; площині # 8710; ОРС по лінії ската
2.2. Визначаємо кут нахилу площини # 916; РІС до площини проекцій V по лінії найбільшого нахилу.
Кут нахилу площини # 916; РІС до площини проекцій V визначається за допомогою лінії найбільшого нахилу MN. перпендикулярної до фронталі трикутника, [MN] ⊥ F.
Хід рішення (рис. 79):
2.2.1.Через вершину трикутника Р проводимо фронталь F.
Мал. 79. Визначення ∠ # 946; площині # 8710; ОРС по лінії найбільшого нахилу
2.2.2. У площині # 916; РІС будуємо пряму MN - лінію найбільшого нахилу, де фронтальна проекція m'n '⊥ f'. а горизонтальна проекція mn будується по проекційної залежності.
2.2.3. Визначаємо довжину відрізка [MN] методом прямокутного трикутника, побудованого на фронтальній проекції, m'n '- є його натуральної величиною.
2.2.4. У прямокутному трикутнику кут між m'n 'і n'mo є кутом найбільшого нахилу # 916; РІС до площини проекцій V. т. Е. ∠ # 946 ;.
Отже, повертаємося до умові завдання і на основі вищерозглянутого матеріалу вирішуємо цю задачу на одному кресленні.
Завдання 4. Побудувати трикутник з вершиною в точці С і підставою, рівним висоті трикутника і лежачим на прямий AD. Визначити кути нахилу площини трикутника до площин проекцій V і Н.
Рішення. Порядок виконання графічної частини завдання:
2. Будуємо проекції висоти трикутника, починаючи з фронтальним - c'k '⊥ a'd', горизонтальна проекція висоти вибудовується по проекційної приналежності.
3. Будуємо підставу трикутника OP. o'p '= c'k'. добудовуємо горизонтальну і фронтальну проекції шуканого # 916; СОР.
4. # 916; СОР ^ V = ∠ # 946 ;, СК - лінія найбільшого нахилу до площини V.
5. # 916; СОР ^ Н = ∠ # 945 ;, PE - лінія ската до площини Н.
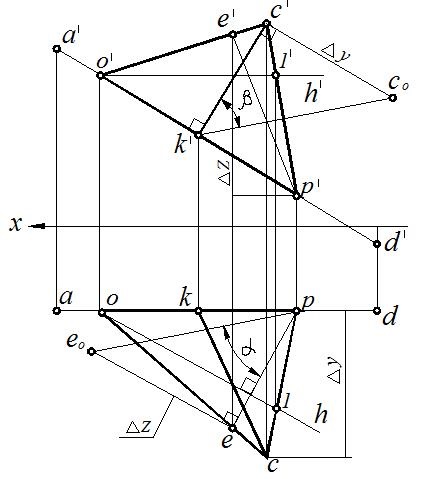
Мал. 80. Повне рішення задачі
Визначення кутів нахилу площини загального положення
до площин проекцій методом заміни площин проекцій
1. Визначення кута нахилу площини загального положення
до горизонтальної площини проекцій
Завдання. Дана площину кута # 945; заданої площині. Необходімопреобразовать комплексний креслення так, щоб площина # 916; ABC став фронтально проецирующей площиною в новій системі площин.
Порядок виконання графічної частини завдання:
2. Проводимо в площині # 916; ABC горизонталь DC.
3. Вісь проекції X1 - горизонтальний слід площини V1 - проводимо перпендикулярно прямий cd на будь-якій відстані від точки d.
4. Проводимо з точок a, b і d лінії зв'язку до нової осі X1.
На нову площину проекцій V1 площину # 916; ABC відобразилася в прямо лінію, т. Е.стала фронтально проецирующей площиною. На новій площині проекцій V1 кут нахилу площини # 916; ABC до горизонтальної площини проекцій # 945; відображений без спотворення (рис. 81).
Мал. 81. Визначення кута ∠ # 945; площині # 8710; АВС
2. Визначення кута нахилу площини загального положення до фронтальної площини проекцій методом заміни площин проекцій
Завдання. Дано: площину # 916; ABC - площину загального положення.
Для визначення кута # 946; заданої площині необхідно перетворити комплексний креслення так, щоб площина # 916; ABC став горизонтально проецирующей площиною в новій системі площин.
Порядок виконання графічної частини завдання:
2. Проводимо в площині # 916; ABC фронталь DC.
3. Вісь проекції X1 - фронтальний слід площини Н1, проводимо перпендикулярно прямий c'd 'на будь-якій відстані від точки з'.
4. Проводимо з точок а ', b', і d 'лінії зв'язку до нової осі X1.
На нову площину проекцій Н1 площину # 916; ABC відобразилася в пряму лінію, т. Е. Стала горизонтально проецирующей площиною. На новій площині проекцій Н1 кут нахилу площини трикутника АВС до фронтальної площини проекцій # 946; відображений без спотворення (рис. 82).
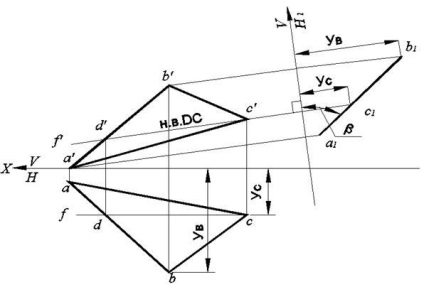
Мал. 82. Визначення ∠ # 946; площині # 8710; АВС