Лінією найбільшого ската називається пряма, перпендикулярна будь-горизонталі площини. Л.Н.С. застосовується для визначення кута нахилу площини до площини проекцій π1 - α (ріс.58, 59). АВ -лінія найбільшого ската. А'В'┴hoαα - кут нахилу АВ до π1. це кут між горизонтальною проекцією і натуральної величиною відрізка АВ.
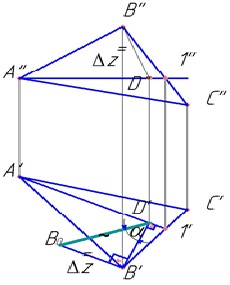
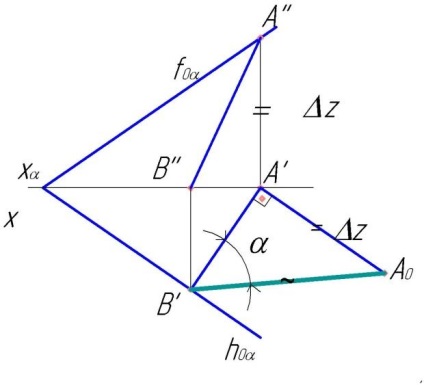
Визначаємо справжню величину відрізка АВ. На горизонтальній проекції будуємо прямокутний трикутник з катетами А'В 'і Δz. Кут α між істинною величиною і горизонтальною проекцією відрізка АВ є кут нахилу площини до горизонтальної площини проекцій.
На ріс.58 побудована Л.Н.С. BD.
У Δ АВС провели горизонталь А1 і з будь-якої точки площини (в прикладі (∙) В провели Л.Н.С. BD (B'D '┴A'1'). Кут α - це кут нахилу трикутника АВС до горизонтальної площини проекцій .
Побудова лінії перетину двох площин
Дві площини завжди перетинаються по прямій. Для побудови лінії перетину досить знайти дві точки цієї лінії або одну точку і напрямок цієї прямої. Розглянемо кілька випадків перетину площин.
Приклад 1. Дві площини α і γ перетинаються по прямій MN (ріс.60) в межах креслення.
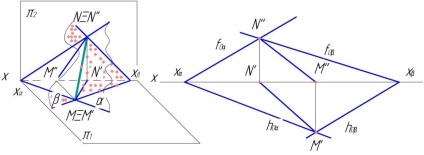
Приклад 2. Перетин двох площин відбувається по горизонталі (або фронталі).
На ріс.61, 62 фронтальна проекція лінії перетину збігається зі слідом f0γ. а горизонтальна легко знаходиться як горизонтальна проекція горизонталі в цій площині.
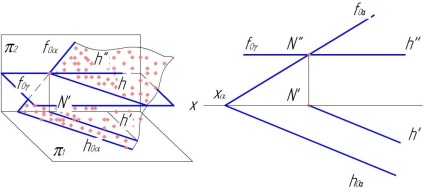
Приклад 3. У межах креслення перетинаються тільки два горизонтальних сліду заданих площин α і β (ріс63).
Крапку М знаходимо в перетині горизонтальних слідів. Для знаходження точки N візьмемо додаткову допоміжну горизонтальну площину γ. Ця січна площина буде перетинати площині α і β по горизонталях. Горизонтальні проекції цих горизонталей в перетині дадуть другу точку лінії перетину площин α і β - точку N (ріс.64).
Приклад 4. Одна площину задана слідами загального положення, друга площина задана двома пересічними прямими загального положення (ріс.65).
1. Проведемо допоміжну площину приватного положення, наприклад, площина горизонтального рівня β || π1 (fоβ || х) (рис. 66).
2. Площина β перетне площину α по горизонталі h.h ''

3. Площина β перетне площину (а∩b) по прямій (2-3).
4. Прямі h і 2-3 перетинаються в точці M (M 'і M' '). де M '= h'∩ (2'-3'), а M ''

5. Для побудови другої загальної точки проведемо ще одну допоміжну площину γ || π1 (fоγ || х) (ріс.67).
6. Площина γ перетне площину α по горизонталі h1: h1 ''

7. Площина γ перетне площину (а∩b) по прямій (5-6).
8. Прямі h1 і 5-6 перетнуться в точці М (М '' і М '). де М '= (5'-6') ∩h1 ', М' '

9. З'єднаємо однойменні проекції точок М і N і отримаємо проекції лінії перетину (М'N ') і (М''N' ').
Приклад 5. Площина ΔАВС приватного положення (ΔАВС
оскільки ΔАВС
1. Відзначимо загальної горизонтальної проекції Q 'і T' на перетині горизонтальних проекцій трикутників АВС і MNK (ріс.69).
2. Фронтальні проекції Q '' і T '' шукаємо на лініях проекційної зв'язку в ΔM''N''K ''.
3. Лінія перетину QT визначена QT (Q''T '' і Q'T ').
4. Визначимо видимість плоских фігур, тому що площині вважаються непрозорими. Видимість горизонтальної проекції фігур визначати не треба, тому що ΔАВС проектується в пряму лінію, проекція M'N'K 'видима. Визначимо видимість плоских фігур відносно площини проекцій π2. Для цього розглянемо конкуруючі точки 1 і 2. лежать на перехресних прямих ВС і МK. Фронтальні проекції 1 "і 2" збігаються, а горизонтальна проекція 2 'знаходиться перед горизонтальною проекцією 1'. Точка 1 '' невидима щодо площини проекцій π2. Далі розмірковуємо так: точка 2 лежить на ΔАВС. отже, фронтальна проекція ΔА''В''С '' видима на π2 з того боку, де знаходяться точки 1 '' і 2 ''. Після фронтальної проекції лінії перетину Q "і T" видимість ΔА''В''С '' змінюється на протилежну, тобто він стає невидимим (ріс.69).