Геометрична інтерпретація методу хорд полягає в наступному
(Ріс.6.2.3-8).
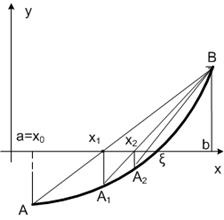
Проведемо відрізок прямої через точки A і B. Чергове наближення x1 є абсцисою точки перетину хорди з віссю 0х. Побудуємо рівняння відрізка прямої:
Покладемо y = 0 і знайдемо значення х = х1 (чергове наближення):
Повторимо процес обчислень для отримання чергового наближення до кореня - х2:
У нашому випадку (ріс.6.2.11) і розрахункова формула методу хорд матиме вигляд
Ця формула справедлива, коли за нерухому точку приймається точка b, а в якості початкового наближення виступає точка a.
Розглянемо інший випадок (рис. 6.2.3-9), коли.
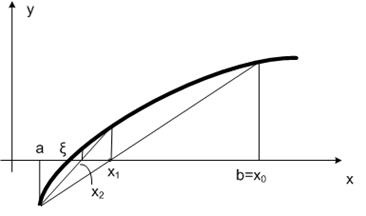
Рівняння прямої для цього випадку має вигляд
Чергове наближення х1 при y = 0
Тоді рекуррентная формула методу хорд для цього випадку має вигляд
Слід зазначити, що за нерухому точку в методі хорд вибирають той кінець відрізка [a; b], для якого виконується умова f (x) # 8729; f ¢¢ (x)> 0.
Таким чином, якщо за нерухому точку взяли точку а, то в якості початкового наближення виступає х0 = b, і навпаки.
Достатні умови, які забезпечують обчислення кореня рівняння f (x) = 0 за формулою хорд, будуть тими ж, що і для методу дотичних (метод Ньютона), тільки замість початкового наближення вибирається нерухома точка. Метод хорд є модифікацією методу Ньютона. Різниця полягає в тому, що в якості чергового наближення в методі Ньютона виступає точка перетину дотичної з віссю 0Х, а в методі хорд - точка перетину хорди з віссю 0Х - наближення сходяться до кореню з різних сторін.
Оцінка похибки методу хорд визначається виразом
Умова закінчення процесу ітерацій за методом хорд
У разі, якщо M1 <2m1. то для оценки погрешности метода может быть использована формула | xn - xn-1 | £ e.
Приклад 6.2.3-4. Уточнити корінь рівняння e x - 3x = 0, відокремлений на відрізку [0; 1] з точністю 10 -4.
Перевіримо умову збіжності:
Отже, за нерухому точку слід вибрати а = 0, а в якості початкового наближення прийняти х0 = 1, оскільки f (0) = 1> 0 і f (0) * f "(0)> 0.
Результати розрахунку, отримані з використанням формули
6.2.3-14, представлені в таблиці 6.2.3-4.
Необхідна точність досягається на 8-й ітерації. Отже, за наближене значення кореня можна прийняти х = 0.6191.
Схема алгоритму методу хорд приведена на рис. 6.2.3-10.
Вибір нерухомої точки, яка визначає вид розрахункової формули, проводиться шляхом порівняння одного з кінців відрізка [a; b] з початковим наближенням (x0 = a). Як нерухомого кінця відрізка (точка с) вибирається той, який не збігається з початковим наближенням.
Мал. 6.2.3-10. Схема алгоритму методу хорд