Тут і - прогин і кут повороту на початку системи координат, початок координат завжди розташовується в лівому крайньому перетині балки;
Z - відстань від початку координат до перетину, де визначається прогин і кут повороту;
а, в, с, d - відстань від початку координат до місця докладання відповідних зовнішніх сил m, p, q.
МЕТОДОМ Мора - ВЕРЕЩАГІНА
Для цього будуються епюри згинальних моментів від заданої зовнішньої навантаження (рис. 43, а), від одиничної сили (рис. 43б) при визначенні прогину і одиничного моменту - (рис. 43в) при обчисленні кута повороту, і проводиться "перемноження" відповідних епюр , тобто з одного епюри беремо її площа. а з іншого - ординату. розташовану під центром ваги взятої площі.
Основні правила множення епюр:
- результат позитивний, якщо епюри розташовані по одну сторін від осі балки, якщо по різні боки - результат негативний;
- позитивний результат перемноження епюр свідчить про те, що напрямок переміщення (лінійного і кутового) збігається з напрямком одиничних сил, при негативному результаті - протилежні напрямку одиничних сил;
- якщо обидві епюри (і) лінійні, то не має принципового значення з якою епюри брати площу. з якою ординату;
- якщо одна з епюр криволинейна (це), то площа обов'язково береться з неї;
- якщо складно обчислювати площу епюри, визначити координати центра ваги її і ординату. то при перемножуванні епюр і використовується прийом Симсона (формула 28) (рис. 44).
А, В, С - ординати з вантажною епюри
а, b, с - теж з одиничною епюри
- спина i-го ділянки балки
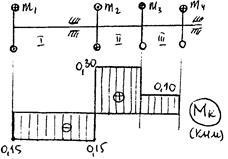
1. Визначаємо величину зовнішніх моментів, що скручують, перед кожним шківом (через потужність і обороти вала)
де N - потужність, КВт; n - число оборотів в хвилину.
2. Будуємо епюру крутних моментів, розбивши вал на ділянки I, II, III, застосовуючи метод розтину і прийнявши таке правило знаків для крутного моменту
якщо дивитися на залишену частину валу з боку перетину, то
На епюрі видно, що в перетинах, де прикладені зовнішні моменти виходять скачки, рівні за величиною цих моментів. Максимальна величина
3. Визначаємо діаметр вала за умовами міцності і жорсткості, застосовуючи формули (20), попередньо визначивши допустиме дотичне напруження
тут переведений в
З отриманих значень приймаємо діаметр валу d = 35 мм, забезпечуючи тим самим вимоги і жорсткості і міцності.
ЗАВДАННЯ № 33. Для заданого ступеневої кронштейна, навантаженого зовнішніми окручівающімі моментами m1 = 10 кНм і m2 = 30 кНм і защемленного з обох кінців, потрібно побудувати епюру крутних моментів Мк і при дозволяється дотичному напруженні [] = 80. Визначити діаметри суцільний і кільцевої частин (рис. 46). В кільцевої частини D = 2d, d0 = 0,8d, т. Е. C = = 0,4
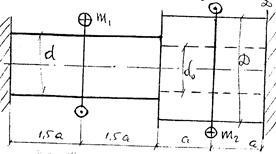
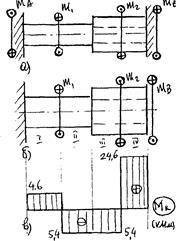
Перетворимо її в статично визначену, відкинувши наприклад опору "В", замінивши її дію опорним моментом "m". Відкинувши опору "В", ми дали можливість перетину В повертатися під дією всіх зовнішніх моментів, але ж в заданій системі перетин В жорстко защемлено, повороту не має. Відобразимо цей факт, склавши рівняння переміщень:
Використовуючи закон Гука при крученні запишемо
Скоротивши на "a" і жорсткість "", отримаємо
Тут і - полярні моменти інерції суцільної і кільцевої частин кронштейна. Їх співвідношення дорівнює
Вирішивши рівняння (31), отримаємо значення опорного моменту
Тоді з рівняння рівноваги визначаємо величину опорного моменту
Отримані позитивні значення опорних моментів і говорить про те, що їх напрямок було обрано вірно.
2. Розбиваємо задану систему на ділянки I, II, III, IV (рис. 47б). Межами ділянок є перетину, де прикладені зовнішні моменти і змінюється перетин. Будуємо епюри крутних моментів (рис. 47в) застосовуючи метод перетинів
3. З умови міцності при крученні визначаємо діаметри суцільний і кільцевої частин кронштейна, попередньо визначивши, як діють найбільші дотичні напруження
Таким чином, найбільші дотичні напруження діють в значеннях 2 ділянки, їх і порівнюємо з допускаються
Звідси діаметр суцільний частини d дорівнює
Тоді розміри кільцевої частини кронштейна складуть.
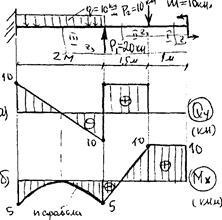
1. Введемо побудова епюр і М по ділянках справа, з боку вільного кінця (рис 48а і б)
Визначимо координату перетину, де поперечна сила проходить через нуль, в цьому перерізі згинальний момент має екстремальне значення
2. З умови міцності на прямому згині визначаємо розміри (номер швелера) перетину балки.
ПО сортаменту на швелера Гост 8240 - 82 [1] і враховуючи, що перетин складається з швелерів, приймаємо швелер № 10, якого.
Для заданно шарнірно опертої балки побудувати епюри поперечних сил і згинальних моментів і визначимо з яким запасом міцності вона буде працювати (рис. 49), якщо b = 60мм, h = 140мм, а = 35мм.
1. Визначаємо спочатку опорні реакції з умови рівноваги балки
Отже реакції визначені вірно.
2. Розбиваємо балку на ділянки I, II, III, IV, межами ділянок є перетину, де прикладені зовнішні сили. За допомогою методу перетину будуємо епюри і (рис. 49а і б)
третя ділянка (розглядаємо праву частину);
3. За епюрі бачимо, що найбільший згинальний момент дорівнює 20 кНм.
4. Обчислюємо величину максимальних нормальних напружень, що діють в балці, за формулою (22), попередньо визначивши осьової момент опору заданого перетину через осьовий момент інерції
5. Запас міцності балки визначаємо з умови міцності
; . що цілком достатньо.
Для заданої двотаврової балки (рис. 50) побудувати епюри і. підібрати переріз при = 160 МПа і перевірити його на міцність по дотичним напруженням, а так само визначити прогин в точці "C" і кут повороту перетину "K" двома способами: методом початкових параметрів і методом Море - Верещагіна.
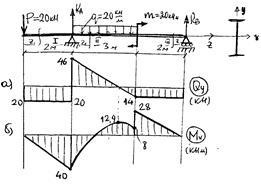
2. Будуємо епюри і. по ділянках (рис 50а і б)
координата перетину, де
3. Підбираємо двотавровий перетин балки з умови міцності за нормальними напруженням. звідси.
По сортаменту ГОСТ 8239 - 89 приймаємо двотавр № 22а, у якого. . .
4. Застосовуємо вибраного перетин на міцність по дотичним напруженням, застосовуючи формулу Д.І. Жуковського.
Допустиме дотичне напруження звичайно дорівнює
Отже, міцність по дотичним напруженням цілком забезпечена, бо
5. Визначаємо прогин "" в, т "C" і кут повороту перетину "K" (в нашому прикладі вони збігаються) методом початкових параметрів. Для цього поміщаємо початок координат в ліве крайнє перетин і записуємо
У цьому рівнянні обидва початкових параметра і невідомі. Для їх визначення складаємо рівняння прогинів для перетинів над опорами А і В, де ясно, що вони рівні 0.
Підставивши значення координат і зовнішніх сил, отримаємо два рівняння
Вирішивши їх, отримаємо
Тоді прогин перерізу "C" буде дорівнює
Кут повороту цього ж перетину
6. Визначаємо прогин перерізу "C" і кут повороту перетину "K" методом Мора - Верещагіна, для цього додатково до епюрі згинальних моментів від заданого навантаження (рис. 51а) будуємо епюри і від одиничних сил (51 б і в) і виробляємо перемноження відповідних епюр. В результаті отримаємо (див. Вираз 28) прогин
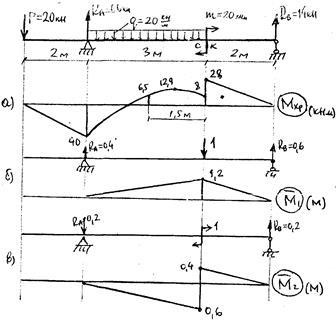
т. е. практично отримали однакову з методом початкових параметрів значення прогину.
теж практично збіглося зі значенням, отриманим за методом початкових параметрів.
Позитивне значення результатів перемноження епюр свідчить, що лінійні і кутові переміщення перетинів "C" і "K" збігаються з напрямками одиничних сил (прогин вниз, а поворот за годинниковою стрілкою).
ВАРІАНТИ ДОМАШНІХ ЗАВДАНЬ
У домашнє завдання № 3 входить вирішення 2 завдань на кручення і одного завдання на прямий вигин. Номер завдань, розрахункові схеми і вихідні дані відповідно до свого варіантом приймаються за таблицями № 3 (1 - а завдання), № 4 (2 - а завдання) і № 5 (3 - а завдання).
При виконанні домашньої роботи потрібно!
- побудувати епюру крутних моментів;
- визначити діаметри круглого суцільного або кільцевого перетину з умов міцності і жорсткості або максимальне дотичне напруження і запас міцності "K";
В 2 - ій задачі:
- розкрити статичної невизначеності заданої системи, скласти необхідне число рівнянь переміщень;
- побудувати епюру крутних моментів;
- з умов міцності визначити необхідні діаметри заданого перетину стрижня.
- побудувати епюри поперечних сил і згинальних моментів М для зазначеної балки;
- підібрати з умов міцності розміри поперечного перерізу заданої форми;
- визначити прогин в перерізі "C" і кут повороту перетину "K" методом початкових параметрів і методом Мора - Верещагіна.