Лекція 2.1. Визначення переміщень при вигині методом початкових параметрів. Визначення переміщень в балках змінного перерізу
Визначення переміщень при вигині методом початкових параметрів
Визначення переміщень методом безпосереднього інтегрування диференціального рівняння пружної лінії в разі балок з великою кількістю ділянок пов'язане зі значними труднощами у визначенні великої кількості постійних інтегрування.
Для зменшення великої обчислювальної роботи в даний час розроблений ряд методик. До них відноситься і метод початкового інтегрування.
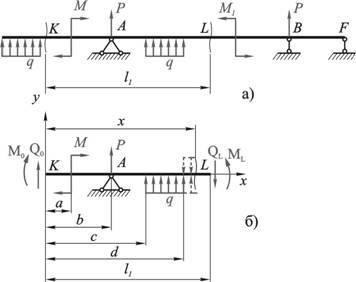
Розглянемо деяку частину балки довжиною (рис. 2.1.1, а), провівши перетину в точках і. На рис. 2.1.1, б зображений цей відрізок, навантажений наступними найбільш часто зустрічаються навантаженнями:
а) зосередженим моментом М в перетині з абсцисою;
б) зосередженої силою в перерізі з абсцисою;
в) рівномірно розподіленим навантаженням від перетину з абсцисою до перетину з абсцисою.
г) крім того, по кінцях розглянутої частини балки прикладені поперечні сили і згинальних моментів, які замінять дію подумки відкинутих частин балки.
Початок координат вибираємо в крайній лівій точці розглянутої балки і робимо його загальним для всіх ділянок балки.
Візьмемо довільне перетин на відстані від початку координат.
При виведенні рівнянь направлення всіх навантажень обрані так, щоб вони викликали позитивні згинальні моменти.
Вирази для згинальних моментів будемо складати, розглядаючи навантаження зліва від перетину з координатою. При включенні в рівняння зовнішнього зосередженого моменту помножимо його на множник. дорівнює одиниці. У разі обриву розподіленого навантаження її продовжують до кінця розглянутого перетину, а для відновлення дійсних вантажних умов вводять «компенсуючу» навантаження ».
Інтегрування будемо виробляти, не розкриваючи дужок.
Складаємо вираз згинального моменту для перетину з координатою
Складемо диференціальне рівняння пружної лінії
Інтегруємо обидві частини рівності, не розкриваючи дужок
Очевидно, що для
Отже, константи інтегрування і при підстановці початкових умов дорівнюватимуть куту повороту і прогину на початку координат. Прогин і кут повороту є початковими параметрами.
Для випадку декількох моментів і сил, а також кількох ділянок розподіленого навантаження рівняння записують у наступній формі:
Дане рівняння зазвичай називають універсальним рівнянням пружної лінії.
Диференціюючи універсальне рівняння прогинів, отримуємо рівняння кутів повороту перерізів
В універсальні рівняння підставляються тільки ті навантаження, які розташовані зліва від розглянутого перерізу. Початком координат приймається крайнє ліве перетин балки.
Таким чином, визначення переміщень по методу початкових параметрів зводиться в першу чергу до визначення величин початкових параметрів і. які визначаються з умов закріплення балки.
Визначимо прогин і кут повороту перетину вільного кінця консольної балки, навантаженої розподіленим навантаженням (Рис. 2.1.2).
У затисканні при заданому навантаженні буде виникати реакція і реакційний момент.
Очевидно, що при даному виді закріплення
Підставляємо навантаження в універсальні рівняння.