Теорія графів - це область математики, особливістю якої є геометричний підхід до вивчення об'єктів. Теорія графів та алгоритми на графах знаходять широке застосування в програмуванні. Поняття графа і поняття відносини - це равнооб'ёмние поняття. Теорія графів надає дуже зручний мову для опису програмних моделей. Картинки дозволяють відразу «побачити» суть справи на інтуїтивному рівні, доповнюючи і прикрашаючи виснажливі раціональні текстові докази і складні формули. Перші завдання теорії графів були пов'язані з вирішенням математичних розважальних завдань і головоломок.
Перша робота з теорії графів належить Л Ейлера (1736год), хоча термін «граф» вперше ввів в 1936 році угорський математик Денеш Кеніг.
Графом G (V, X) називається пара двох кінцевих множин: безліч точок і безліч ліній, що з'єднують деякі пари точок.
Точки називаються вершинами, або вузлами графа, лінії -ребрамі.
Нехай дано граф G (V, Х), де V = 1. V2 ...>-безліч його вершин, а Х (V1. V2) -його ребра.
Якщо елементи з Х розглядати як невпорядковані пари, то граф називається неорієнтованим. а пари називаються ребрами. Якщо ж елементи з E розглядати як впорядковані, то граф орієнтований. а пари - дуги.
Якщо ребро графа G з'єднує дві його вершини, то говорять, що це ребро їм інцидентне.
Дві вершини графа називаються суміжними, якщо існує інцидентне їм ребро.
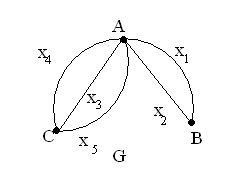
-суміжні вершини - А і В, А і С.
- вершин А і С інцидентне ребро х3
Якщо граф має ребро, у якого початок і кінець збігаються, то це ребро називається петлею.
Граф G (V, E) може мати ребра з однаковими парами виду Х (V, W).
Такі ребра називаються кратними, або паралельними.
На рис кратні ребра х1 (А, В) і х2 (А, В)
Кількість однакових пар виду х (V, W) називається кратністю ребра (V, W).
На рис ребро АС має кратність, що дорівнює 3, а ребро АВ кратність, що дорівнює 2.
2. Число ребер інцидентних вершині А, називається ступенем цієї вершини і позначається deg (A) (від англ. Ступінь).
Якщо вершині инцидентна петля, то вона дає внесок в ступінь, що дорівнює двом, так як обидва кінці приходять в цю вершину.
На рис deg (A) = 5, deg (В) = 2, deg (С) = 3
Вершина графа, що має ступінь, рівну нулю, називається ізольованою.
Граф, що складається з ізольованих вершин, називається нульовим графом. Для нуль-графа Х = Ø.
Вершина графа, що має ступінь, рівну 1, називається висячої
У графі G (V, E) сума ступенів усіх його вершин - число парне, рівне подвоєному числу ребер графа:
де n = V-число вершин, m = X-число ребер графа.
Вершина називається парної, якщо її ступінь - парне число.
Вершина називається непарної, якщо її ступінь - непарне число.
На рис вершина В-парна. а вершини А і С - непарні.
Число непарних вершин будь-якого графа - парне.
Слідство. Неможливо накреслити граф з непарним числом непарних вершин.
4. Граф, в якому не побудовані всі можливі ребра, називається неповним графом
Граф, в якому будь-які дві його різні вершини з'єднані одним і тільки одним ребром, називається повним графом.
Повний граф визначається тільки своїми вершинами
Якщо повний граф має n вершин, то він буде мати
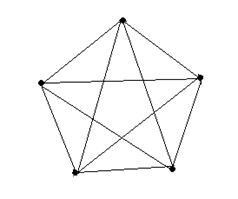
на рис повний граф