Після відкриття надпровідності було зроблено безліч спроб пояснити настільки незвичайні ефекти надпровідності. Серед цих робіт багато теорій досі зберегли своє значення. Так, в 1935 р Ф. і Г. Лондони, використовуючи дворідинної модель, отримали так звані рівняння Лондонов. пояснюють багато макроскопічні властивості надпровідників.
У 1950 р В.Л. Гінзбург і Л.Д. Ландау побудували теорію надпровідності, засновану на квантовій механіці. Рішенням рівнянь Гінзбурга - Ландау були пояснені і передбачити багато властивостей надпровідників, в тому числі ідеальний диамагнетизм, квантування магнітного потоку і ряд інших.
Незважаючи на те, що теорія Гінзбурга - Ландау, що отримала подальший розвиток в роботах А. А. Абрикосова і Л. П. Горькова, описувала багато властивостей надпровідників, воно не могла пояснити явища надпровідності на мікроскопічному рівні.
Купер показав, що при наявності між електронами тяжіння, навіть як завгодно малого, нормальний стан багатоелектронної системи стає нестійким через процес спарювання. Електрони з протилежними імпульсами і антипаралельними спинами об'єднуються в куперовские пари. володіють меншою енергією, ніж окремі нормальні електрони.
Розглянемо, як здійснюється тяжіння між електронами - однойменно зарядженими частинками. Кристалічна решітка складається з позитивних іонів, які притягують електрони. Але і електрони притягають іони, зміщуючи їх від положення рівноваги. Цей зсув незначно внаслідок величезної різниці мас іона і електрона, але воно існує: як кажуть, решітка поляризується. Таке зміщення зарядів порушує однорідність поля іонів і може бути інтерпретовано як поява позитивного заряду. Цей віртуальний заряд притягує інший електрон, що знаходиться поблизу. Область поляризації решітки не є нерухомою, вона переміщається разом з електроном, який її формує. Якщо таке тяжіння буде переважати над кулоновским відштовхуванням, то електрони утворюють пари. Взаємодія електронів через решітку можна уявити як результат випускання фонона одним електроном і поглинання іншим (рис. 5.11, а).
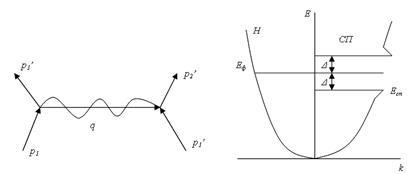
Мал. 5.11. Освіта куперовских пар: а - випускання і поглинання електронами
фонона; б - спектр надпровідника
Нехай Т = 0ДО і фонони решітки в кристалі відсутні. Перший електрон з імпульсом випускає фонон q. який поглинається другим електроном. Електрони після взаємодії змінюють імпульси на і. При цьому виконується закон збереження імпульсів
або, відповідно, для хвильових векторів
де. - хвильові вектори електронів до взаємодії;
. - вектори після взаємодії.
Фонон q. про який йде мова - незвичайний, віртуальний фонон. На відміну від звичайного, він не переміщається вільно по решітці, а тільки від одного електрона до іншого. Як ми вже відзначали, при нульовій температурі звичайних фононів в решітці немає.
Оскільки куперівська пара містить електрони з антипаралельними спинами, вона має нульовий спін і є бозоном. Згідно з розподілом Бозе - Ейнштейна все пари займають рівень ЕФ - # 916; (Рис. 5.11, б). На малюнку для порівняння показані енергетичні спектри нормальної (ліва частина) і надпровідної фаз. Як можна бачити в СП-стані енергетичний спектр має щілину шириною, рівній енергії зв'язку пари 2 # 916 ;. При Т ≈ 0 ширина енергетичної щілини максимальна і дорівнює
де k - постійна Больцмана.
Існування енергетичної щілини отримало експериментальне підтвердження, зокрема, при дослідженні спектра поглинання надпровідника в далекій ІЧ області. При частоті, для якої h # 957; = 2 # 916 ;. починається інтенсивне поглинання випромінювання. Енергія 2 # 916; витрачається на розрив пари. При підвищенні температури також можливі перехід електронів через щілину і освіту над нею неспарених електронів. Величина щілини при цьому зменшується і при Т = ТСщель зникає.
Поблизу ТС енергетична щілину змінюється зі зміною температури, відповідно до виразу
Оцінимо розміри куперовской пари # 958; 0 і їх частку nS в загальній кількості електронів. Для типових значень СП: ЕФ = 10 еВ, КФ = 10 8 см -1 і ТС = = 10К отримуємо # 958; ≈ 10 -4 см. Це означає, що електрони в парі рознесені на 10 3 ... 10 4 періодів кристалічної решітки.
Концентрацію куперовских пар при Т = 0ДО можна визначити інтегруванням виразу (5.70). Вона становить 10 -4 від загальної концентрації вільних електронів. При підвищенні температури ця концентрація убуває і при Т = ТС nS = 0.
Як уже зазначалося, на відміну від окремих електронів - фермионов, куперовские пари є бозонами. Для них не існує постулату заборони Паулі, тобто куперовские пари знаходяться в одному стані і відповідають один одному за всіма фізичними параметрами. Хвильові функції СП електронів є когерентними, тобто їх фази відрізняються один від одного на постійну величину. Таким чином, куперовские пари ( "бозе-конденсат") представляють собою взаємопов'язаний ансамбль.
В електричному полі куперовские пари будуть прискорюватися, тобто отримувати результуючий імпульс через взаємозв'язку між парами. Цей імпульс повинен бути абсолютно однаковим для всіх пар. Однак пара не може обмінюватися енергією з гратами, інакше вона перейде в інше енергетичний стан, що заборонено умовами моделі. Образно кажучи, ансамбль приймає на себе це взаємодія, і, поки воно не велике, повний імпульс ансамблю зберігається, тобто електричний струм не змінюється. Це означає, що перенесення заряду через решітку здійснюється без опору.
Якщо енергія впливу стає більше, ніж енергія зв'язку (Т> ТС. J> jC. В> ВС), тоді зв'язок пари зруйнується і вона залишає квантовий бозе-конденсат.
Теорія БКШ обгрунтувала багато емпіричні співвідношення в надпровідності.
Вище ми розглядали властивості звичайних низькотемпературних надпровідників (див. Табл. 5.1). Тут необхідно сказати про основні відмінності, які мають ВТНП.
1. Високе значення температури переходу лежить в області азотних температур (Т> 77К), що чи не пояснюється існуючою теорією БКШ.
2. Хімічні зв'язку ВТНП. На відміну від НТСП, які володіють металевою (метали, сплави) або ковалентним хімічним зв'язком (напівпровідники), ВТНП є оксиди. Характер зв'язку призводить до того, що в таких надпровідниках концентрація носіїв менше.
3. Нормальне питомий опір (Т> ТС) ВТНП сполук значно більше. ніж у звичайних металів, і сильно залежить від вмісту кисню.
4. На відміну від звичайних НТСП, де температурний перехід займає максимум 1 ... 2К, в ВТНП цей перехід більш 4К і залежить від способу приготування зразка
5. Довжина когерентності Гінзбурга-Ландау в НТСП становить
10 -6 м. Для ВТНП ця величина значно менше - 0,5 ... 30Аº. Нагадаємо, що довжина когерентності характеризує відстані, на яких змінюється щільність надпровідних пар. Таке мале значення довжини когерентності в ВТНП призводить до незвичайних явищ. Зокрема, двовимірні (поверхневі) дефекти в ВТНП можуть утворювати джозефсоновские бар'єри.
Ці та інші зауваження дозволяють зробити висновок про те, що процеси в ВТНП подібні традиційним, однак існують відмінності, пов'язані, в основному, з малою довжиною когерентності, великою глибиною проникнення магнітного поля і т.д. які необхідно враховувати при проектуванні приладів ВТНП мікроелектроніки. Деякі можливі додатки ефектів надпровідності в кріомікроелектроніке будуть розглянуті нижче (п. 10.2).