Теорія ігор розроблена для вирішення конфліктних ситуацій. тобто ситуацій, в яких стикаються інтереси двох і більше сторін, що переслідують різні цілі.
Якщо цілі сторін прямо протилежні, то говорять про антагоністичному конфлікті.
Грою називається спрощена формалізована модель конфліктної ситуації.
Одноразовий розіграш гри від початку до кінця називається партією. Результатом партії являетсяплатёж (ілівиігриш).
Партія складається з ходів. тобто виборів гравців з деякого безлічі можливих альтернатив.
Ходи можуть бути особисті іслучайние .Лічний хід. на відміну отслучайного. передбачає свідомий вибір гравцем певного виду.
Ігри, в яких є хоча б один особистий хід, називаються стратегічними.
Ігри, в яких всі ходи випадкові, називаються азартними.
При здійсненні особистого ходу говорять також про стратегію гравця, тобто про правило або сукупності правил, що визначають вибір гравця. При цьому стратегія повинна бути всеосяжною, тобто вибір повинен бути визначений для будь-якої можливої в ході партії ситуації.
Завдання теорії ігор - знаходження оптимальних стратегій гравців, тобто стратегій, що забезпечують їм максимальний виграш або мінімальний програш.
Класифікація теоретико-ігрових моделей
Гру n осіб прийнято позначати як, де
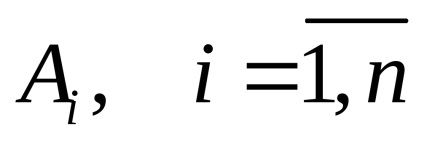
Відповідно до цього позначенням можна запропонувати таку класифікацію теоретико-ігрових моделей:
Дискретні (безлічі стратегій

Безперервні (безлічі стратегій

Антагоністичні (гри з нульовою сумою)
(Інтереси сторін протилежні, тобто програш одного гравця дорівнює виграшу іншого)
З повною інформацією (якщо гравцеві, котрий робить особистий хід відома вся передісторія гри, тобто всі ходи противника)
З неповною інформацією
З нульовою сумою (сумарний платіж дорівнює нулю)
З ненульовою сумою
Матричне подання парної антагоністичної гри
В даному посібнику будемо розглядати антагоністичні гри двох осіб. задані в матричної формі. Це означає, що нам відомо безліч стратегій першого гравця (ігрокA) Ai>, i = 1, ..., m і безліч стратегій другого гравця (ігрокB) Bj>, j = 1.n. а також задана матріцаA = || aij || виграшів першого гравця. Оскільки мова йде про антагоністичної грі, то передбачається, що виграш першого гравця дорівнює програшу другого. Вважаємо, що елемент матріциaij - виграш першого гравця при виборі їм стратегііAi і відповіді йому другого гравця стратегіейBj. Таку гру будемо позначати як
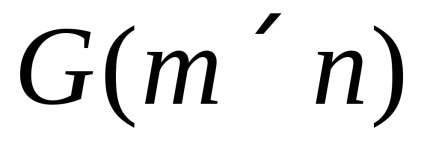
Неважко бачити, що дана гра є антагоністичною, крім того, вона є грою з неповною інформацією, тому що гравцеві В, який робить особистий хід, невідомо, який вибір зробив гравець.
Як зазначалося вище, завдання теорії ігор полягає в знаходженні оптимальних стратегій гравців, тобто стратегій, що забезпечують їм максимальний виграш або мінімальний програш. Цей процес називається рішенням гри.
При вирішенні гри в матричної формі слід перевірити гру на наявність сідлової точки. Для цього вводяться дві величини:
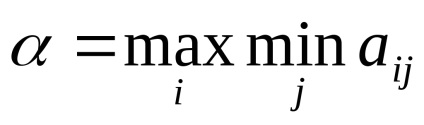
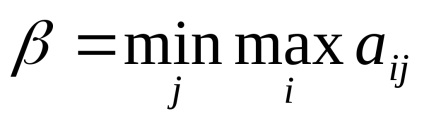
Перший гравець, швидше за все, вибере ту стратегію, при якій він отримає максимальний виграш серед усіх можливих відповідей другого гравця, а другий - навпаки, ту, яка мінімізує його власний програш, тобто можливий виграш першого.
Можна довести, що α ≤V≤ β. гдеV-ціна гри. тобто ймовірний виграш першого гравця.
Якщо виконується співвідношення α = β = V. то кажуть, чтоігра має седловую точку
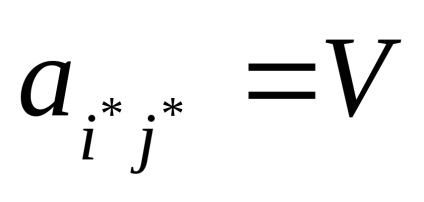
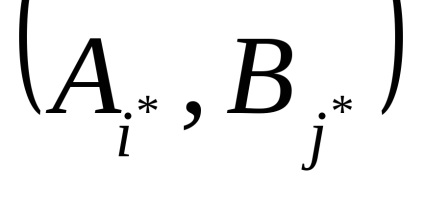
Повернемося до гри, розглянутої нами в прикладі 1 і перевіримо її на наявність сідлової точки.
Ця гра - з повною інформацією.
В даному випадку
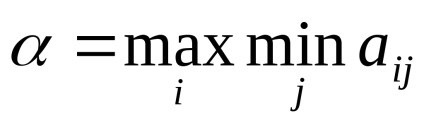
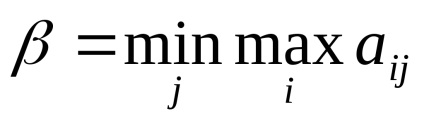
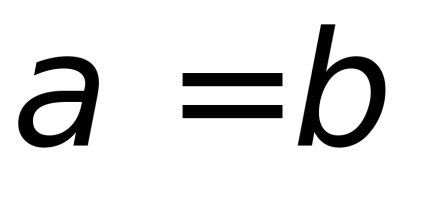
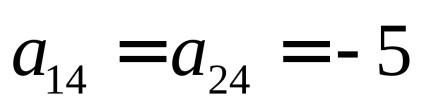
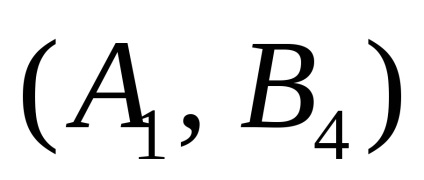
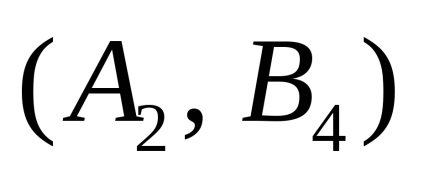
Приклади 2 і 3 є непоганою ілюстрацією до наступній теоремі, доведеною в теорії ігор:
Будь-яка парна антагоністична гра з повною інформацією вирішується в чистих стратегіях.
Т.ч. теорема 1 говорить про те, що будь-яка гра двох осіб з повною інформацією має седловую точку і існує пара чистих стратегій
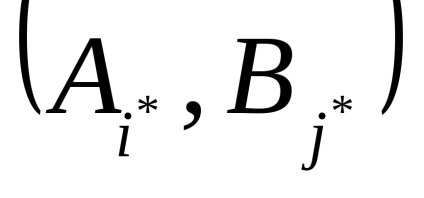
Уразі ж відсутності сідлової точки, як рішення використовуються т.н.смешанние стратегії:, гдеpiіqj - ймовірності вибору стратегійAi і Bj першим і другим гравцями відповідно. Рішенням гри в даному випадку є пара змішаних стратегій
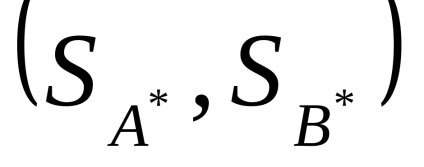
Узагальненням теореми 1 на випадок гри з неповною інформацією служить наступна теорема:
Будь-яка парна антагоністична гра має хоча б одне оптимальне рішення, тобто пару в загальному випадку змішаних стратегій
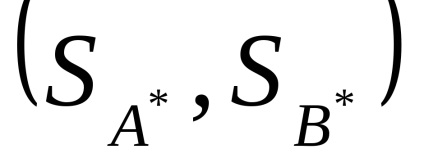
В окремому випадку, для гри з сідловою рішення в змішаних стратегіях виглядає як пара векторів, в яких один елемент дорівнює одиниці, а інші рівні нулю.