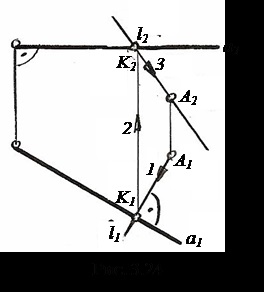
З теореми про окремий випадок проектування прямого лінійного кута (див. Рис. 1.10) випливає, що якщо одна сторона прямого лінійного кута паралельна будь-якої площини проекцій, то на цю площину прямий кут спроецируется в натуральну величину.
3.5.2. Перпендикулярні пряма і площина. Як відомо, пряма перпендикулярна до площини, якщо вона перпендикулярна до двох пересічних прямих, які лежать в цій площині.
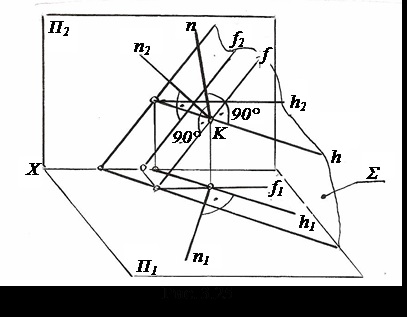
Нехай необхідно (рис. 3.25) з точки K # 931; силу поставити перпендикуляр n ^ # 931; .
Для цього через точку K проведемо горизонталь h і фронталь f і перпендикулярно до них проведемо пряму n (n # 9524; h і n # 9524; f).
На підставі теореми про окремий випадок проектування прямого лінійного кута кут між n і h на # 928; 1 спроецируется без спотворення, тобто кут між горизонтальною проекцією горизонталі h1 і горизонтальною проекцією перпендикуляра n1 буде прямим (n1 # 9524; h1).
Аналогічним чином можна довести, що якщо n # 9524; f. то n2 # 9524; f2. де
f2 - фронтальна проекція фронталі.
Отже, якщо пряма перпендикулярна до площини, то її проекції перпендикулярні до однойменних проекцій однойменних ліній рівня. тобто якщо n # 9524; # 931; (H∩f), то n1 # 9524; h1 і n2 # 9524; f2.
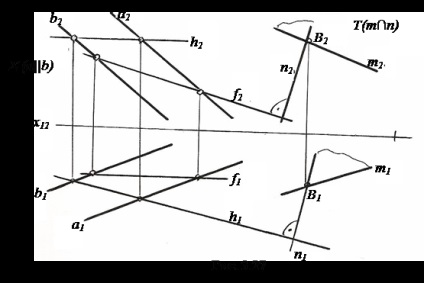
Нехай потрібно з точки K (K1, K2) відновити перпендикуляр до площини # 931; (A || b) (рис. 3.26, а).
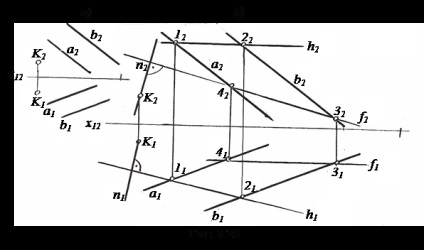
3.5.3. Перпендикулярні площині. Дві площини взаємно перпендикулярні, якщо одна з них проходить через пряму лінію, перпендикулярну інший. Тому при проведенні площині, перпендикулярній до іншої площини, спочатку будують пряму, перпендикулярну до площини, і потім укладають її в будь-яку площину.
На рис. 3.27 через точку B проведена площину T (m∩n) перпендикулярно # 931; (A || b).
Побудована площину T (m∩n) буде перпендикулярна # 931 ;.