геометричні зв'язку
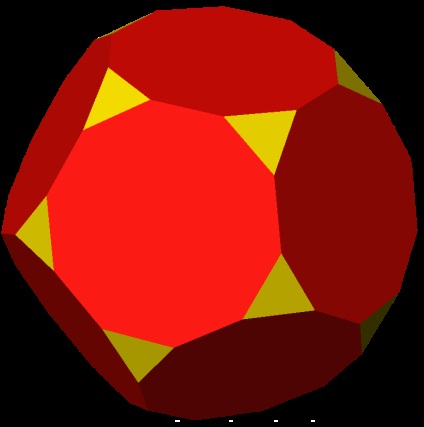
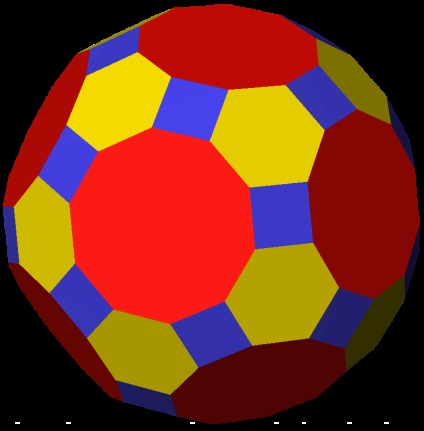
Плосконосий додекаедр може бути отриманий з дванадцяти правильних п'ятикутних граней Додекаедр шляхом їх витягування назовні [en]. так що вони перестають торкатися один одного. При витягуванні на відповідне відстань це дасть ромбоікосідодекаедр. якщо заповнити отримане простір між розділеними ребрами квадратами, а між розділеними вершинами - трикутниками. Але щоб отримати плосконосий вид, заповнюємо тільки трикутні грані, квадратні проміжки залишаємо порожніми. Тепер повертаємо п'ятикутники щодо їх центрів разом з трикутниками, поки квадратні проміжки не перетворяться в рівносторонній трикутники.
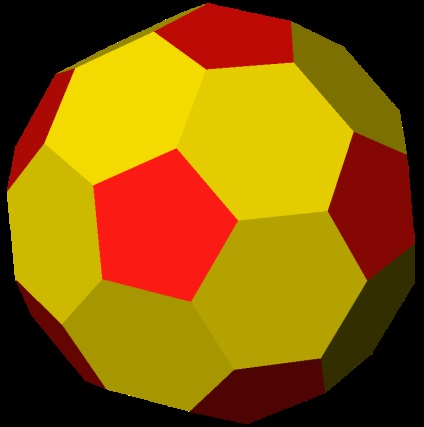
Плосконосий додекаедр можна також отримати з ромбоусечённого ікосододекаедр шляхом альтернаціі [en]. Шістдесят вершин ромбоусечённого ікосододекаедр утворюють багатогранник, топологічно еквівалентний одному Плосконос додекаедрів. Решта шістдесят утворюють його дзеркальне відображення. Одержаний багатогранник вершинно транзітіва [en]. але не однорідний, оскільки має ребра різної довжини, необхідна деяка деформація, щоб привести його до однорідного багатограннику.
Пов'язані багатогранники і мозаїки
Сімейство однорідних ікосаедральних багатогранників





Напишіть відгук про статтю "Плосконос додекаедр"
Примітки
література
- Weisstein, Eric W. [mathworld.wolfram.com/SnubDodecahedralGraph.html Snub dodecahedral graph] (англ.) На сайті Wolfram MathWorld.
- [Mathworld.wolfram.com/GreatRhombicuboctahedron.html 3D convex uniform polyhedra]
- [Www.dr-mikes-math-games-for-kids.com/polyhedral-nets.html?net=aDiAd7EuD6JEyMy1JVKFsa8iDW5tM3Qs3MqxBVGvmd0694UNAzjcvcRXcqBcC0KGnIBi7h9Cg3w8ikfFW8uoxM4d8N02mUmiPtVdjRPES3K1YArAm20bjfn9nWCHZyBubfS1uMff57mXxR7FJJfAfnu4OcLgXVVXORgYnVJIjjFwCcT2i1hLxuYbchkA5VGUKE1Xrvjw5arGCHafH9uIWvTT0ZGeb7LJ5C90hu7ALyKfc9C7vxnyqc2dVwmoXQSD9kc84xzoZiGGWx4MyhCpjnD5MVLpy8LssafhN1eSm2ZrUT4snKGowFy8b3ZbTsWtLD0HPNYfZWrbvpgWhE4ToCjGOOKXWnUT3qflcKZLGxwRrv5gWaxKZeBPQNwvRohjtyI96MJL5N1lz9FLKmEQbwliTaWaqBK7aWIiuMjhMxo3QghFTa1mLqvtZFll4OOyKnnjWe3uWAW0AX6tYWUEhElXF1f5QM9zSeKxr80WxlOQUXS875Be7s7cirEkBwiwTzNbQkQCjC3UlMHw05WygS2LQzqhxoLVDIW43poA7RxsZzZ54x9kBmVeMuZDYJPVFPGFJiOOHk2SwSMB1E4UmlEZb2LKxNr19bc3YnVn06RJjG2F5y5pbzKdyq1J0tZ5aX7Mi61LcreSoHOrO5teQDDQL7bkqcPixbpxQCSmX7jVCGFzLqgZF3c9t56VBAmM8FcRname=Snub+Dodecahedron#applet Editable printable net of a Snub Dodecahedron with interactive 3D view]
- [Www.mathconsult.ch/showroom/unipoly/ The Uniform Polyhedra]
- [Www.georgehart.com/virtual-polyhedra/vp.html Virtual Reality Polyhedra] The Encyclopedia of Polyhedra
- [Www.mocpages.com/moc.php/253958 The Snub Dodecahedron made with LEGO] by Antonio Nicassio (ITALY)
Для поліпшення цієї статті бажано? :
- Перевірити якість перекладу з іноземної мови.
- Виправити статтю згідно стилістичним правилам Вікіпедії.