Віртуальна лабораторна робота № 8
"ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ТЕРТЯ"
Теоретичні основи роботи.
Основною метою роботи є визначення коефіцієнта тертя між колесами візка і рейками. Будемо вважати, що колеса під час руху вагонетки обертаються без прослизання. У цьому випадку коефіцієнт тертя називають коефіцієнтом тертя кочення. В основу розрахунку цієї величини в даній роботі покладено фундаментальний закон фізики: закон збереження імпульсу і закономірності, пов'язані з переходом одного виду енергії в інший. Розглянемо застосування цих закономірностей на представленої моделі зіткнення гарматного ядра і вагонетки з вантажем. Після пострілу, гарматне ядро і вагонетку можна вважати замкнутою системою, загальний імпульс якої повинен завжди залишатися постійним і рівним нулю. Так як ядро після попадання в вагонетку застряє в ній, вважаємо взаємодію цих тіл абсолютно непружним. Напишемо закон збереження імпульсу для цього випадку в скалярному вигляді:
де M- маса вагонетки з вантажем, m- маса гарматного ядра, v- швидкість польоту ядра, u- загальна швидкість руху тіл після взаємодії. Ліва частина рівняння (1) є імпульсом системи до взаємодії, який складається тільки з імпульсу рухається ядра, так як вагонетка нерухома. Права частина рівності - це імпульс системи після взаємодії - ядра і вагонетки, які рухаються з однаковою скоростьюuравной:
Тепер уважно розглянемо енергетичні співвідношення. Якщо система тіл після непружного взаємодії має швидкість не рівну нулю, отже, ця система має кінетичної енергією Еkc. яку можна визначити як:
До зіткнення кінетичної енергією володіло тільки одне ядро і ця енергія дорівнює Ekя =
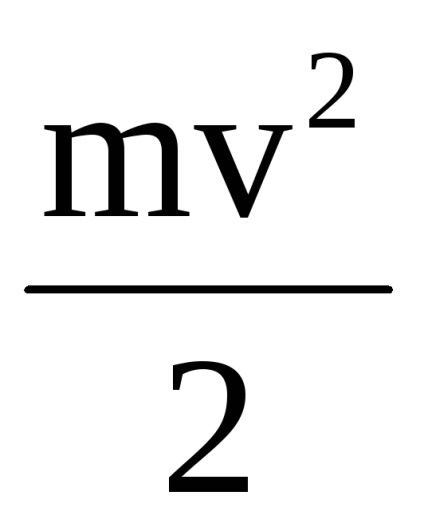
вираз
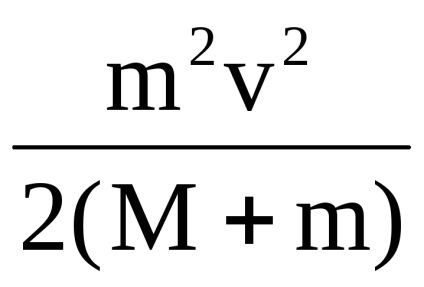
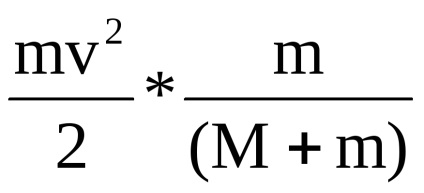
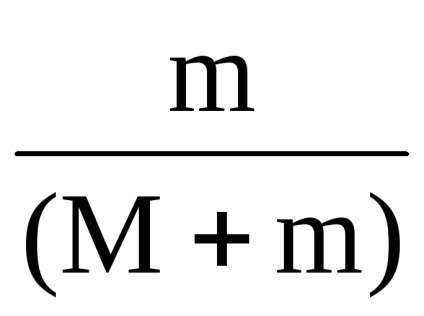
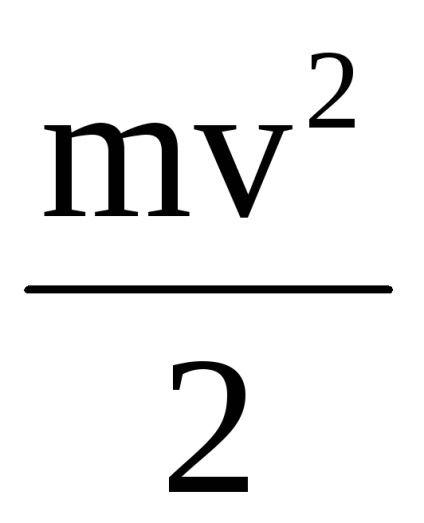
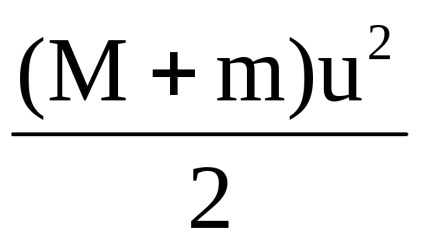
де Q-величина, що характеризує енергію, яка перейшла в нагрів тіл і деформацію. Отже, повна механічна енергія ядра нікуди безслідно не зникла, а перейшла в кінетичну енергію системи тіл і внутрішню енергію цієї ж системи.
Після потрапляння ядра в вагонетку система тел стала рухатися, але тепер розглядається система не замкнута, так як в ній діють неконсерватівние сили тертя, в результаті дії яких вагонетка зупиниться. Дія таких сил повністю еквівалентно впливу на нашу систему зовнішніх сил. Куди подінеться кінетична енергія системи Еkc цих тіл після зупинки? Відповідь на це питання укладений в усвідомленні того, що якщо система не замкнута, повна механічна енергія буде зменшуватися, а величина, що характеризує зміну енергії в механіці, це робота. Тепер ми можемо сказати, що кінетична енергія незамкненою системи тел ядро - вагонетка змінилася від значення
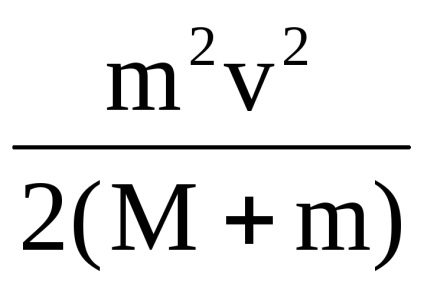
В даному випадку силу тертя на всьому шляху руху вагонетки будемо вважати постійною. Остаточним результатом роботи сил тертя, знову ж таки, можна вважати збільшення внутрішньої енергії тіл, що стикаються поверхнями, що труться. Механічну роботу в нашому прикладі можна уявити як:
S- шлях, пройдений вагонеткою до остановкі.Fтр = kN, гдеk- коефіцієнт тертя, N- сила нормального тиску вагонетки на рейки. При горизонтальному русі ця сила дорівнює силі тяжіння: N = (M + m) g. Уявімо тепер рівність (6) з урахуванням значення всіх величин і (7):
Остаточно отримаємо для коефіцієнта тертя:
Опис комп'ютерної моделі установки.
Після завантаження програми на екрані монітора з'явиться старовинне знаряддя, вагонетка і кнопки управління. Вагонетка стоїть на рейках, з якими сполучена шкала відстаней, і по якій можна визначити величину відкату вагонетки після потрапляння в неї ядра. Інформація про маси ядра, вагонетки і швидкості польоту ядра представлена у верхніх рядках екрану, і треба відзначити, що при кожному запуску програми ці маси можуть змінюватися, а при кожному пострілі швидкість вильоту снаряда із ствола гармати змінюється. Коефіцієнт тертя також призначається комп'ютером як випадкова величина, тому для кожного студента, що виконує дану роботу, він може відрізнятися. Вагонетка після попадання ядра буде переміщатися на деяку відстань, яке буде визначатися величинами мас, швидкістю вильоту ядра і коефіцієнтом тертя. При кожному пострілі ця швидкість буде також різною. Для вимірювання відстані відкоту вагонетки скористайтеся покажчиком, прикріпленим до неї, який Ви побачите у вигляді стрілки на початку вагонетки. Ціна маленького поділу шкали відстаней дорівнює 0.1 м. Відзначивши положення вагонетки до пострілу і після пострілу, Ви зможете визначити, на яке відстані відкотиться вагонетка з вантажем і ядром після пострілу. Повідомлення на кнопках не вимагає особливих пояснень і вони зрозумілі для кожного користувача. Якщо після пострілу вагонетка відкотиться за межі екрану, то таку спробу не треба враховувати.
Знайдіть на екрані монітора значок "Робота № 8" і клацніть лівою клавішею мишки по ньому два рази поспіль. На екрані монітора з'явиться модель експерименту, яку в природі, до речі, здійснити досить складно. Запишіть в таблицю вимірювань значення маси ядра і вагонетки з вантажем. Ці значення під час експерименту змінюватися не будуть, якщо ви не перезавантажте програму. Тепер приступайте до експерименту.
1. Запишіть у таблицю вимірювань швидкість вильоту ядра з ствола гармати в першому випадку. Відзначте у себе в чернетці положення візира вагонетки за шкалою відстаней і прийміть це значення за умовний нуль.
2. Натисніть на кнопку пуск. Відбудеться постріл і вагонетка відкотиться на якийсь відстань. Відзначте це положення і визначте Sрасстояніе відкату вагонетки. Запишіть величину відкату в таблицю вимірювань в графу відповідної даної швидкості вильоту ядра. Поверніть вагонетку на колишнє місце.
3. Проведіть 5-6 пострілів, кожен раз записуючи величину швидкості і відстані відкоту вагонетки. Підпишіть результати вимірювань у викладача. Тепер в лабораторії або будинку приступайте до розрахунків.
4. За формулою (9) розрахуйте коефіцієнт тертя для кожного пострілу, записавши результати в відповідну графу таблиці.
5. Для розрахунку абсолютної похибки скористайтеся алгоритмом прямих багаторазових вимірювань.
6. Округлите похибка і результат, записавши їх у встановленій формі.