Криву лінію можна розглядати як траєкторію руху точки на площині або в просторі, а також як сукупність точок, що задовольняють певному рівнянню. Крива лінія може бути результатом перетину між собою кривих поверхонь або кривої поверхні і площини.
Криву лінію називають плоскою, якщо всі крапки лінії лежать в одній площині (коло, еліпс, парабола), і просторової, якщо точки не належать одній площині (гвинтова лінія).
Еліпс: для побудови еліпса проводять дві концентричні кола, діаметри яких дорівнюють осях еліпса. Ці кола ділять на 12 рівних частин. Через точки поділу на великий окр. проводять вертикальні лінії, через відповідні точки поділу на малій окр. - горизонтальні лінії. Перетин цих ліній дасть точки еліпса.
Парабола: нехай дано вершина параболи О, одна з точок параболи D і напрямок осі ОС. На відрізках ОС і СD будують прямокутник, сторони цього прямокутника ОВ і ВD ділять на однакове число рівних частин і нумерують точки ділення. Вершину Про з'єднують з точками ділення боку BD, а з точок поділу відрізків ОВ проводять прямі, паралельні осі. Перетин прямих, що проходять через точки з однаковими номерами, визначає ряд точок параболи.
Циклоїда: Троекторія точки А, що належить колу радіуса R, перекочується без ковзання по прямій, називається циклоїдою. Для її побудови від початкового положення точки А на направляючої прямий відкладають відрізок Аа1, Рівний довжині даної окружності 2πR. Коло та відрізок Аа1 ділять на однакові число рівних частин.
Востанавлівая перпендикуляри з точок деленгія прямий Аа1 до перетину з прямою, що проходить через центр даного кола паралельно Аа1. намічають ряд послідовних положень центру перекочувати окружності О1, О2, О3 ... .О8.
Описуючи з цих центрів кола радіуса R, відзначають точки перетину з ними прямих, що проходять паралельно Аа1 через точки поділу кола 1,2,3,4 і т.д.
У перетині горизонтальної прямої, що проходить через точку 1, з окружністю, описаної з центру О1, перебувати одна з точок циклоїди; в перетині прямої. що проходить через точку 2, з окружних, перекладеної з центру О2. перебувати інша точка циклоїди і т.д.
Синусоїда (рис. 7.4 б). для побудови синусоїди ділять окружність заданого радіуса R на рівні частини (6,8,12 і т.д.) і на продовженні осьової лінії від умовного початку-точки А-проводять відрізок АВ, рівний 2πR. Потім пряму ділять на таке ж число рівних частин. що і окружність (6,8,12 і т.д.) З точок кола 1,2,3 ... 12 проводять прямі лінії паралелльно обраної прямий до перетину з відповідними перпендикулярами, відновлення або опущеними з точок поділу прямої.
Отримані точки перетину (1,2,3 ... 12) і будуть точками синусоїди з пекріодом коливань, рівним 2πR.
Евольвента (розгортка кола). Евольвентою (ріс.7.4в) називаеться траєкторія, що описується точкою прямої лінії, перекочуються по колу без ковзання.
У машинобудуванні за евольвенті окреслюють профіль головок зубів зубчастих коліс.
Для побудови евольвенти окружність радіуса R попередньо ділять на довільне число n рівних частин; в точках поділу проводять дотичні до кола, нарпавленние в одну сторону.На дотичній, проведеної через останню крапку поділу, відкладають відрізок, рівний дліге окрудності 2πR, і ділять його на те ж число n рівних частин.
Відкладаючи на першій касательноий одну поділку, рівне 2πR, а на другий-два, на третій- три і т.д. отримують ряд точок I, II, III, IV і т.д. які з'єднують за лекалом.
Сполученням називають плавний перехід з кола на пряму або з кола на коло. геометричній основою сполучень є положення про геометричні місцях точок. Перпендикуляр, проведений до відрізка через його середину, є геометричним місцем точок, рівновіддалених від його кінців. ГМТ, рівновіддалених від прямої в площині, є дві прямі, паралельні заданій прямій і віддалені від неї на задану відстань. ГМТ, рівновіддалених від окружності, є дві концентричні кола, радіуси яких збільшені або зменшені на задану величину в порівнянні з радіусом вихідної окружності. ГМТ, рівновіддалених від сторін кута, є його бісектриса. ГМТ, що лежать в площині і рівновіддалених від точки на задану відстань, є окружність цього радіусу
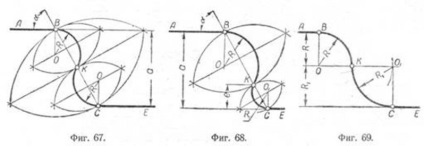
Сполучення паралельних прямих
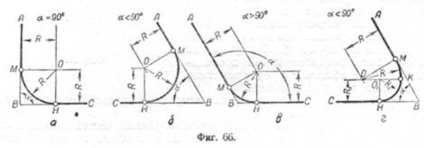
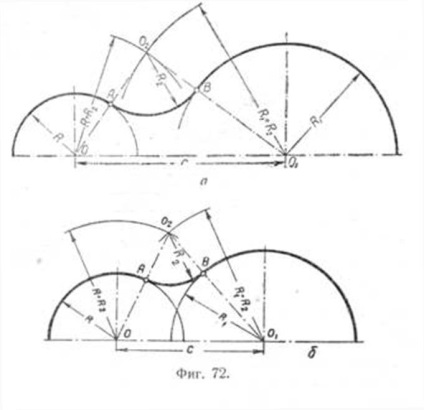
Сполучення пересічних прямих
23. Аксонометріческіе проекції: принципи освіти, изометрия, діаметром, триметр. Стандартні аксонометричні проекції (косокутні, прямокутні).
Залежно від напрямку проектують променів аксонометричні проекції поділяються на: прямокутні або ортогональні (проектують промені перпендикулярні аксонометрической площині) і косокутні (проектують промені нахилені до аксонометрической площині).
Аксонометріческіе проекції - це наочні зображення, що володіють метричної визначеністю. Ізометрична проекція - аксонометрична проекція, при якій довжини одиничних відрізків на всіх трьох осях однакові. Діметріческая проекція - це аксонометрична проекція, у якій по двох осях відкладають рівні значення, а по третій відкладають значення скорочена в два рази. Триметр - аксонометрична проекція, у якій вимір по всіх трьох осях різне.