Плоскою кривою лінією називається лінія, кожна точка якої належить одній площині. В іншому випадку крива лінія називається просторової (гвинтова лінія, лінії перетину двох поверхонь, з яких хоча б одна є кривою поверхнею).
Закономірні лінії описуються рівняннями і діляться на алгебраїчні другого і вищого порядків і трансцендентні, описувані тригонометричними функціями. Порядок кривої лінії - це ступінь її рівняння або кількість точок перетину кривої лінії з прямою лінією (для плоских кривих) або кількість точок перетину з площиною (для просторових ліній). Криві другого порядку іноді називаються кониками.
Коробовим лініями (або обводами) називаються складові криві лінії, дуги яких послідовно визначені парами точок обвода. Якщо на стиках можна побудувати загальну дотичну, то обвід називається гладким. Циркульними лініями називаються лінії, побудова яких можна здійснити циркулем (овал, овоід, завиток і ін.).
Лекальними кривими називаються плоскі закономірні лінії, при кресленні яких використовуються лекала (еліпс, парабола, гіпербола та ін.).
Циклічні криві лінії - це лінії, що повторюються в процесі освіти (циклоїда, епіциклоїда, гіпоциклоїда і ін.).
Гладкі криві лінії складаються з звичайних точок.
Звичайні точки кривої лінії - це точки, в яких можна побудувати тільки одну дотичну до кривої лінії. Якщо крива лінія містить особливі точки, то лінія називається негладкою.
Еквідистантно і еквітангентние лінії - це лінії, рівновіддалені від якоїсь кривої лінії і повторюють її форму.
Апроксимовані лінії - це лінії, наближено замінені
іншими більш зручними для креслення лініями (наприклад, еліпс іноді замінюють овалом).
Плоскі просторові криві лінії
Найбільш часто в техніці застосовуються лекальні криві лінії, які можуть бути плоскими і просторовими. До них відносяться еліпс, парабола, гіпербола, евольвента, циклоїда, гвинтова лінія і інші, приклади яких наведені на малюнку 1. Способи побудови лекальних кривих зазвичай розглядається в курсі технічного
Евольвента - траєкторія точки дотичній, перекочується без ковзання по колу. Іноді її неправильно називають розгорткою окружності.
Синусоїда - крива лінія, описувана рівнянням y = sin x.
Гіпербола - геометричне місце точок, різниця відстаней яких від двох точок, які називаються фокусами, є величина постійна.
Гвинтова лінія - траєкторія точки, що переміщається по котра утворює циліндра, конуса або тора, в той час як сама утворює рівномірно обертається навколо осі згаданих поверхонь.
Еліпс - геометричне місце точок, сума відстаней яких до двох точок, які називаються фокусами, є величина постійна.
Парабола - геометричне місце точок, рівновіддалених від деякої точки, званої фокусом, і деякої прямої, званої директоркою.
Циклоїда - траєкторія точки окружності, перекочується без ковзання по прямій лінії. При побудові епі- і гіпоціклоіди окружність перекочують по колу.
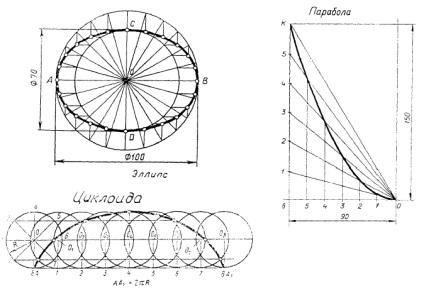
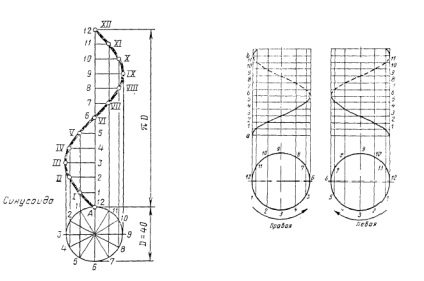
Малюнок 1 - Приклади лекальні кривих
Побудова проекцій кривої лінії
Проекції кривої лінії мають такі властивості:
У загальному випадку проекція кривої лінії є крива лінія;
Якщо точка належить кривій лінії, то її проекції
належать однойменною проекція кривої;
Дотична до кривої лінії проектується в дотичну до
проекція кривої лінії.
ПРИКЛАД 1. Побудувати проекції правої циліндричної гвинтової лінії, що проходить через точку поверхні циліндра.
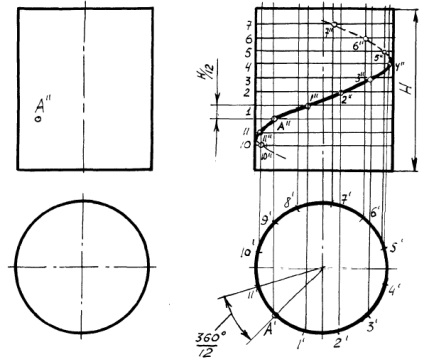
Малюнок 2 - Приклад 1.
РІШЕННЯ . Знаходимо точку A /. Починаючи з точки A /. ділимо окружність підстави циліндра на 12 частин. Висоту циліндра H ділимо на 12 частин, починаючи з точки A //. На перетині вертикальних і горизонтальних однойменних ліній знаходимо точки гвинтовий лінії, які плавно з'єднуємо (малюнок 2).
Загальні відомості про поверхні
Поверхня - це геометричне місце лінії, що рухається в просторі за певним законом. Цю лінію називають що утворює. Вона може бути прямою, тоді утворену їй поверхню відносять до класу лінійчатих. Якщо утворює - крива лінія, поверхня вважають нелінійчатих. Лінію, по якій переміщують утворить, називають направляючої. В якості останньої іноді використовують слід поверхні.
Визначником поверхні називають сукупність умов, які задають поверхню в просторі.
Поверхня вважають заданою, якщо можна побудувати проекції будь-якої її утворює. Одну і ту ж поверхню можна утворити рухом різних ліній. Наприклад, сфера утворюється обертанням кола навколо її діаметра.
Розглянуті нижче поверхні класифіковані в такий спосіб.
I. Поверхні обертання лінійчатих.
II. Поверхні обертання нелінійчатих.
Тор (кругової, параболічний, еліптичний).
Еліпсоїд (витягнутий і стиснутий).
Поверхня обертання загального виду.
III. Поверхні з площиною паралелізму.
IV. Поверхні, що задаються каркасом.
Поверхні обертання лінійчатих
Всі поверхні цього класу утворені обертанням прямої лінії навколо іншої прямої. Дві прямі можуть займати відносно один одного три різних положення. Кожному з них відповідає своя поверхню обертання.
1
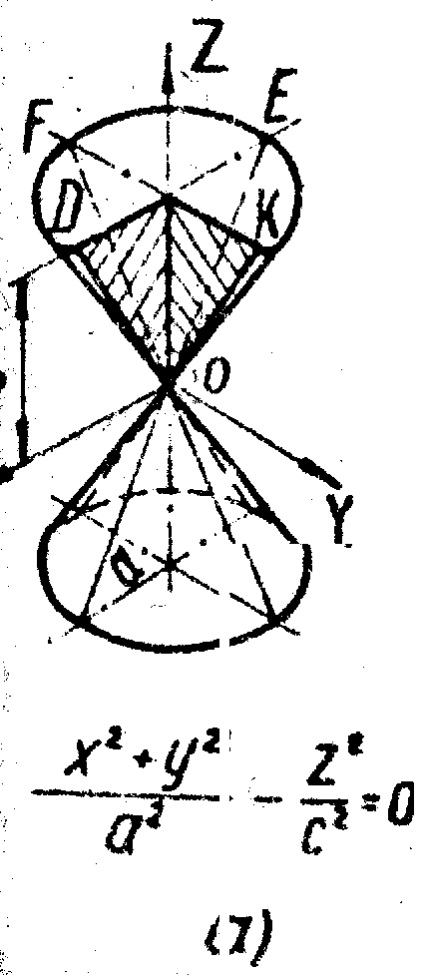
.Конус утворюють обертанням прямої OD навколо пересічної з нею осі Z (рис. 3, а). Координатні площини XOZ і YOZ розсікають конус по пересічним прямим OD, OE, OK і OF; площину XOZ дає в перетині точку О; площину. паралельна XOY, перетинає по колу (DFEK).
Для побудови точки, що належить кривій поверхні, її поверхні маємо на проекціях лінії, що лежить на цій поверхні.
Конус бере участь в утворенні форми діаграми спрямованості антени, поверхні положення об'єкта в просторі, антени і її опромінювача, дифузора гучномовця, резонатора, відбивача радіохвиль, електронно-променевих трубок і електронних ламп, світловода, деталей вакуумних установок і так далі.
2
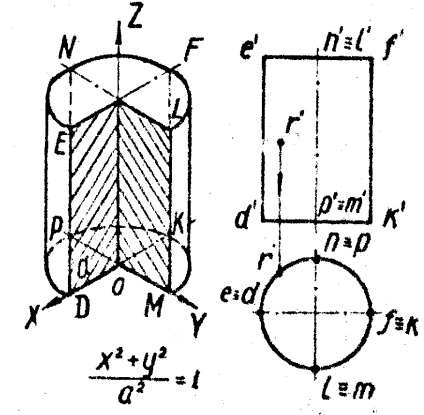
.Циліндр утворюють обертанням прямий ЕD навколо паралельної їй осі Z (рис. 3, б, в)
Площині XOZ і YOZ перетинають його вздовж паралельних прямих ED, FK, NP, LM, а площину XOY і їй паралельні - по колах DPKM і (ENFL).
Циліндр застосовують при утворенні форми хвилеводів, антен, амортизаторів приладів, дзеркал лазерів, корпусів датчиків і так далі.
3.Однополостний гіперболоїд утворюють обертанням прямий ED навколо скрещивающейся з нею осі Z (рис. 4).
Площині XOZ і YOZ перетинають його по гіпербол FK, LM, PQ і RS, а площину XOY і їй паралельні - по колах (GU, FPLR і KQMS). При обертанні точок D і Е їх проекції d і е переміщуються по колу, а проекції d і e - за прямими, паралельним осі Х. Точка U прямий DE, ближче інших розташована до осі обертання, описує окружність UU1 найменшого діаметра. Цю окружність називають горлом поверхні. Промені, які проектують якусь поверхню, стосуються її в точках, що утворюють контурну лінію. Відповідна проекція цієї лінії називається нарисом поверхні.
Форму однополостного гиперболоида імеютнекоторие радіощогли. Він також утворює форму вібраційних живильників, що використовуються в промисловій автоматиці, кулачків, з'єднувачів контактів і так далі.
До цього класу відносять в основному поверхні, утворені обертанням кривих другого порядку.
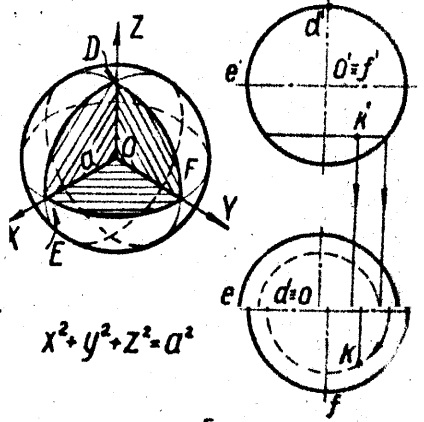
1. Сферу утворюють обертанням окружності навколо її діаметра (рис. 5)
Будь-яка площина перетинає сферу по колу. Нарис фронтальної проекції сфери називають головним меридіаном. нарис горизонтальної проекції - екватором. Проекції точки К, що лежить на поверхні сфери, належать проекція горизонтальної окружності, проведеної на сфері.
Сфера утворює форму діаграми спрямованості антен, обтічника і випромінювача антени, головки мікрофона, контактів реле і так далі. Сфера є поверхнею положення об'єкта в просторі.
2.Круговой тор утворюють обертанням окружності навколо осі, що лежить в площині цієї окружності і що є її діаметром. Таким чином, сферу можна розглядати як окремий випадок тора. Розрізняють тор-кільце. коли вісь обертання не перетинає утворить коло, і тор-бочку.
У радіотехніці використовують також параболічний і еліптичний тор.
Параболічний тор утворюють обертанням параболи навколо прямої, що лежить в площині цієї параболи і що є її фокальній віссю.
Еліптичний тор утворюють обертанням еліпса навколо прямої, що лежить в площині цього еліпса і не є його віссю.
Торовиє поверхні мають діаграми спрямованості антен, поверхні положення об'єкта в просторі, антени і їх обтічники, хвилеводи, резонатори, гучномовці і так далі.
Еліпсоїд утворюють обертанням еліпса навколо його малої або большойосі. У першому випадку отримують стиснений (рис. 6, а), а в другому - витягнутий еліпсоїди обертання (рис. 6, б).
Площині XOZ і YOZ перетинають їх по еліпсам DE і EF, а площину XOY - по колу DF.
Форму еліпсоїда мають дзеркала антен і лазерів, випромінювачі антен, поверхні положення і так далі.
Двуполостной гіперболоїд утворюють обертанням гіперболи DE навколо її дійсної осі FF1 (рис. 7).
Площині XOZ і YOZ перетинають його по гіпербол DE і KE; площину XOY дає в перетині уявну точку О.
Форму його мають дзеркала антен, поверхні положення об'єкта в просторі і так далі.
5.Параболоід утворюють обертанням параболи OD навколо її фокальної осі OF (рис. 8).
Дзеркала антен і лазерів найчастіше виготовляють параболічними.
6.Поверхность обертання загального виду утворюють обертанням довільної кривої.
Поверхні з площиною паралелізму.
Всі поверхні цього класу - лінійчатих.
1.Ціліндроід утворюють переміщенням прямої за двома кривими напрямних, коли утворює залишається паралельної заданої площині. Форму циліндроїда мають деякі об'ємні графіки, застосовувані в теорії оптимального регулювання, а також хвилеводи.
2.Коноід утворюють переміщенням прямий по кривій лінії і прямий, коли утворює залишається паралельної заданої площині. Окремим випадком коноида є прямою гелікоїд, утворений переміщенням прямої по гвинтовий лінії і її осі, коли утворює залишається паралельної заданої площині.
3.Гіперболіческій параболоїд чи косу площину утворюють переміщенням прямої за двома перехресними прямими, коли утворює залишається паралельної деякій площині. Отримана поверхня має седлообразную форму (рис. 9).
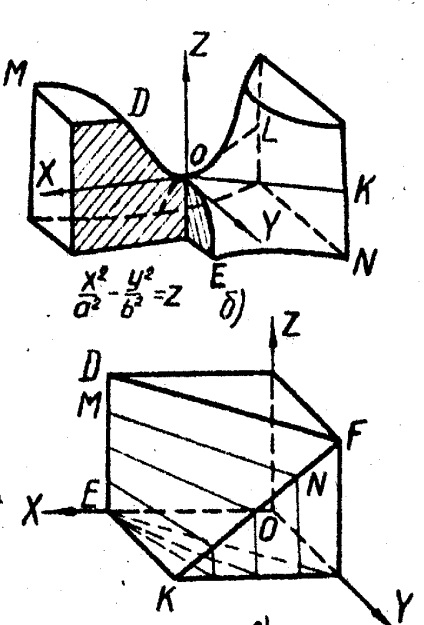
Площині XOZ і YOZ перетинають цю поверхню по парабола OD і OE; площині паралельні XOZ і YOZ, також дають в перетині параболи; площину XOZ перетинає поверхню по двом пересічним прямим OL і OK, а площині, паралельні XOZ, - по гіпербол (EN і DM).
Поверхні, що задаються каркасом.
До них відносяться поверхні, утворення яких не підпорядковане певним геометричному закону. Ці поверхні задають каркасом - сімейством ліній, що належать їм і паралельних координатним площинам (рис. 10).
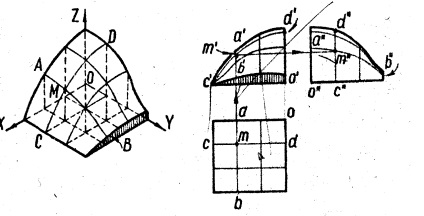
На рис. 10 зображений об'ємний графік, який використовується в радіотехніці. Поверхня визначена кривими лініями, одне сімейство яких (CD) паралельно площині XOZ, а інше (АВ) - площині YOZ. Точка М поверхні визначена як точка перетину кривих АВ і CD.
У радіоелектроніки та автоматики зустрічаються поверхні другого порядку загального виду: еліптичні конус і циліндр, параболічний і гіперболічний циліндри і так далі.
Список використаної літератури.
Анісімов І. К. Конспекти лекцій з нарисної геометрії. - Р. 1970. Наступні
Фролов С. А. Нарисна геометрія: підручник для вузів. - М. Машинобудування, 1983.