II. Перетин кривих поверхонь
Загальні відомості про поверхні
Загальний спосіб побудови лінії перетину однієї поверхні другою
Деякі особливі випадки перетину однієї поверхні другою
Список використаної літератури
Ми знаємо, що фігурою перетину двох прямих є точка, також ми знаємо, що фігурою перетину двох площин є пряма. Криві поверхні теж перетинаються. І тому мета нашої роботи - дізнатися фігуру перетину кривих поверхонь.
Дана тема є актуальною, оскільки завжди існує інтерес до завдань на побудову. У шкільному ж курсі геометрії не розглядаються криві поверхні і випадки їх перетину.
Предметом нашого дослідження є фігури перетину кривих поверхонь, а об'єктом нашого дослідження є самі криві поверхні.
У роботі використані наступні методи:
· Робота з науковою літературою
· Робота зі спеціальною літературою
Загальні відомості про поверхні
Поверхня - це геометричне місце лінії, що рухається в просторі за певним законом. Цю лінію називають що утворює. Вона може бути прямою, тоді утворену їй поверхню відносять до класу лінійчатих. Якщо утворює - крива лінія, поверхня вважають нелінійчатих. Лінію, по якій переміщують утворить, називають направляючої. В якості останньої іноді використовують слід поверхні.
Визначником поверхні називають сукупність умов, які задають поверхню в просторі.
Поверхня вважають заданою, якщо можна побудувати проекції будь-якої її утворює. Одну і ту ж поверхню можна утворити рухом різних ліній. Наприклад, сфера утворюється обертанням кола навколо її діаметра.
Розглянуті нижче поверхні класифіковані в такий спосіб.
I. Поверхні обертання лінійчатих.
3. Однопорожнинний гіперболоїд.
II. Поверхні обертання нелінійчатих.
2. Тор (кругової, параболічний, еліптичний).
3. Еліпсоїд (витягнутий і стиснутий).
4. Поверхня обертання загального виду.
Поверхні обертання лінійчатих.
Всі поверхні цього класу утворені обертанням прямої лінії навколо іншої прямої. Дві прямі можуть займати відносно один одного три різних положення. Кожному з них відповідає своя поверхню обертання.
1. Конус утворюють обертанням прямий ODвокруг пересічної з нею осі Z (рис. 2, а). Координатні площини XOZі YOZрассекают конус по пересічним прямим OD, OE, OK і OF; площину XOZ дає в перетині точку О; площину. паралельна XOY, перетинає по колу (DFEK).
Для побудови точки, що належить кривій поверхні, її поверхні маємо на проекціях лінії, що лежить на цій поверхні.
Конус бере участь в утворенні форми діаграми спрямованості антени, поверхні положення об'єкта в просторі, антени і її опромінювача, дифузора гучномовця, резонатора, відбивача радіохвиль, електронно-променевих трубок і електронних ламп, світловода, деталей вакуумних установок і так далі.
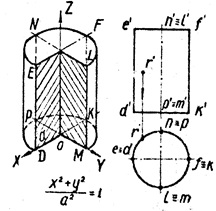
2. Циліндр утворюють обертанням прямий ЕD навколо паралельної їй осі Z (рис. 2, б, в)
Площині XOZі YOZ перетинають його вздовж паралельних прямих ED, FK, NP, LM, а площину XOY і їй паралельні - по колах DPKM і (ENFL).
Циліндр застосовують при утворенні форми хвилеводів, антен, амортизаторів приладів, дзеркал лазерів, корпусів датчиків і так далі.
Поверхні обертання нелінійчатих.
До цього класу відносять в основному поверхні, утворені обертанням кривих другого порядку.
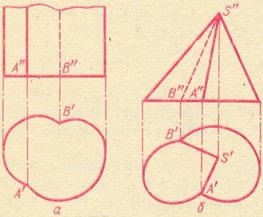
1. Сферу утворюють обертанням окружності навколо її діаметра (рис. 4). Будь-яка площина перетинає сферу по колу. Нарис фронтальної проекції сфери називають головним меридіаном, нарис горизонтальної проекції - екватором. Проекції точки К, що лежить на поверхні сфери, належать проекція горизонтальної окружності, проведеної на сфері.
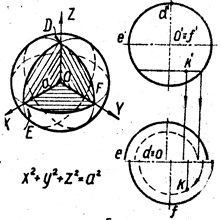
Сфера утворює форму діаграми спрямованості антен, обтічника і випромінювача антени, головки мікрофона, контактів реле і так далі. Сфера є поверхнею положення об'єкта в просторі.
2. Круговий тор утворюють обертанням окружності навколо осі, що лежить в площині цієї окружності і що є її діаметром. Таким чином, сферу можна розглядати як окремий випадок тора. Розрізняють тор-кільце, коли вісь обертання не перетинає утворить коло, і тор-бочку.
У радіотехніці використовують також параболічний і еліптичний тор.
Параболічний тор утворюють обертанням параболи навколо прямої, що лежить в площині цієї параболи і що є її фокальній віссю.
Еліптичний тор утворюють обертанням еліпса навколо прямої, що лежить в площині цього еліпса і не є його віссю.
Торовиє поверхні мають діаграми спрямованості антен, поверхні положення об'єкта в просторі, антени і їх обтічники, хвилеводи, резонатори, гучномовці і так далі.
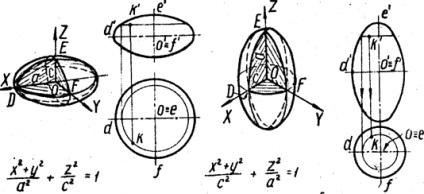
3. Еліпсоїд утворюють обертанням еліпса навколо його малої або великої осі. У першому випадку отримують стиснений (рис. 5, а), а в другому - витягнутий еліпсоїди обертання (рис. 5, б).
Площині XOZ і YOZ перетинають їх по еліпсам DE і EF, а площину XOY - по колу DF.
Форму еліпсоїда мають дзеркала антен і лазерів, випромінювачі антен, поверхні положення і так далі.
4. Поверхня обертання загального виду утворюють обертанням довільної кривої.
ЗАГАЛЬНИЙ СПОСІБ ПОБУДОВИ ЛІНІЇ ПЕРЕТИНУ ОДНІЄЇ поверхні іншої
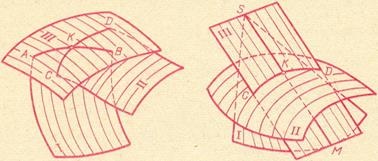
Загальним способом побудови лінії перетину однієї поверхні другою є знаходження точок цієї лінії за допомогою деяких січних поверхонь (для ліній перетину застосовується також назву «лінії переходу», особливо в тих випадках, коли при переході від однієї поверхні до іншої немає яскраво вираженого перетину. Для допоміжних січних поверхонь зустрічається назва «посередники»). На малюнку 1 зліва показано, що поверхні I і II пересічені деякої поверхнею III; ця допоміжна поверхня перетинає поверхню I по лінії АВ, а поверхню II - по лінії CD. Точка К, в якій перетинаються лінії АВ і CD, загальна для поверхонь I і II, отже, належить лінії їх перетину. Повторюючи такий прийом, отримуємо ряд точок шуканої лінії.
Застосовуючи зазначений загальний спосіб для побудови лінії перетину двох кривих поверхонь, ми можемо:
1) перетинати поверхні допоміжними площинами;
2) перетинати поверхні допоміжними кривими поверхнями (наприклад, сферами).
У деяких випадках при вирішенні задач комбінують застосування допоміжних площин і кривих поверхонь. Слід по можливості підбирати такі допоміжні поверхні, які в перетині з даними поверхнями дають прості для побудови лінії (наприклад, прямі або кола).
У загальному випадку допоміжні січні площини застосовують і для побудови лінії перетину кривої поверхні гранной.
Викладений загальний спосіб побудови лінії перетину однієї поверхні другою не виключає застосування іншого способу, якщо хоча б одна з цих поверхонь лінійчата: знайти точку, в якій прямолінійна твірна однієї поверхні перетинає іншу поверхню, і, повторюючи цей прийом для ряду утворюють, через знайдені точки провести шукану лінію. На малюнку 1 справа показано, що через творчу SM поверхні I проведена площину III, яка перетинає другу поверхню (II) по кривій CD; утворює SM перетинає цю криву в точці К, через яку пройде шукана лінія перетину поверхонь I і II.
Це відноситься і до випадку перетину кривої поверхні гранной: тут роль утворюють грають ребра гранной поверхні.
Отже, для побудови точок лінії, що виходить на одній поверхні при перетині її іншою поверхнею, користуються допоміжними січними площинами приватного і загального стану, кривими поверхнями, прямолінійними утворюючими кривих лінійчатих поверхонь і ребрами гранних поверхонь. При цьому вдаються до способів перетворення креслення, якщо це спрощує і уточнює побудову.
При побудові точок лінії перетину спочатку слід знайти ті точки, які зазвичай називають характерними (для них також застосовується назва «опорні»). Це точки, проекції яких відокремлюють видиму частину проекції лінії перетину від невидимої, це проекції точок лінії перетину, найвищих та найнижчою по відношенню до площини π1, найближчих і найбільш віддалених по відношенню до глядача, крайніх зліва і справа на проекціях лінії перетину.
ДЕЯКІ ОСОБЛИВІ ВИПАДКИ ПЕРЕТИНУ ОДНІЄЇ поверхні іншої
1. На малюнку 2 зображені пересічні між собою: а) два циліндра з паралельними утворюючими, б) два конуса із загальною вершиною. В обох випадках лініями перетину поверхонь є загальні утворюють цих поверхонь.
Покладемо, що треба побудувати проекції прямої, що проходить через точку В на осі проекцій і розташованої під кутом # 966; 1 по відношенню до площини π1 і під кутом # 966; 2 до площини π 2. Відомо, що для прямої загального положення # 966; 1 + # 966; 2<90градусов.
Геометричним місцем прямих, що проходять через дану точку і складових з площиною π1 кут # 966; 1, є конічна поверхня обертання, вершина якої знаходиться в даній точці, а утворюють складають з площиною π1 кут # 966; 1.
Точно також геометричним місцем прямих, що проходять через дану точку і складових з площиною π2 кут # 966; 2, є конічна поверхня обертання, вершина якої знаходиться в даній точці, а утворюють складають з площиною π2 кут # 966; 2.
Очевидно, шукана пряма повинна одночасно належати поверхнях обох конусів, що мають спільну вершину в даній точці, тобто повинна бути лінією їх перетину - загальної їх утворює. Ми отримаємо вісім променів, що виходять з точки В, що відповідають поставленим умовам (чотири прямих).
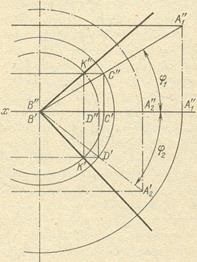
На малюнку 3 виконано побудову одного з цих променів. Перший конус визначається утворює Ва1 і віссю, перпендикулярної до площини π1, а другий конус - утворює Ва2 і віссю, перпендикулярної до площини π2. Для побудови шуканої прямої є поки лише точка В - загальна вершина конусів. Другу точку - точку К - загальну для поверхонь цих конусів, ми знаходимо за допомогою сфери з центром в точці В.
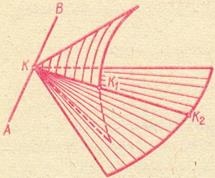
Іншим прикладом, коли в процесі деякого побудови використовується властивість перетину двох конічних поверхонь із загальною вершиною по загальній для них прямої лінії - утворює, служить побудова утворюють лінійчатої поверхні, званої циліндром з трьома напрямними. Покладемо (рис.4), що в числі напрямних одна пряма АВ і дві криві лінії. Якщо взяти точку (К) на прямій направляючої і прийняти її в якості загальної вершини допоміжних конічних поверхонь, для яких дані криві служать напрямними, то пряма перетину цих конічних поверхонь, проходячи через їх вершину, перетне і їх направляючі, тобто виявиться прямолінійною твірною циліндра з трьома напрямними. Очевидно, треба взяти ряд точок заданої прямої і виконати для кожної з них вказане побудова, що дасть ряд утворюють циліндра з трьома напрямними.
Якщо для цієї поверхні все три напрямні криві, то зазначений спосіб побудови залишається таким же: точки, службовці вершинами для допоміжних конічних поверхонь, беруться на одній з даних кривих.
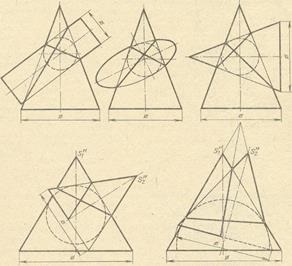
2. При взаємному перетині поверхонь обертання другого порядку виходить в деяких випадках розпаду лінії перетину на дві плоскі криві другого порядку. Це буває в тих випадках, коли обидві пересічні поверхні обертання (циліндр і конус, два конуса, еліпсоїд і конус і т. П.) Описані навколо спільної для них сфери. У прикладах, наведених на рис. 5, в перших трьох випадках перетину відбувається по еліпсам, в четвертому - по еліпсу і параболі, а в п'ятому - по еліпсу і гіперболи.
На рис. 6 показані два циліндра рівного діаметру з пересічними осями. З точки перетину осей може бути проведена сфера, вписана в обидва циліндра. Обидві поверхні перетинаються по лінії, що складається з двох еліпсів. На рис. 6 праворуч також зображені два циліндра рівного діаметра, але їх осі перетинаються на цей раз не під прямим кутом. Лінія перетину складена з половин двох еліпсів.
Зображені на рис. 5 і 6 криві перетину поверхонь проектуються на фронтальну площину проекцій у вигляді прямолінійних відрізків, так як загальна площина симетрії для кожної пари розглянутих поверхонь розташована паралельно площині π2.
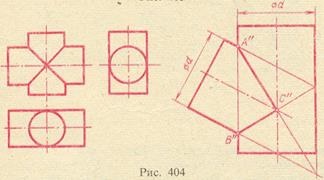
У розглянутих прикладах має місце подвійне зіткнення двох пересічних поверхонь другого порядку, тобто наявність у цих поверхонь двох точок дотику, а отже, і двох площин, кожна з яких стосується обох поверхонь в загальній їх точці. Наведемо без доказів наступні два положення, на яких засновані зазначені вище побудови: 1) поверхні другого порядку, які мають подвійне зіткнення, перетинаються між собою за двома кривими другого порядку, причому площині цих кривих проходять через пряму, яка визначається точками дотику; 2) дві поверхні другого порядку, описані навколо третьої поверхні другого порядку (або в неї вписані (наприклад, два стислих еліпсоїда обертання, вписаних в сферичну поверхню)), перетинаються між собою за двома кривими другого порядку. Друге положення, відоме під назвою теореми Монжа, випливає з першого.
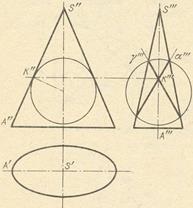
На підставі викладеного можна знайти кругові перетину еліптичного конуса і еліптичного циліндра. Приклад дан на мал. 7. Взято деяка сфера так, щоб вона мала подвійне зіткнення з поверхнею еліптичного конуса. У перетині сфери з конусом виходять дві плоскі криві - окружності в профільно-прецірующіх площинах # 947; і # 945 ;, дають дві системи кругових перерізів еліптичного конуса.
3. співвісний поверхні обертання (т. Е. Поверхні із загальною віссю) перетинаються по колах. На рис. 8 дано три приклади: а) циліндр і конус, б) стислий еліпсоїд і усічений конус, в) дві сфери. У всіх цих прикладах дані лише фронтальні проекції, причому загальна вісь поверхонь розташована паралельно площині π2. Тому окружності, одержувані при перетині однієї поверхні другою, проектуються на π2 у вигляді прямолінійних відрізків.
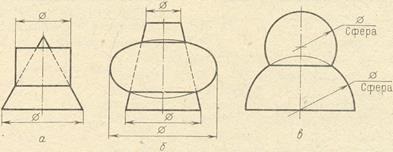
За вісь сфери можна прийняти будь-який її діаметр. Тому пересічні сфери розглядаються як співвісні поверхні обертання. Також в якості співвісних поверхонь можуть бути розглянуті зображені на рис. 9 циліндр і сфера, конус і сфера, деяка поверхню обертання і сфера. Осі циліндра, конуса і поверхні обертання проходять через центри сфер. Перетин відбувається по колах.
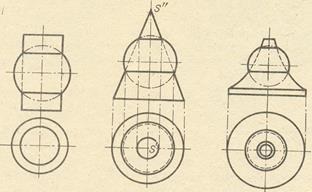
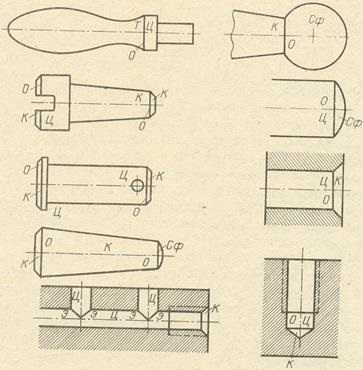
На рис. 10 наведено приклади зображення співвісних поверхонь обертання і зустрічних сверлений одного і того ж діаметру з практики машинобудівного креслення. Поверхні позначені буквами: Т - круговий кільце, К - конус, Ц - циліндр, Сф - сфера; отримані в перетині лінії позначені буквами: О - окружність, Е - еліпс. Ці лінії проектуються у вигляді прямолінійних відрізків, тук Кук осі поверхонь паралельні площині проекцій (в даному випадку площині π2).
В результаті нашого дослідження ми:
· Розширили свої уявлення про взаємне розташування поверхонь в просторі
· Вивчили можливі фігури перетину поверхонь в просторі
· Чи навчилися будувати лінії перетину кривих поверхонь
Я вважаю, що дана робота корисна учням, які цікавляться математикою, і може бути використана на факультативних заняттях з геометрії.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Анісімов І. К. Конспекти лекцій з нарисної геометрії. - Р. 1970. Наступні
2. Гільберт. Д. Наочна геометрія. - М. Наука, 1981.
3. Гордон В.О. Курс нарисної геометрії. - М. Наука, 1988.
4. Фролов С. А. Нарисна геометрія: підручник для вузів. - М. Машинобудування, 1983.
Дякую за допомогу! Зроби паузу, студент, ось розважся: Препод на іспиті: От раніше, в молодості, я лютував - закидав студентів тільки так, а зараз постарів, подобрішав. візьміть заліковку, прийдете на перездачу. До речі, анекдот узятий з chatanekdotov.ru