Реалізація звичайного алгоритму Флойда-Уоршелла потрібна мені для того, щоб запрограмувати паралельне обчислення цього завдання за допомогою бібліотеки MPI. Звіт про результати розпаралелювання я напишу вже зовсім скоро (я дуже на це сподіваюся). А зараз поговоримо про стандартний алгоритмі Флойда-Уоршелла.
Суть алгоритму Флойда-Уоршелла
Як я згадав, алгоритм призначений для знаходження найкоротших шляхів між усіма вершинами в графі. По суті він являє собою простий перебір всіх шляхів і вибір з них найменшого. Перебір здійснюється по так званій «матриці суміжності» розміру NxN, де N - кількість вершин графа.
На перетині i-го рядка і j-го стовпця матриці стоїть значення ваги ребра з вершини i в вершину j. Головна діагональ матриці суміжності це завжди нулі, тому що ребер з i-ї вершини в i-ую в графі бути не повинно. У тому випадку, коли між вершинами немає ребра, в матриці буде стояти умовна нескінченність (INF).
Реалізація алгоритму Флойда-Уоршелла
Реалізується пошук найменшого відстані послідовним перебором всіх шляхів. У три цикли, зовнішній вибирає вершину, через яку ми пробуємо знайти кращий шлях. Внутрішні два перебирають пари вершин, між якими ми шукаємо мінімальну відстань.
Матрицю суміжності найзручніше зберігати в файлі в наступному вигляді: першим рядком кількість вершин, потім безпосередньо сама матриця. Як нескінченно велику відстань (INF, коли вершини не пов'язані ребром) взяти конкретну константу. У моїй реалізації вона дорівнює 101, це означає, що максимальна вага ребра не може бути більше 100.
Приклад файлу з матрицею
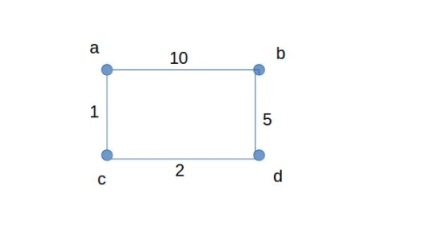
Вихідний код алгоритму
Приклад роботи з алгоритмом
висновок
Звичайний алгоритм Флойда-Уоршелла реалізується дуже просто, але працює дуже довго на великих матрицях. Ідеальний кандидат для того, щоб віддати його на розтерзання бібліотеці MPI. На сьогодні у мене все, спасибі за увагу!