Будує ЗD-rpaфікі типу труби.
Серед цих функцій треба відзначити насамперед кошти побудови графіків ряду нових типів (наприклад, у вигляді ліній рівного рівня, векторних полів і т.д.), а також кошти об'єднання різних графіків в один. Особливий інтерес представляють дві перші функції, що забезпечують пожвавлення (анімацію) як двовимірних графіків (animate), так і тривимірних (animate3d). Цей пакет цілком
заслуговує опису в окремій книзі. Але, з огляду на обмежений обсяг даної книги, ми розглянемо лише кілька характерних прикладів його застосування. Зауважимо, що для використання наведених функцій потрібен виклик пакета, наприклад, командою with (plots).
13.6.2. Побудова графіків функцій в двовимірної полярній системі координат
У пакеті plots є функція для побудови графіків в полярній системі координат. Вона має вигляд polarplot (L, o), де L - об'єкти для завдання функції, графік якої будується і про - необов'язкові опції. На рис. 13.27 представлений приклад побудови графіка за допомогою функції polarplot.
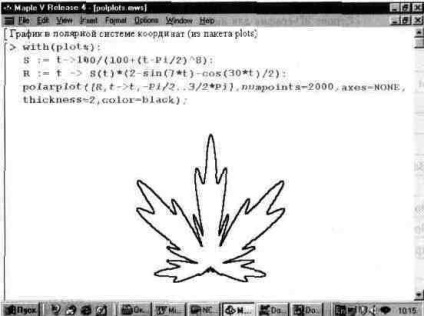
Мал. 13.27. Графік, побудований за допомогою функції polarplot.
В даному випадку для більшої виразності опущено побудова координатних осей, а графік виведений лінією подвоєною товщини. Графік дуже нагадує лист клена, вельми шанованого в Канаді і став емблемою системи Maple V.
13.6.3. Побудова графіків лініями рівного рівня
Графіки, побудовані за допомогою ліній рівного рівня (їх також називають контурними графіками) часто використовуються в картографії. Ці графіки виходять, якщо подумки провести через тривимірну поверхню ряд рівновіддалених площин, паралельних площині, утвореної осями Х і Y графіка. Лінії рівних висот утворюються в результаті перетину цих площин з тривимірною поверхнею.
Для побудови таких графіків використовується функція contourplot, яка може використовуватися в декількох форматах:
contourplot ([exprf, exprg, exprh], s = a..b, t = c..d)
contourplot ([f, g, h], a..b, c..d)
contourplot3d ([exprf, exprg, exprh], s = a..b, t = c..d) » '
contourplot3d ([f, g, h], a..b, c..d)
Тут - f, g і h - функції, expri - вираз, що описує залежність висоти поверхні від координат х і у, exprf, exprg і exprh - вираження, що залежать від s і t, що описують поверхню в параметричної формі, а й b - константи речового типу, end - константи або вирази дійсного типу, х, y ,, s і t - імена незалежних змінних.
На рис. 13.28 показано побудову графіка лініями рівного рівня для однієї функції. Опція filled = true забезпечує автоматичну функціональну забарвлення замкнутих фігур, утворених лініями рівного рівня. Часом це додає графіку більшої виразності, ніж при побудові тільки ліній рівного рівня.
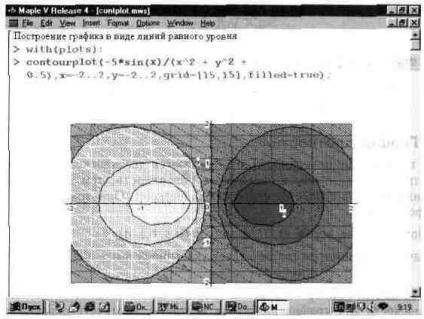
Мал. 13.28. Приклад побудови графіка функції лініями рівного рівня.
Функція contourplot дозволяє будувати і графіки ряду функцій. Приклад такої побудови показаний на рис. 13.29. Безліч кіл на цьому малюнку створюється чотирма поверхнями, заданими функціями с1, с2, СЗ і с4.
Слід зазначити, що, хоча графіки у вигляді ліній рівного рівня виглядають не так естетично і природно, як звичайні графіки тривимірних поверхонь (бо вимагають осмислення результатів), у них є один істотний плюс - екстремуми функцій на таких графіках виявляються часом більш чітко, ніж на звичайних графіках. Наприклад, невелика височина або западина за великий «горою» на звичайному графіку може виявитися невидимою, оскільки затуляється
«Горою» - на графіку ліній рівного рівня цього ефекту немає. Однак виразність таких графіків сильно залежить від числа ліній рівного рівня.
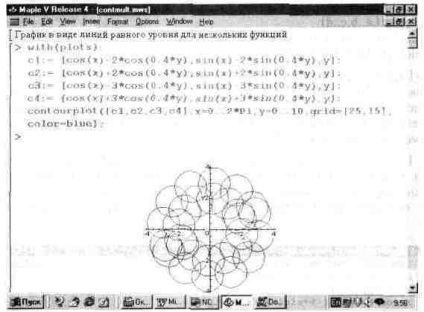
Мал. 13.29. Приклад побудови графіків багатьох функцій лініями рівного рівня.
13.6.4. Графік щільності
Іноді тривимірні поверхні відображаються на площині як графіки щільності забарвлення - чим вище висота поверхні, тим щільніше забарвлення. Такий вид графіків створюється функцією densityplot. Вона може записуватися в двох форматах:
де призначення параметрів відповідає зазначеному вище для функції contour-plot.
На рис. 13.30 дан приклад побудови графіка такого типу. Неважко помітити, що в площині X, Y графік розбитий на квадрати, щільність забарвлення яких різна. У нашому випадку щільність забарвлення задається відтінками сірого кольору.
Зазвичай графіки такого типу не дуже виразні, але мають свої області застосування. Наприклад, відтінки забарвлення напівпрозорої рідини можуть вказувати на рельєф поверхні дна ємності, в якій знаходиться ця рідина.
13.6.5. Графік векторного поля двовимірний
Ще один поширений спосіб представлення тривимірних поверхонь - графіки векторного поля. Вони часто застосовуються для відображення полів, наприклад, електричних зарядів. Особливість таких графіків в тому, що для їх побудови використовують стрілки, напрям яких відповідає напрямку зміни градієнта поля, а довжина - значенням градієнта.
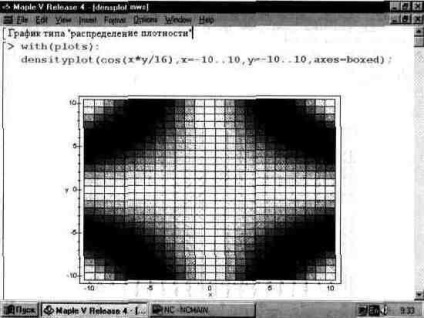
Мал. 13.30. Графік щільності для заданої функції.
Для побудови таких графіків в двовимірної системі координат використовується функція fieldplot:
fieldplot (f, rl, r2) або fieldplot (f, rl, r2.),
де f - вектор або безліч векторів, які задають побудова, і rl і r2 - межі.
На рис. 13.31 показаний вид одного з таких графіків. Слід зазначити, що для отримання достатнього числа чітко видних стрілок треба попрацювати з форматуванням графіків. Інакше графіки цього типу можуть виявитися не дуже представницькими. Так, занадто короткі стрілки перетворюються в рисочки і навіть точки, що не мають вістря, що позбавляє графіки наочності.
Трохи пізніше ми розглянемо побудову на одному малюнку графіків щільності і векторного поля, а також створення більш наочних жирних стрілок.
13.6.6. Графіки в різних системах координат
У пакеті plots є безліч функцій для побудови графіків в різних системах координат. Обсяг книги не дозволяє відтворити приклади на всі види таких графіків, бо їх багато сотень. Та це й не треба - у вбудованих в довідкову систему прикладах можна знайти всі необхідні відомості. Так що обмежимося лише парою прикладів застосування функції tubeplot (C, options), що дозволяє будувати досить наочні фігури в просторі, що нагадують труби або інші об'єкти, утворені фігурами обертання.
На рис. 13.32 показана одна з таких фігур. Вона разюче нагадує раковину равлика. Функціональна забарвлення досягнута доопрацюванням графіка за допомогою панелі форматування. Сенс параметра С (в документі Conchoid) легко зрозуміти з цього прикладу.
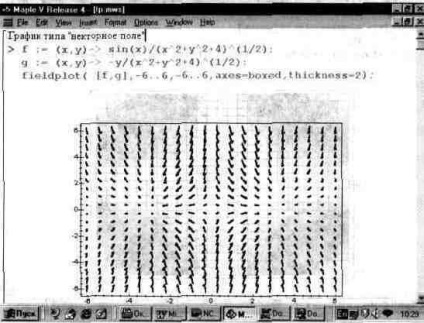
Мал. 13.31. Двовимірний графік типу векторного поля.
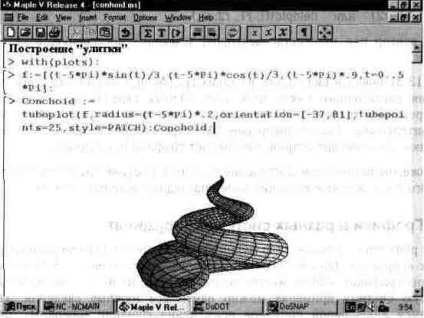
Мал. 13.32. Побудова графіка «равлики».
Ця функція може використовуватися і для побудови ряду трубчастих об'єктів в просторі. При цьому автоматично задається алгоритм видалення невидимих ліній навіть для досить складних фігур. Це наочно ілюструє приклад
на рис. 13.33, що показує фігуру «ланцюга». Чи не правда реалістичність цієї фігури вражає уяву?
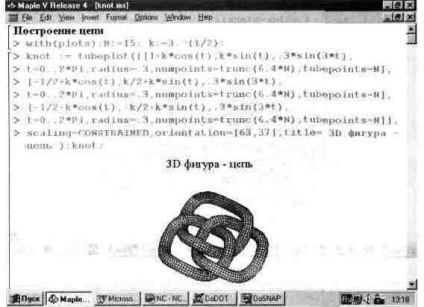
Мал. 13.33. Фігура «ланцюга», побудована із застосуванням функції tubeplot.
Можна чимало міркувати про те, як природа «дізналася» про математичних закономірностях, покладених в основу тих чи інших геометричних об'єктів, або, можливо, про геніальність людей, які зуміли знайти такі закономірності для природних об'єктів. У наш час Maple V відкриває величезні можливості для таких людей.
13.6.7. Графіки типу тривимірного векторного поля
Наочність ряду графіків можна істотно збільшити, будуючи їх у тривимірному поданні. Наприклад, для такого побудови векторних полів можна використовувати графічну функцію fieldplot3d. На відміну від функції fieldplot, вона будує стрілки як би в тривимірному просторі (рис. 13.34).
Все сказане про особливості таких двовимірних графіків залишається справедливим і для графіків тривимірних. Зокрема, для отримання достатньої їх показності потрібно ретельно налагоджувати формати представлення таких графіків.
13.6.8. Контурні тривимірні графіки
На відміну від векторних графіків, контурні графіки тривимірних поверхонь, накладені на самі ці поверхні, нерідко підвищують сприйнятливість таких поверхонь - подібно зображенню ліній каркаса. Для одночасного побудови тривимірної поверхні і контурних ліній на них служить функція contourplot3d. Приклад її застосування показаний на рис. 13.35.

Мал. 13,34. Побудова векторного поля в тривимірному просторі.
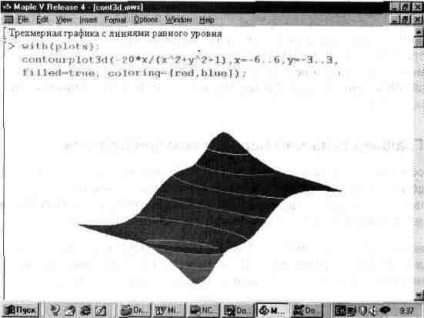
Мал. 13.35. Графік тривимірної поверхні з контурними лініями.
Для підвищення наочності цей графік доопрацьований за допомогою панелі форматування графіків. Зокрема, включена функціональна забарвлення і підібрані кути огляду фігури, при яких чітко видно западина і пік фігури.
13.6.9. Техніка візуалізації складних просторових фігур
Наведені вище досить прості приклади дають уявлення про високий ступінь візуалізації геометричних фігур за допомогою пакета plots. Тут ми розглянемо ще кілька прикладів візуалізації тривимірних фігур. Багато хто бачив котушки індуктивності, у яких провід того чи іншого діаметра намотаний на тороїдальний магнітний сердечник. Математична абстракція такої котушки показана на рис. 13.36.
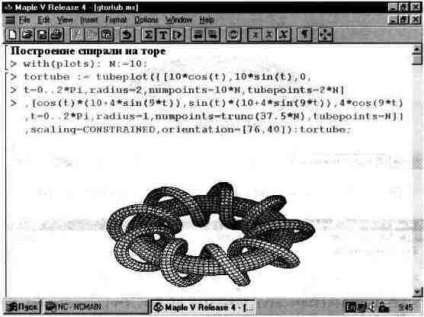
Мал. 13.36. Top з обмоткою - товстої спіраллю.
У документі (рис. 13.36) для функції tubeplot використано досить велике число параметрів-опцій. Не завжди їх дія очевидно. Тому на рис. 13.37 показано побудову трьох взаємно перетинаються торів з різними типами їх побудови. Цей малюнок дає також наочне уявлення про можливості побудови декількох графічних об'єктів (представлених функціями р1, р2 і РЗ) за допомогою функції tubeplot.
У ряді випадків наочно представлені фігури можна будувати із застосуванням об'єднання однотипних фігур. Приклад графіка подібного роду представлений