Розрахунково-графічна робота № 2
Частина 2. Взаємне перетинання тел
Освоїти основні прийоми побудови лінії перетину геометричних тел. Вивчити метод допоміжних площин і метод сфер. Навчитися користуватися ними при вирішенні комплексних завдань.
Для виконання роботи необхідно знати основні положення нарисної геометрії:
-поняття кривої лінії;
-поняття опорних точок;
-сутність способу допоміжних площин;
-сутність методу концентричних сфер і область його застосування;
- сутність методу ексцентричних сфер і область його застосування.
Робота складається з двох завдань, при вирішенні яких необхідно вміти:
-користуватися зазначеними методами;
-вміти знаходити опорні точки, точки видимості;
-знаходити проекції точок що належать поверхні.
Робота виконується на форматі А2. Вихідні дані, рамка, штамп виконати простим олівцем відповідно до державних стандартів ЕСКД. Додаткові побудови виконувати кольоровими олівцями або пастою (синьою, зеленою і т.д.), кінцевий результат побудов виділити червоним кольором.
Всі написи на кресленні виконуються простим олівцем шрифтом №5, індекси - шрифт №3,5.
Вихідні дані до задачі 1 представлені в Додатку А, до задачі 2 - в Додатку Б.
Метод допоміжних січних площин
Метод використовується для визначення проекцій ліній перетину двох геометричних тел: багатогранника і поверхні обертання, двох багатогранників, двох поверхонь обертання.
При вирішенні завдань на взаємне те поверхонь слід пам'ятати такі положення:
1. Щоб знайти точку, що належить лінії перетину необхідно обидва геометричних тіла розсікти допоміжної площиною так, щоб в перерізі площиною утворилися прості фігури - відрізок, окружність, трикутник, прямокутник. Розглядається перетин простих фігур і визначаються загальні точки. Використання декількох допоміжних площин дозволяє визначити ряд точок лінії перетину. З'єднувати можна тільки ті точки, які знаходяться на одній грані багатогранника.
2. Якщо бокова поверхня циліндра або призми займає відносно площини проекцій проецирующее положення (що утворюють поверхні перпендикулярні цій площині проекцій), то одна проекція лінії перетину вже є і вона збігається з проекцією поверхні.
3. Якщо лінія, що належить поверхні, видно не повністю, то точки переходу від видимої частини лінії перетину до невидимої розташовуються на нарисі геометричного тіла. Видима частина лінії перетину повинна бути видимою одночасно для двох геометричних тіл.
4. Щоб знайти верхню чи нижню точку лінії перетину (конуса і багатогранника), що відповідає межі з конусом, потрібно взяти площину, яка повинна проходити через вершину конуса перпендикулярно грані багатогранника (ребрах многогранника).
5. Щоб знайти верхню чи нижню точку лінії перетину (сфера і циліндр), необхідно провести допоміжну площину через осі двох поверхонь.
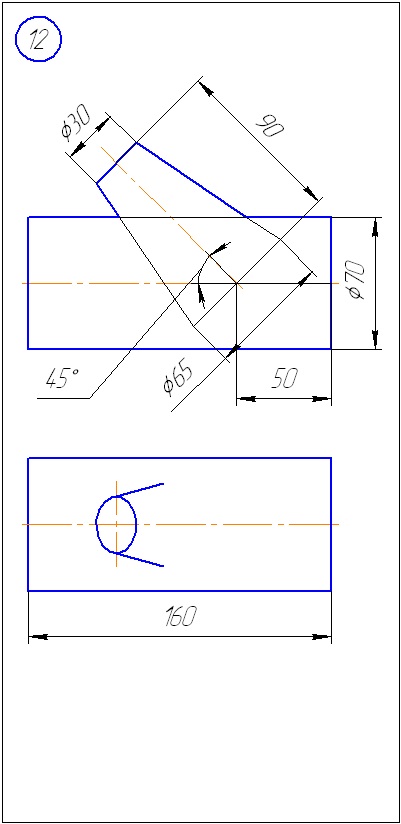
Умова завдання 1:
Побудувати проекції лінії перетину двох геометричних тіл. При вирішенні завдання використовувати метод допоміжних січних площин.
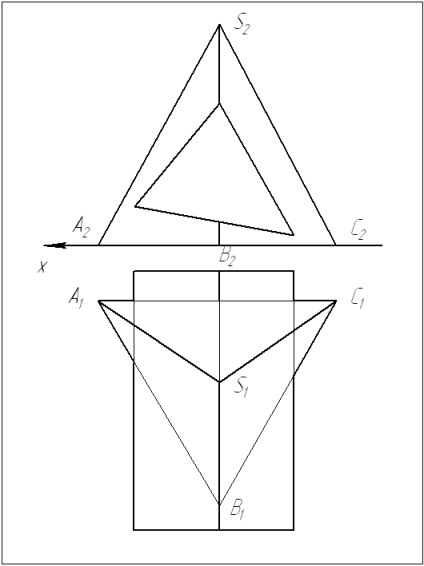
Алгоритм рішення задачі:
1 У цьому завданню утворюють (ребра) призми розташовані перпендикулярно площині проекцій П2. отже, одна готова проекція лінії перетину вже є - на площині П2.
При вирішенні завдання в першу чергу необхідно знайти опорні точки - це вища і нижча точки, або точки, які можна визначити без додаткових побудов. Знаходимо вищу точку 1.
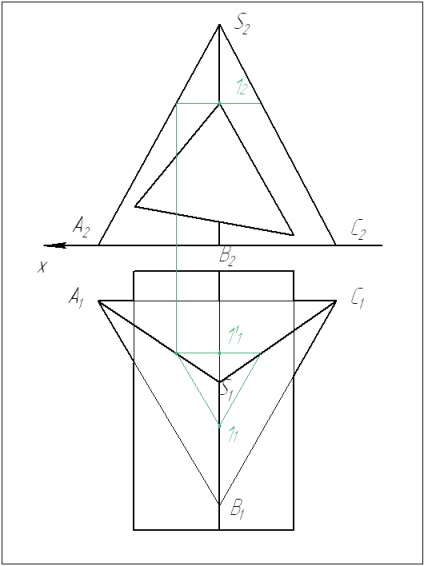
Визначаємо інші опорні точки - 2 і 3.
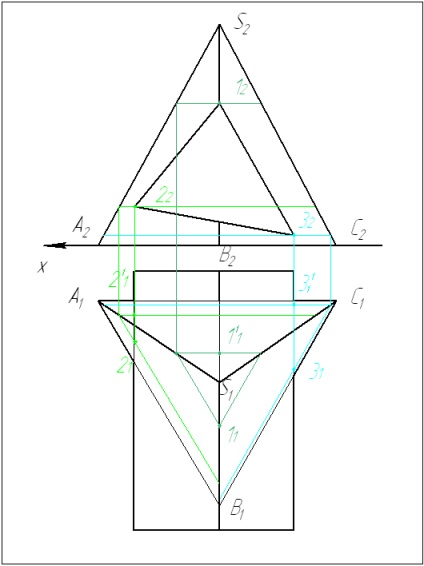
2 Між опорними точками проводимо допоміжну січну площину так, щоб в перерізі утворилися прості фігури: трикутник (для піраміди) і прямокутник (для призми). Перетин цих фігур дає нам шукані точки 4 і 5.
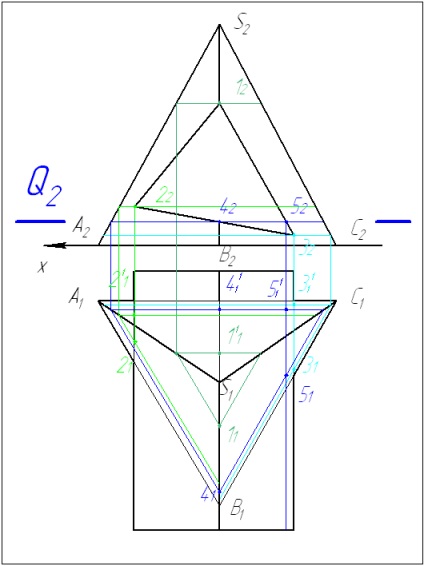
3 У разі, якщо знаходиться лінія перетину поверхонь обертання необхідно проводити кілька допоміжних площин. Для визначення лінії перетину гранних поверхонь досить знайти точки перетину граней з ребрами і отримаємо проекції ламаної лінії перетину.
4 З'єднуємо точки в послідовності, визначеною на фронтальній площині проекцій. Визначаємо видимість отриманої лінії перетину.
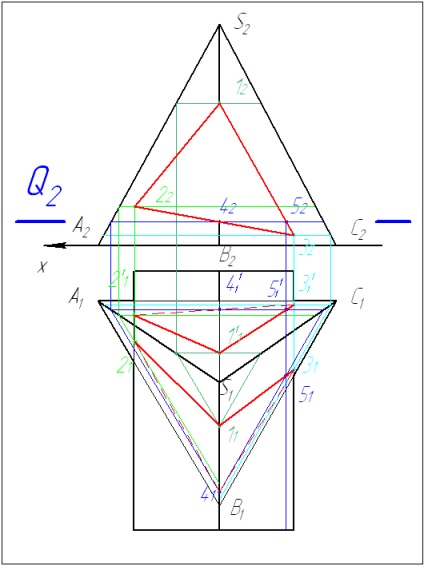
Існують два різновиди методу сфер:
- метод концентричних сфер;
-метод ексцентричних сфер.
Для кожного з цих методів існує ряд обмежень по області застосування. Метод сфер застосуємо, якщо:
- обидва геометричних тіла є поверхнями обертання;
- осі поверхонь лежать в площині, паралельній площині проекцій.
Суть методу сфер полягає в наступному:
На перетині осей поверхонь береться центр сфер. Проводиться сфера довільного радіуса. Сфера перетинає поверхні по колах, які на епюрі вироджуються у відрізки. Розглядаємо перетин відрізків, шукаємо спільні точки. Знайдені точки належатимуть шуканої лінії перетину поверхонь. Проводимо наступну допоміжну сферу, побудови повторюємо, і т.д. Знайдені точки з'єднуємо плавною кривою.
Розглянемо варіанти перетину поверхонь.
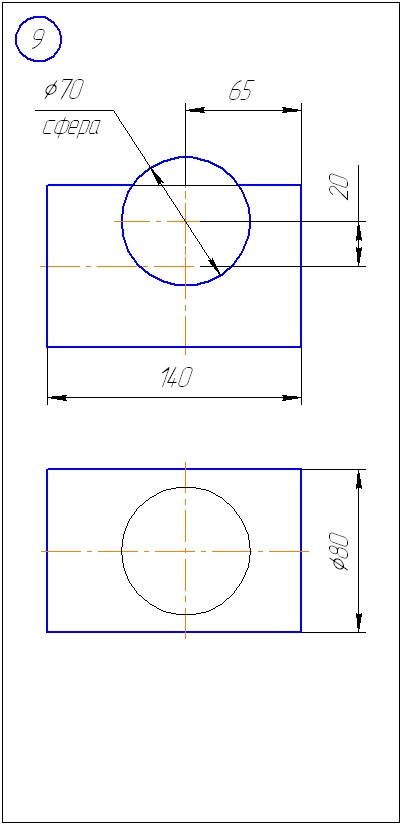
Завдання 1. Побудувати лінію перетину двох поверхонь, одна з яких - сфера. Визначити видимість. Завдання вирішити методом концентричних сфер.
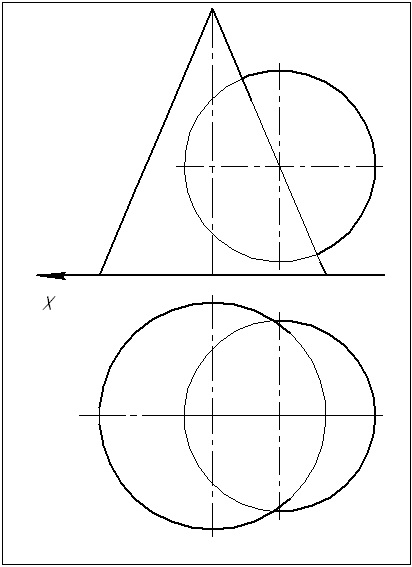
Дану задачу можна віднести до окремого випадку. Таким способом можна вирішувати задачу тільки в разі, якщо одне з тіл - сфера.
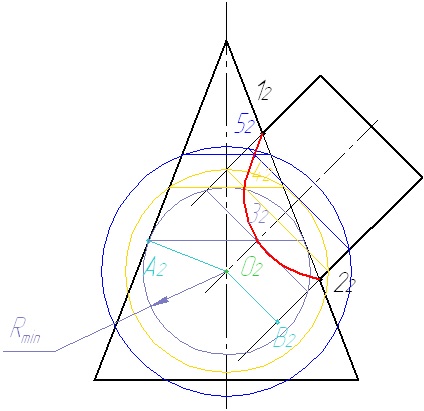
1. Визначаємо опорні точки: вищу 1 і нижчу 2. Знаходимо їх проекції.
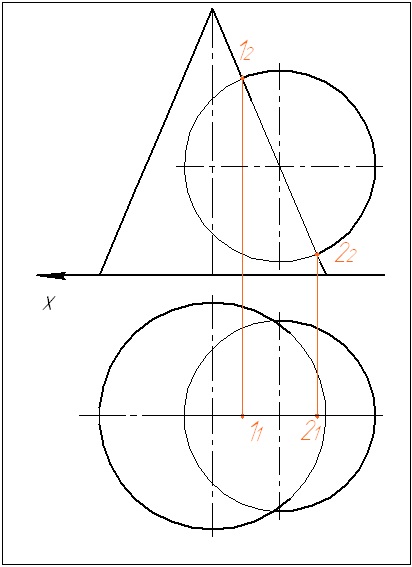
2. На осі конуса довільно вибираємо точку О2 - центр сфер. Визначаємо величину мінімально допустимого радіусу сфери:
.
Визначаємо максимально допустимий радіус сфери:
.
Діапазон значень радіусів сфер:
.

3. Проводимо допоміжну сферу. Визначаємо перетин сфери з поверхнями як точки перетину нарисів поверхонь з дугою. Проводимо відрізки і визначаємо їх точку перетину.
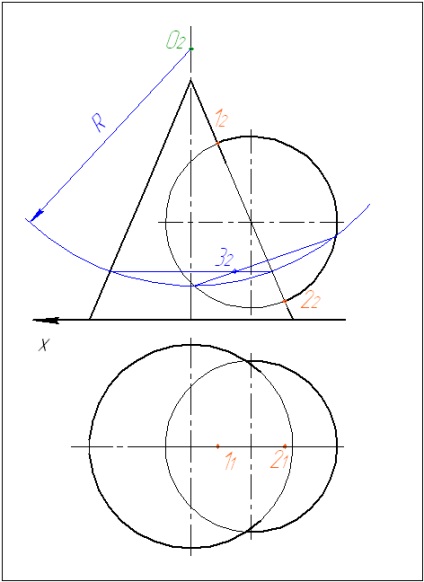
4. Проводимо наступну сферу. Побудови повторюємо.
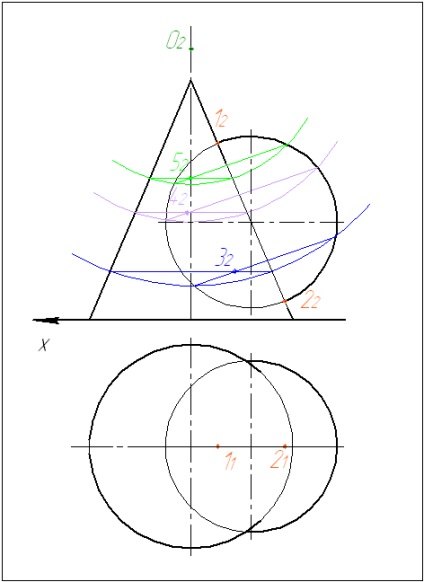
5. З'єднуємо отримані точки плавною кривою.
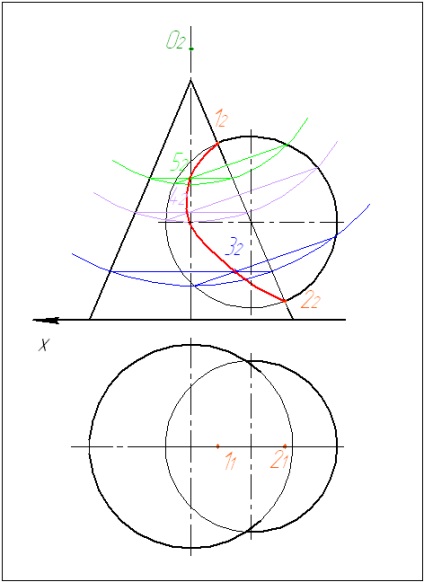
6. Добудовуємо горизонтальну проекцію лінії перетину. Для цього розглядаємо знайдені точки як точки, що належать поверхні конуса. Отримані точки з'єднуємо плавною кривою з урахуванням видимості.
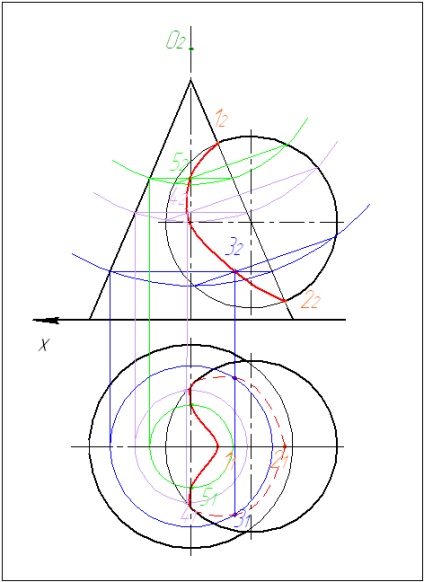
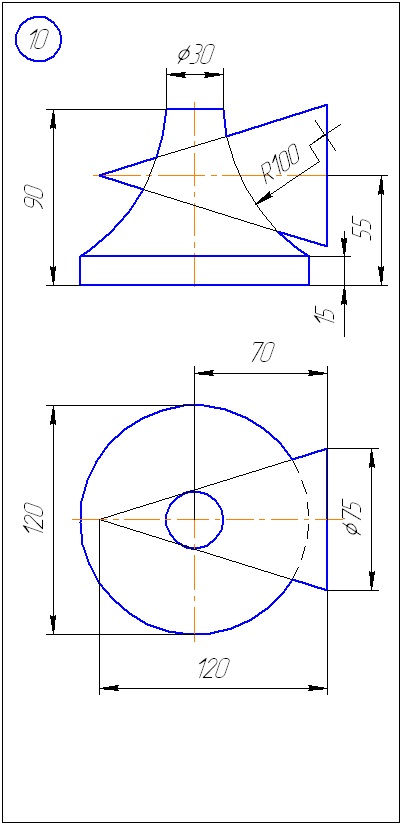
Завдання 2. Побудувати проекції лінії перетину поверхонь. Визначити видимість. Завдання вирішити методом концентричних сфер.
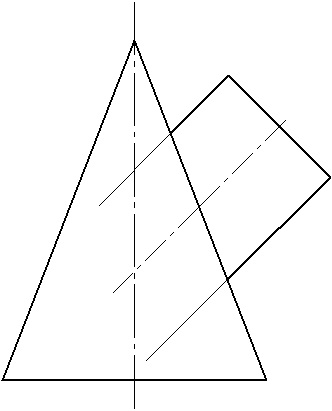
1. Визначаємо опорні точки, як точки перетину нарисів поверхонь.
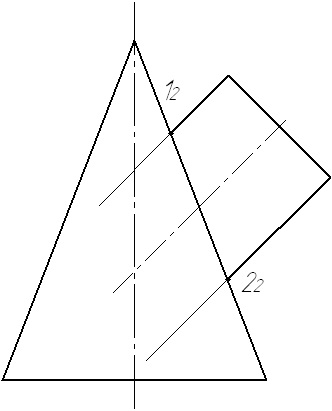
2. Визначаємо центр сфер - як точку перетину осей.
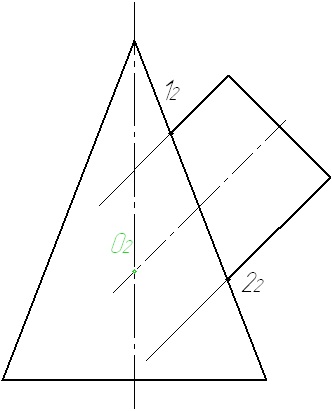
3. Визначаємо максимально можливий радіус сфери
4. Визначаємо мінімально можливий радіус сфери. Для цього з центру сфери проводимо перпендикуляри до створюючих поверхонь.
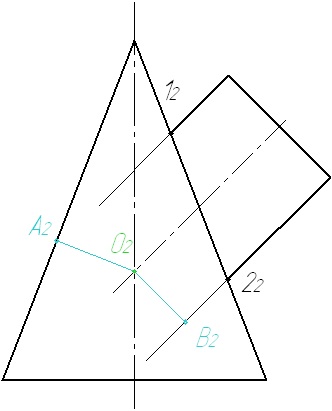
5. Вписуємо сферу мінімального радіуса. Сфера стосується поверхні конуса по колу і перетинає поверхню циліндра по колу. Обидві ці кола на епюрі вироджуються у відрізки. Розглядаємо перетин відрізків, шукаємо спільні точки.
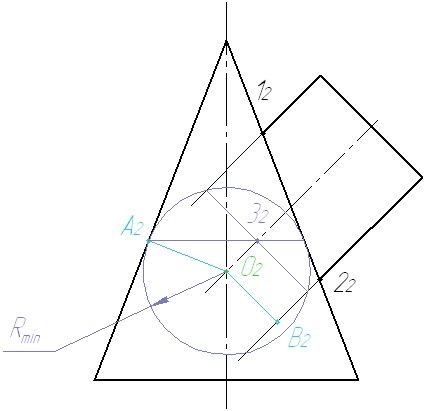
6. Вписуємо сферу довільного радіуса R. Побудови повторюємо.
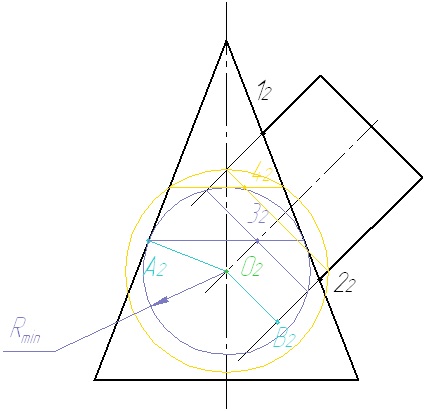
7. Кількість вписаних сфер повинно бути не менше трьох. Отримані таким чином точки, з'єднуємо плавною кривою.
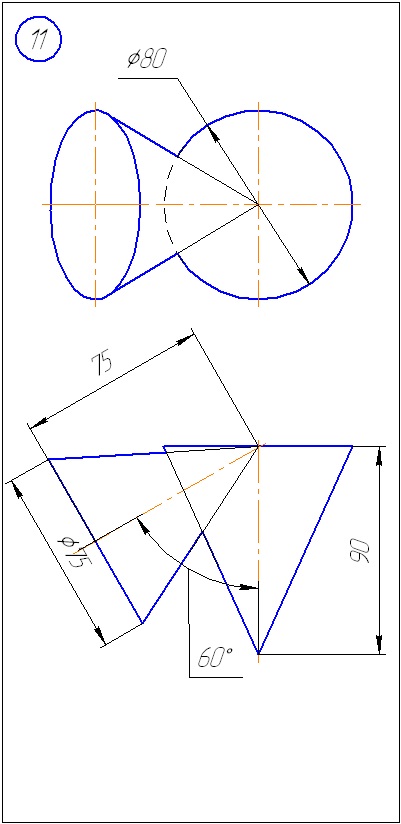
Завдання 3. Побудувати проекції лінії перетину тора з циліндром. Визначити видимість. Завдання вирішити методом ексцентричних сфер.
Метод ексцентричних сфер застосуємо, якщо:
- обидва геометричних тіла поверхні обертання;
- осі поверхонь лежать в площині, паралельній площині проекцій;
- одна з поверхонь - тор.
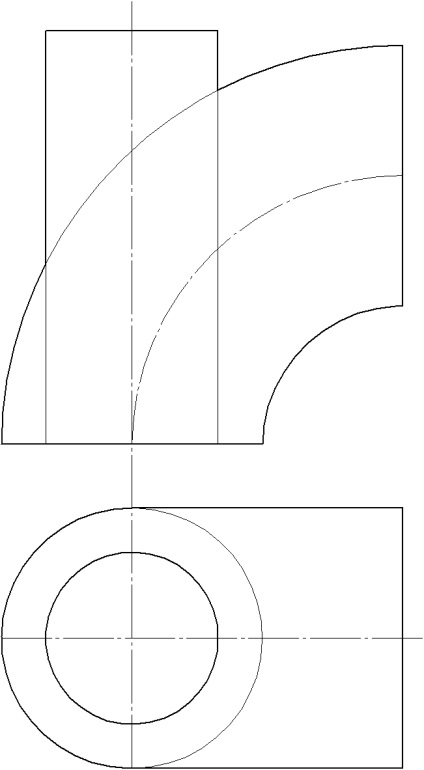
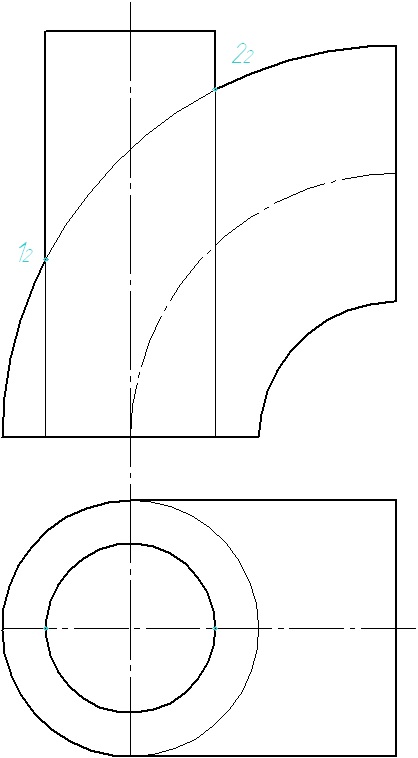
1. Визначаємо опорні точки як точки перетину нарисів.
2. Проводимо проецирующую площину в інтервалі між опорними точками. З точки перетину проецирующей площині з віссю тора відновлюємо перпендикуляр до перетину віссю циліндра. Отримаємо точку О - центр сфер.
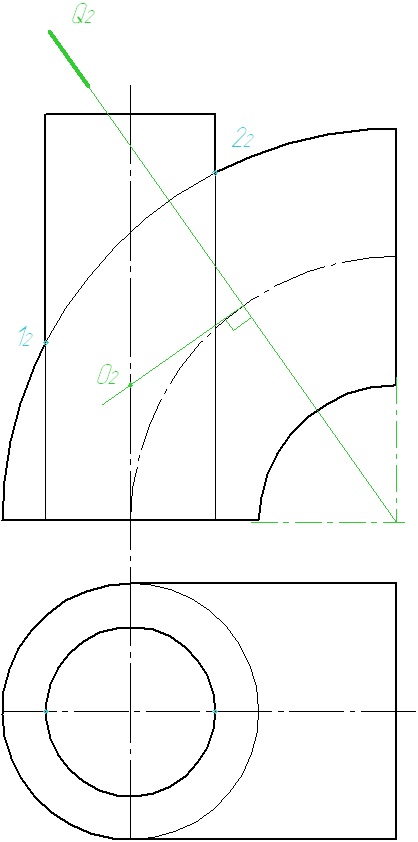
3 З центру О2 проводимо сферу радіуса R. Сфера буде перетинати поверхні циліндра і тора по колах, які на епюрі вироджуються у відрізки. Шукана точка лежить на перетині отриманих відрізків.
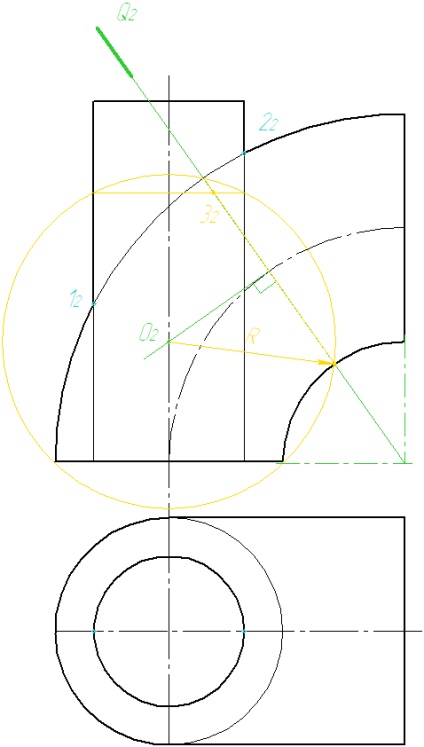
4. Проводимо наступну проецирующую площину. Побудови повторюємо.
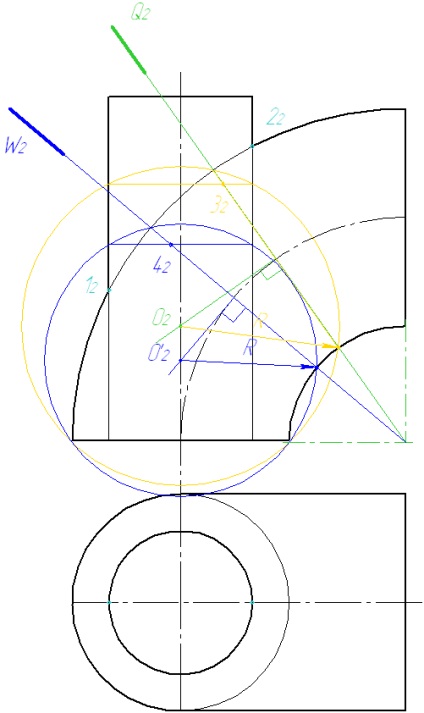
5 Кількість сфер вибирається самостійно, але не менше трьох.
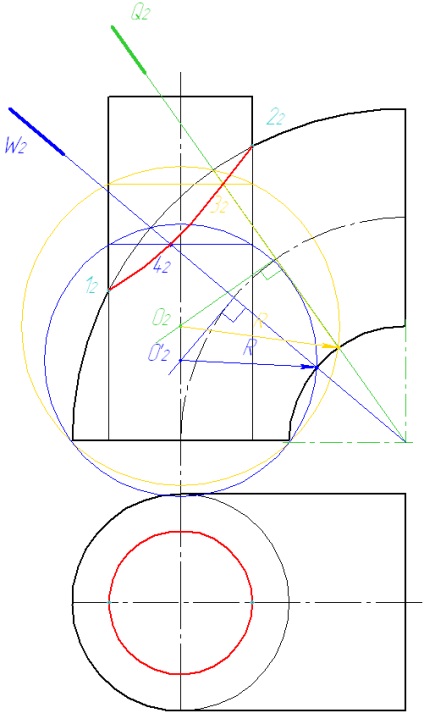
З'єднуємо отримані точки плавною кривою. Знаходимо другу проекцію лінії перетину.
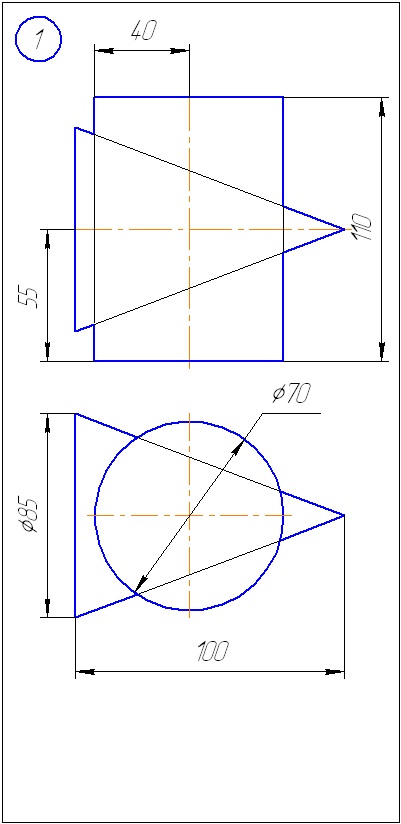
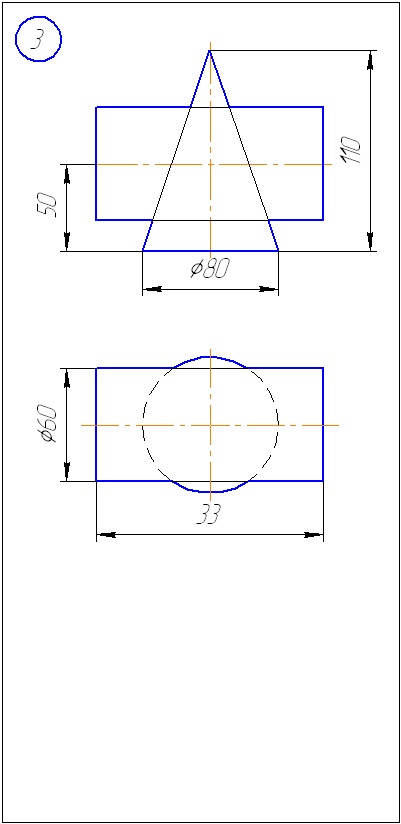
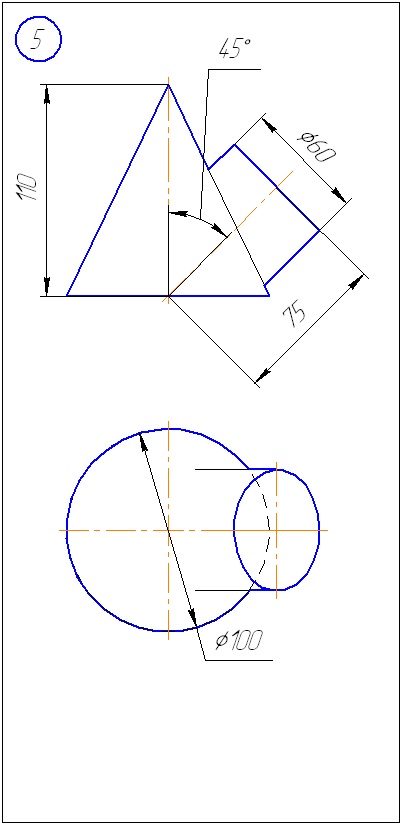
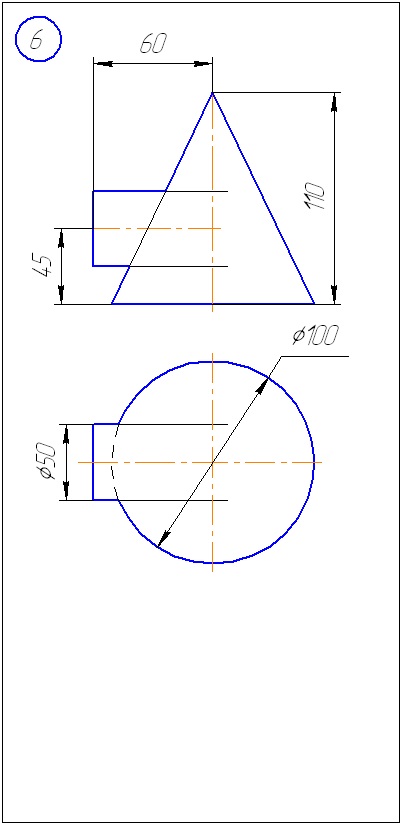
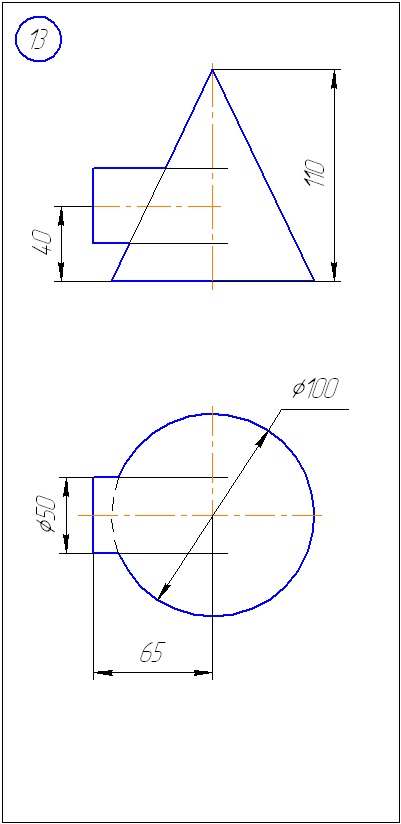
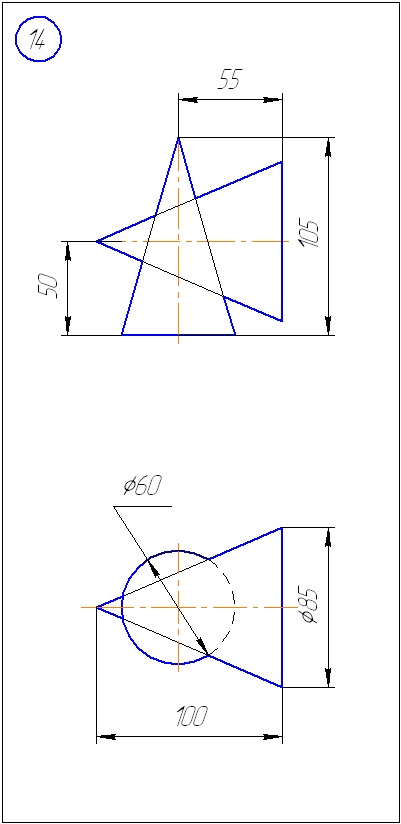
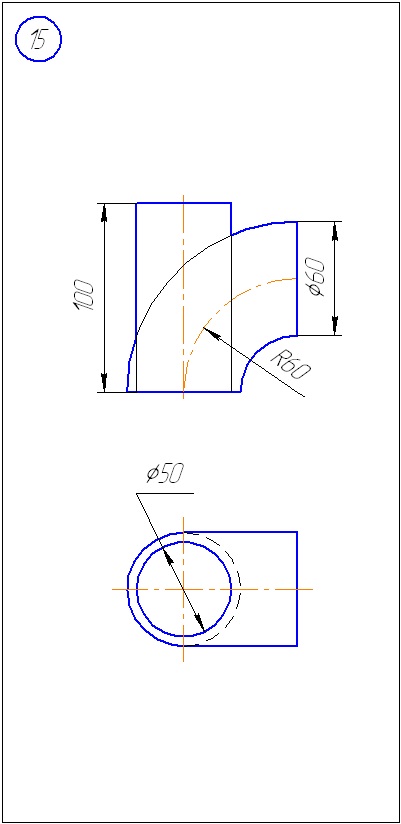
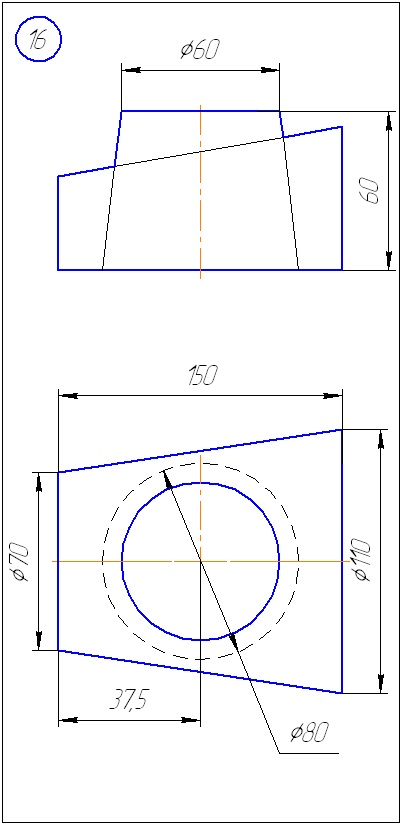
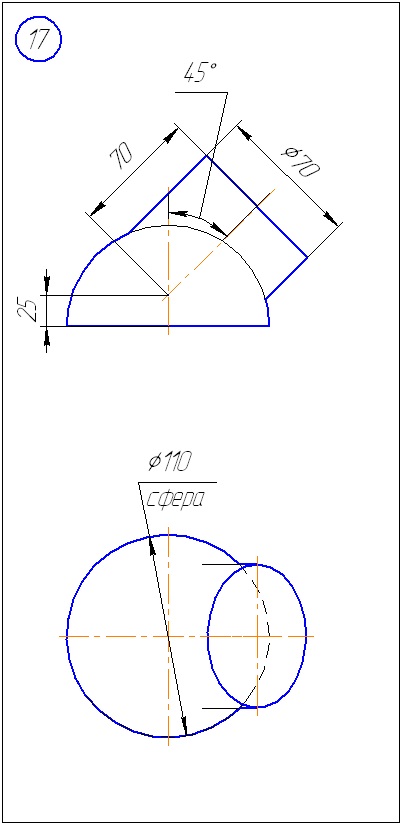
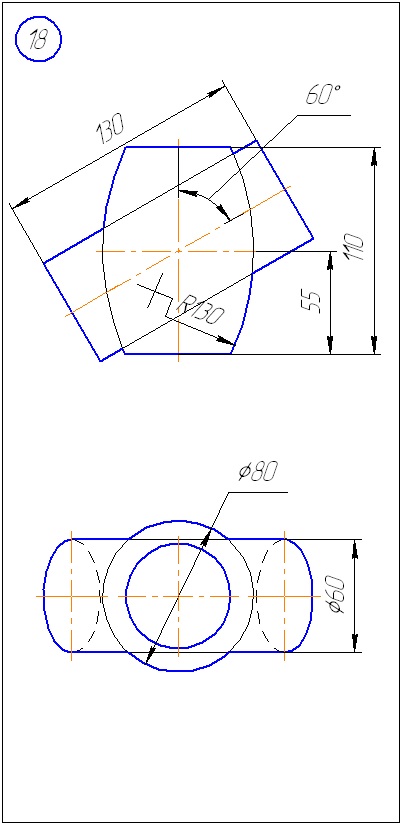
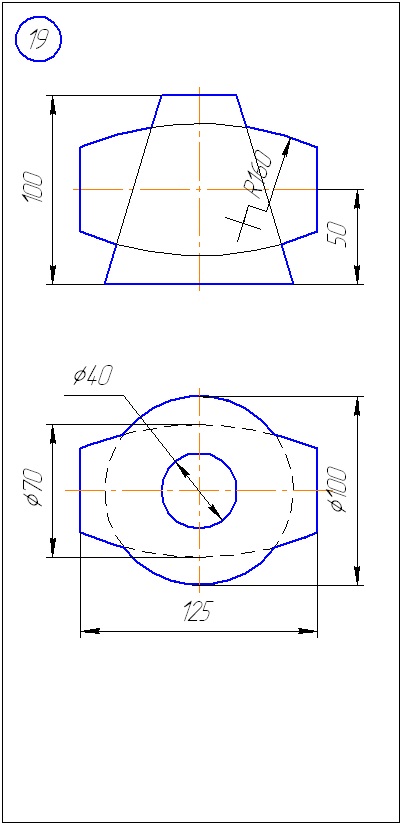
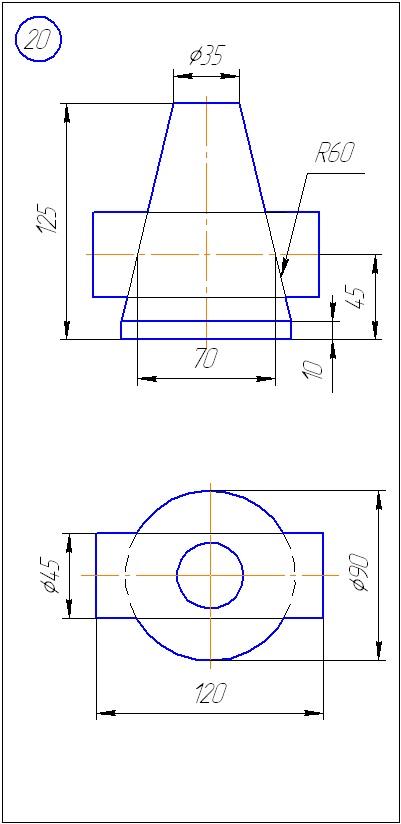
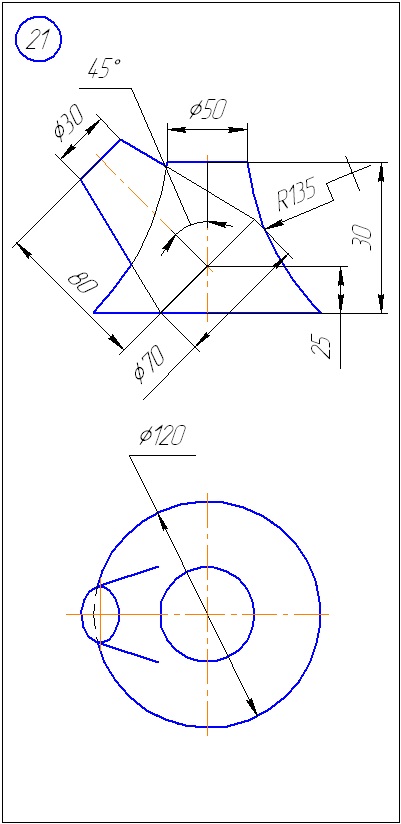
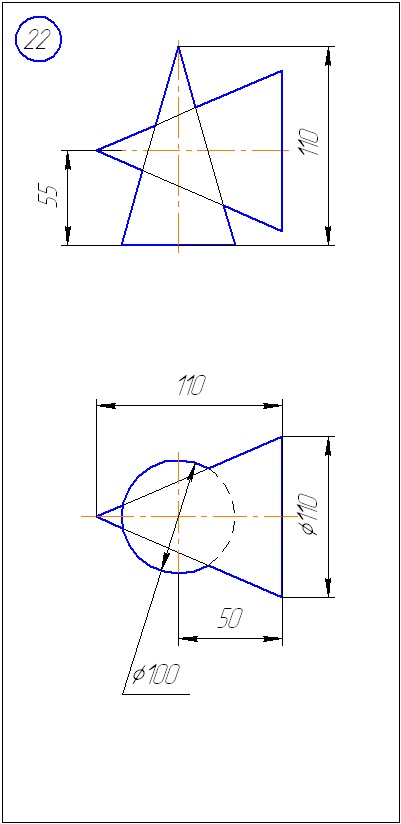
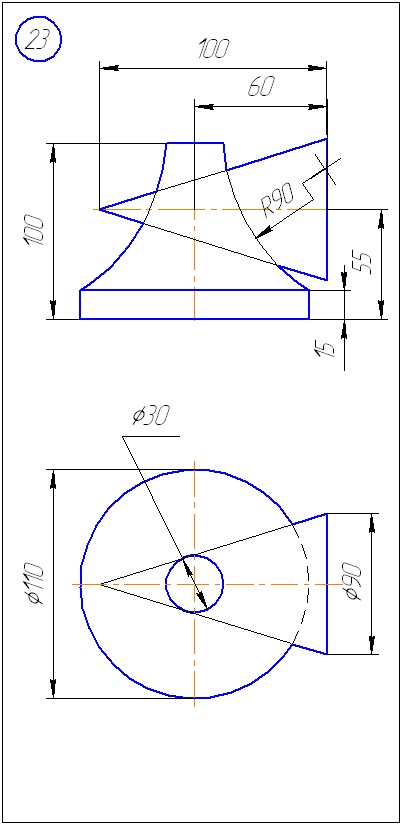
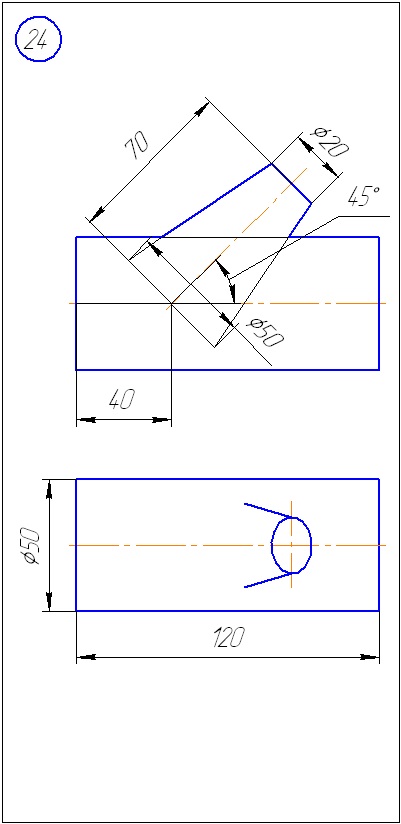
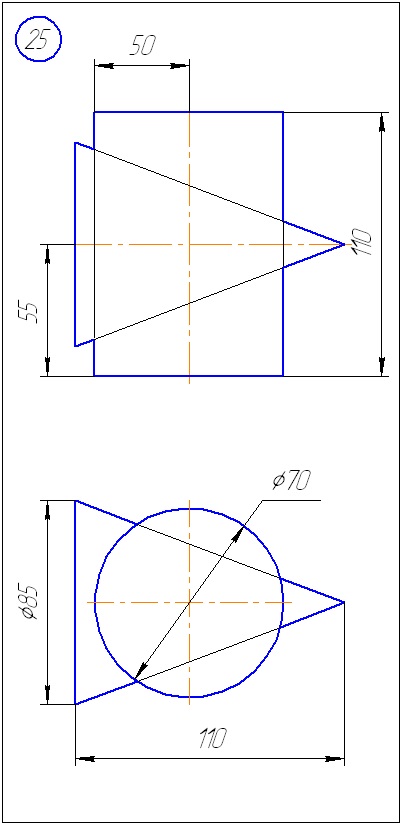
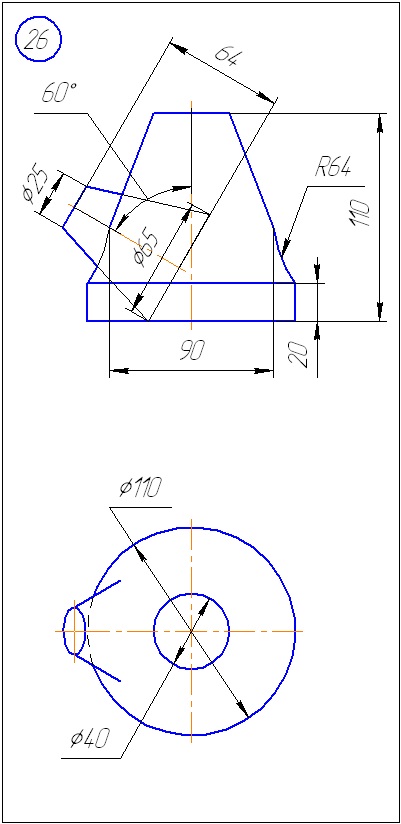
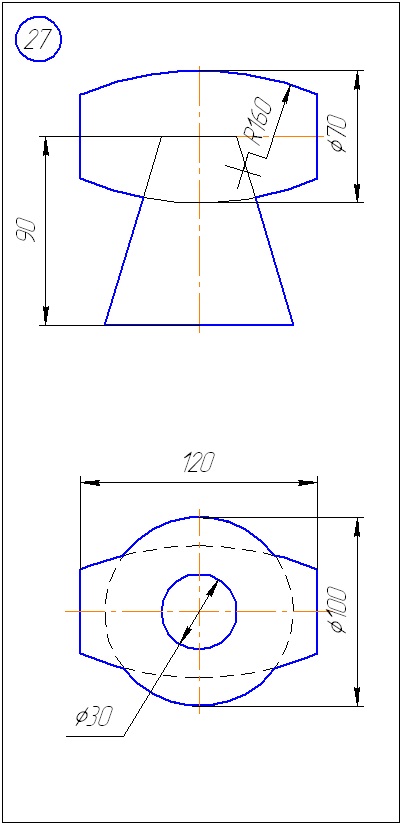
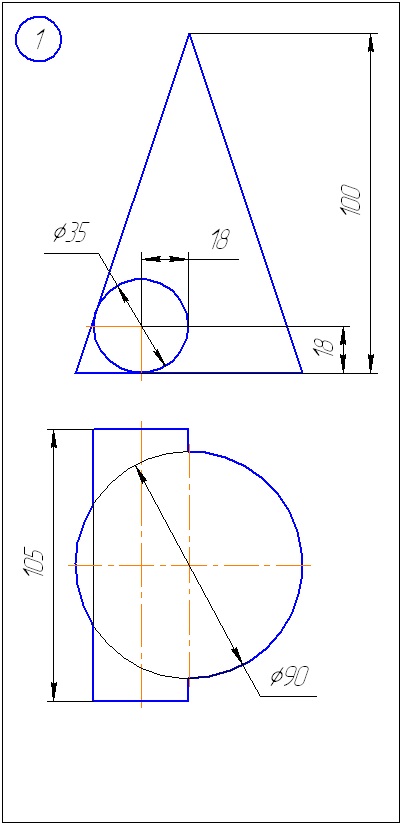
Додаток А - Варіанти завдань до задачі 1 (метод січних площин)
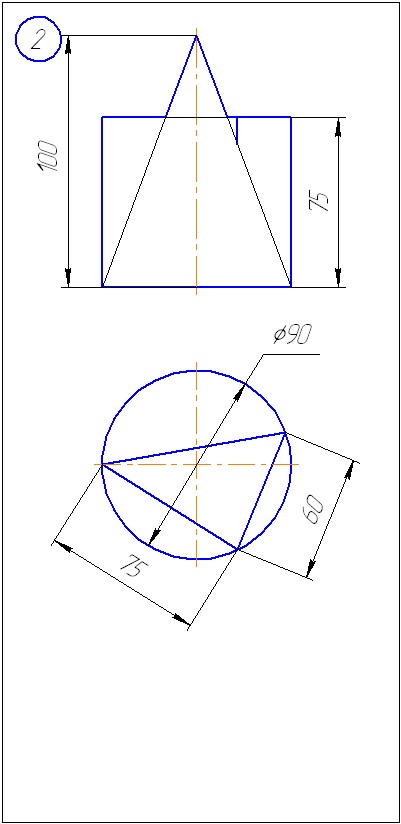
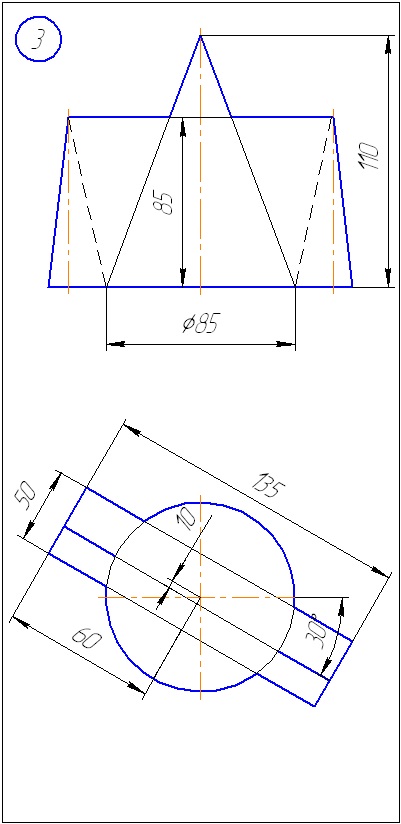
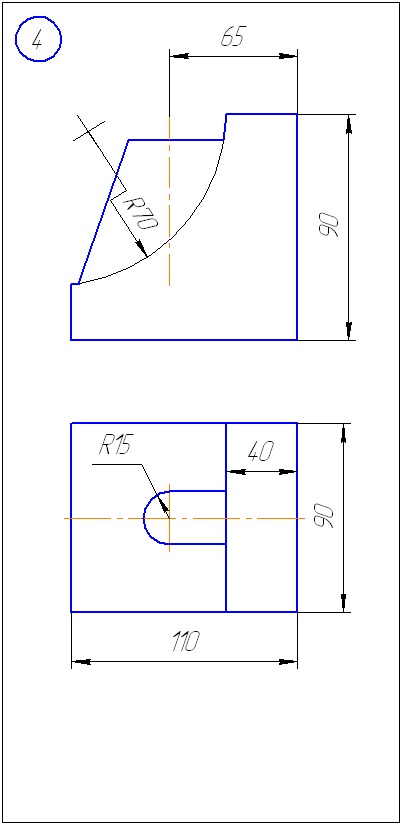
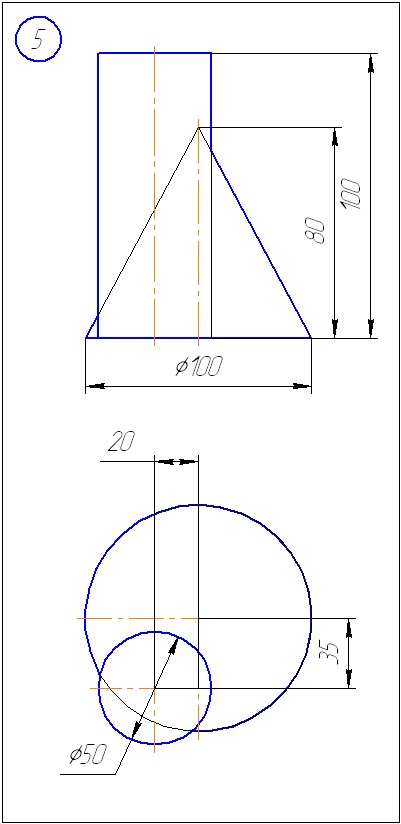
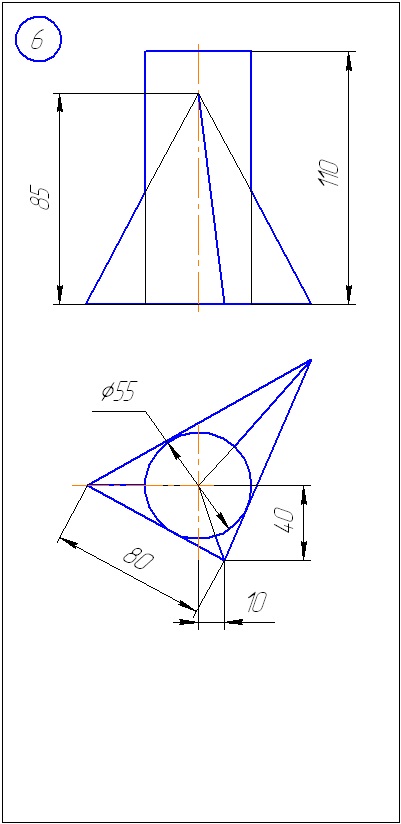
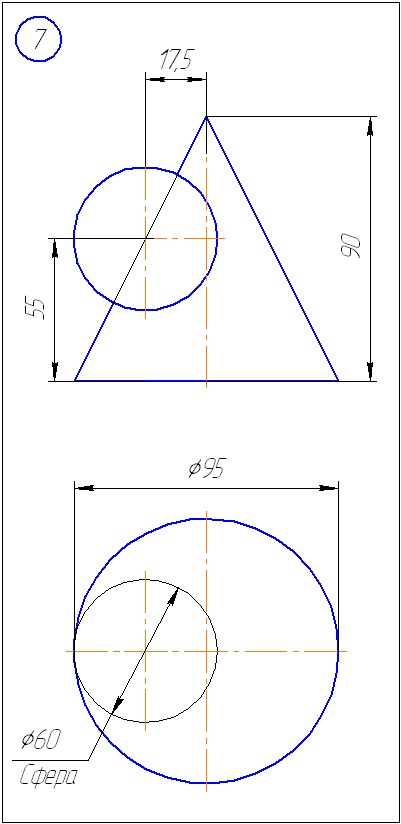
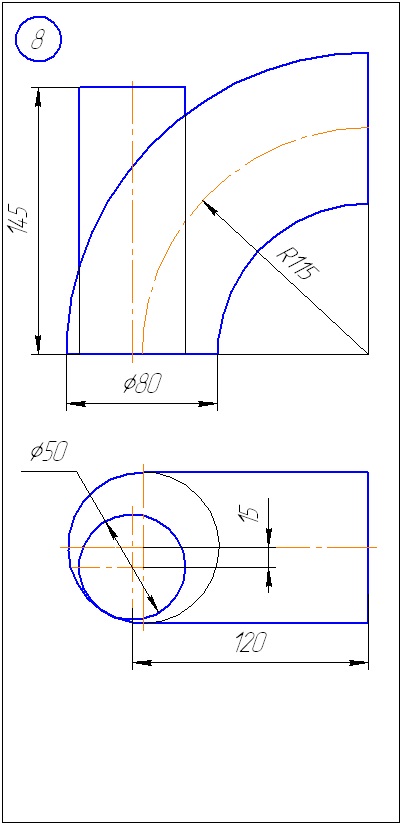
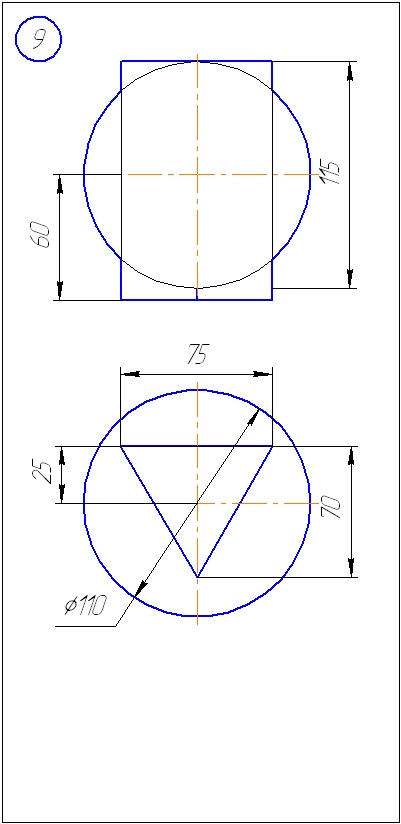
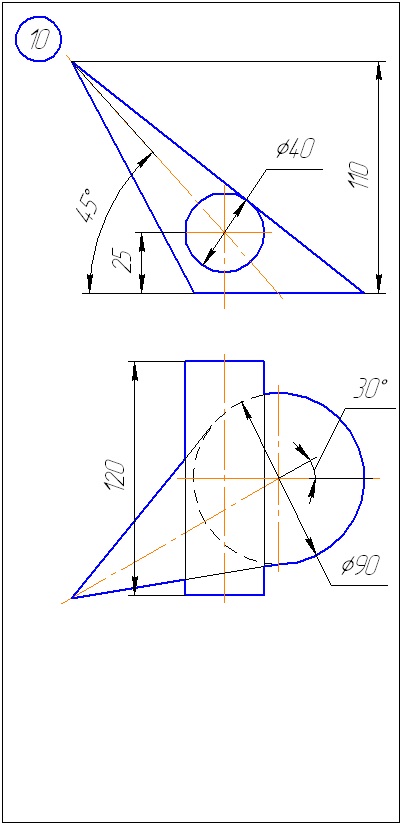
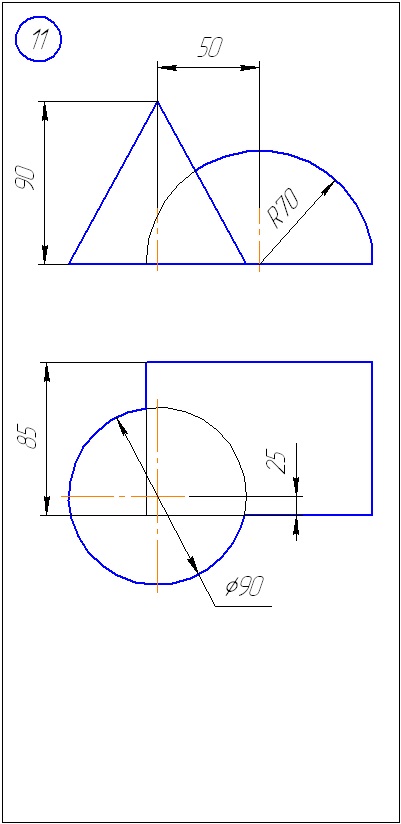
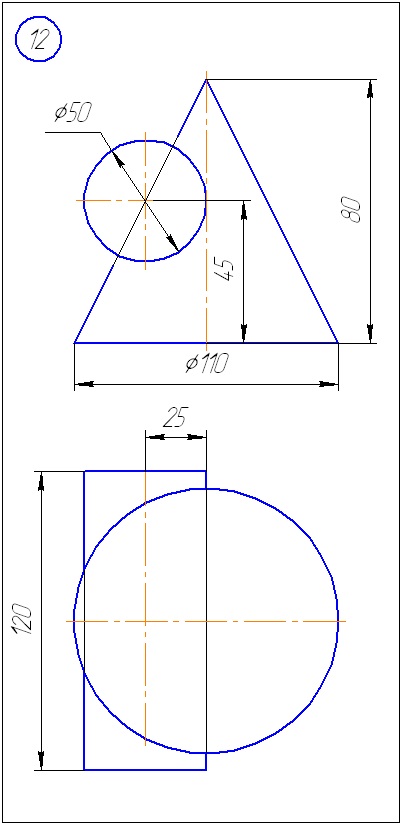
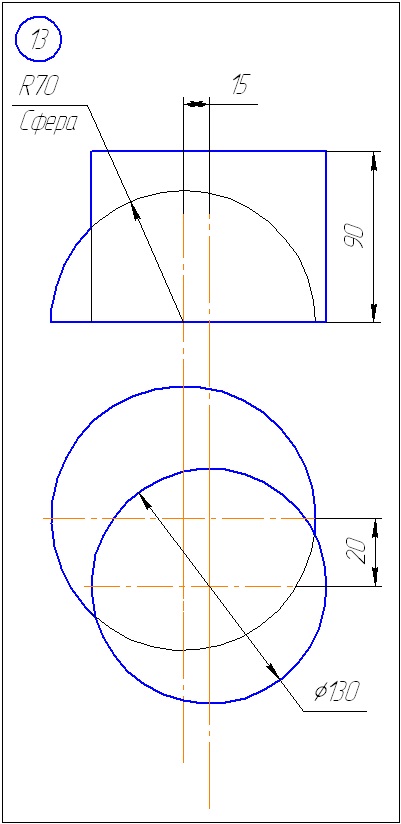
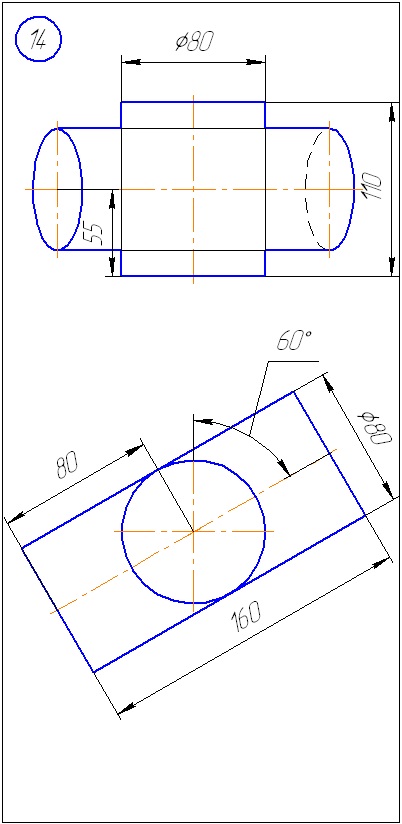
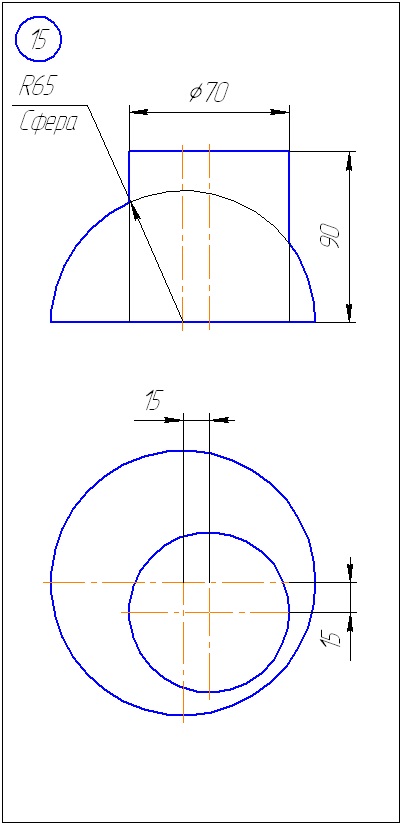
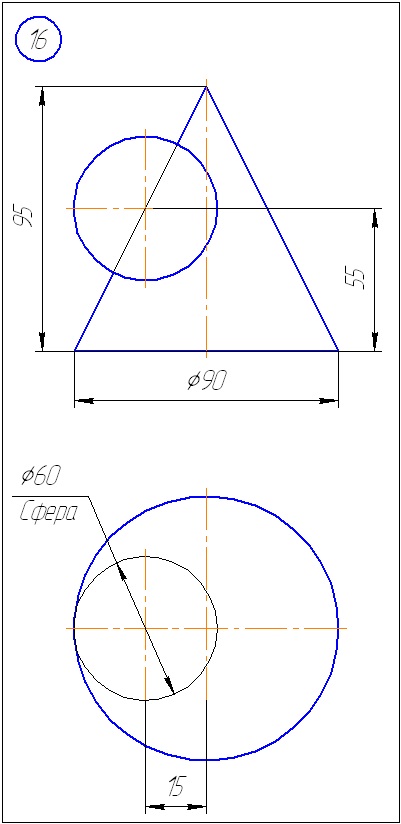
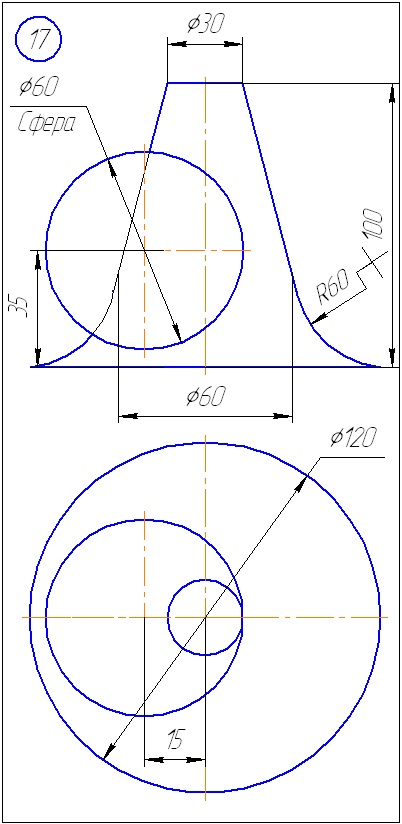
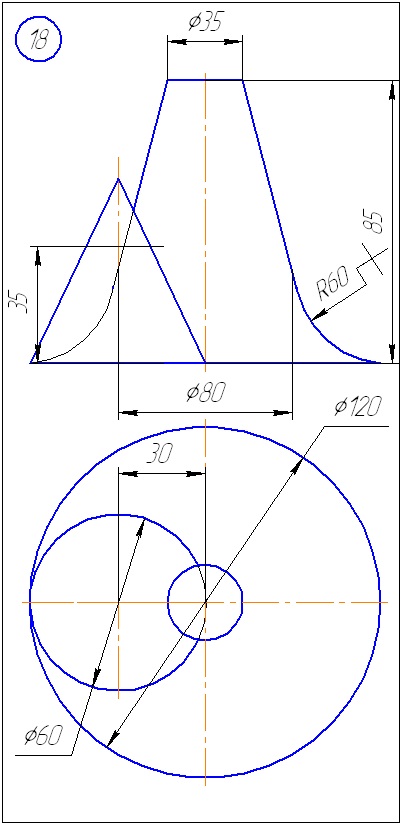
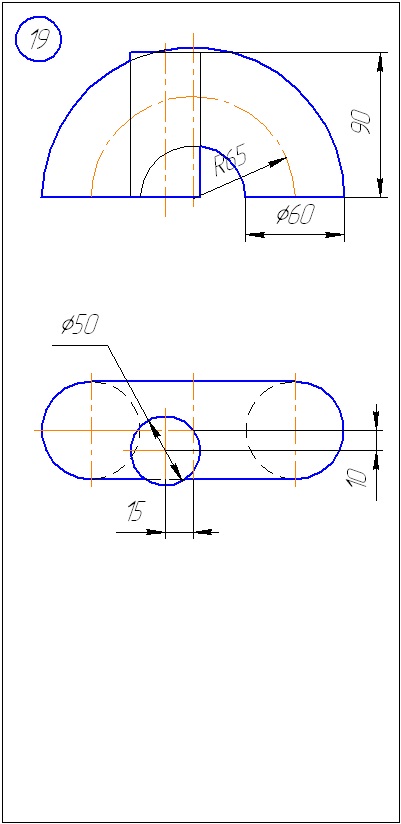
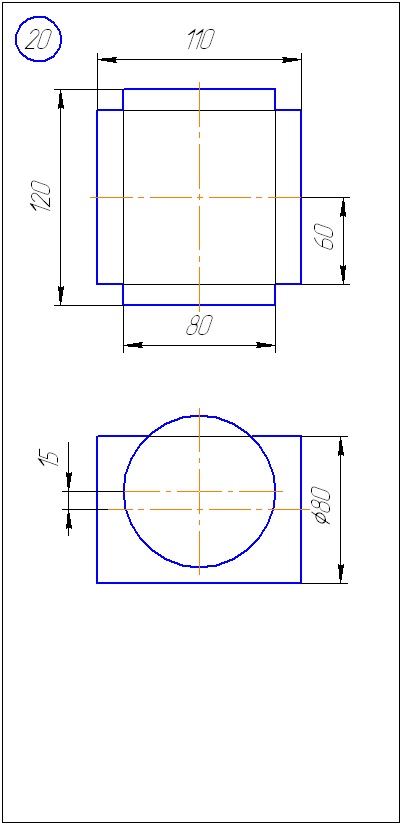
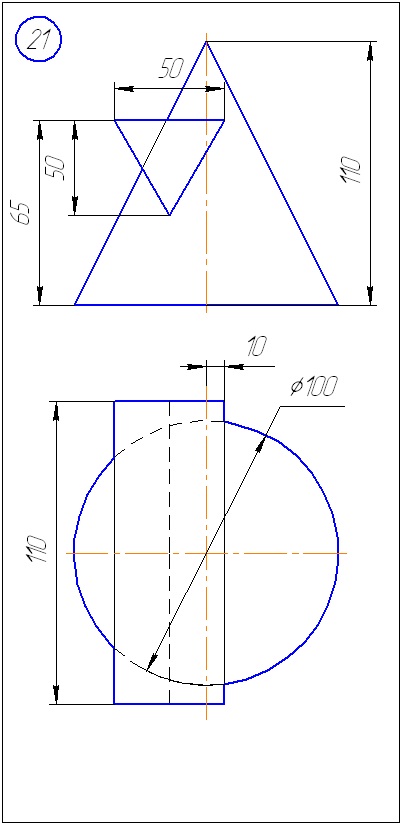
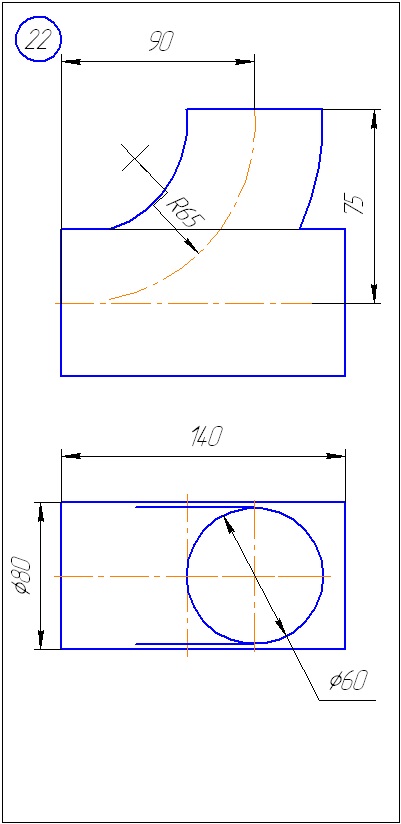
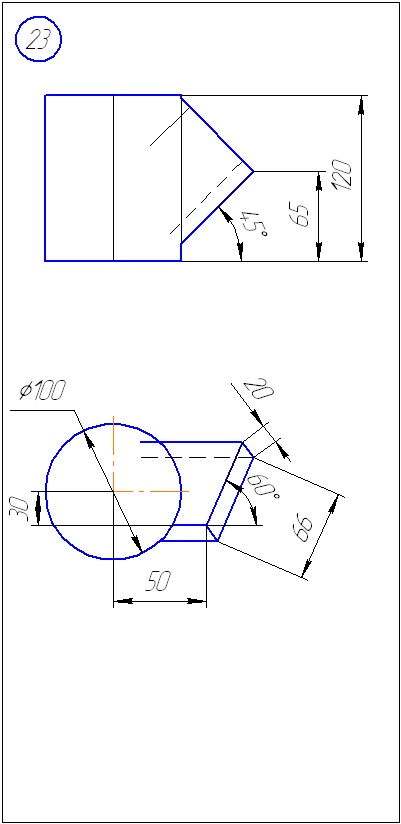
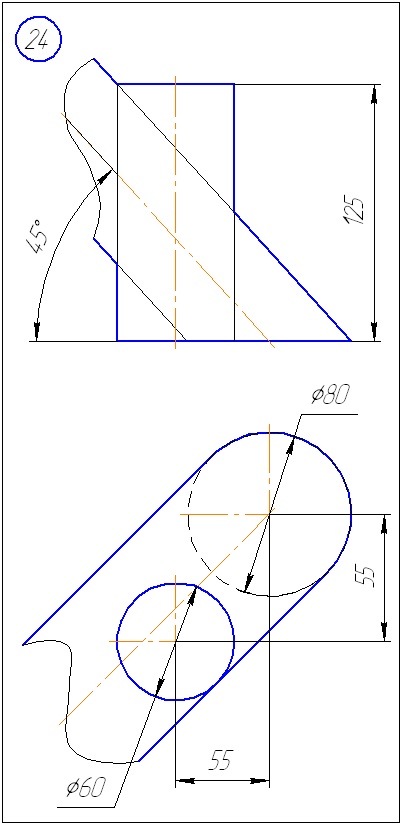
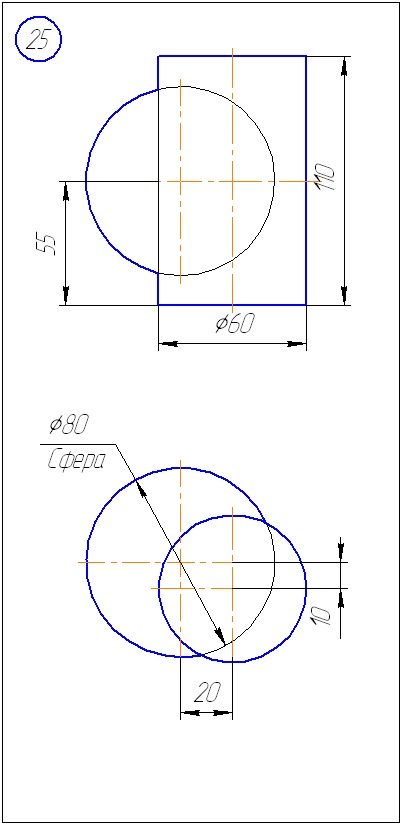
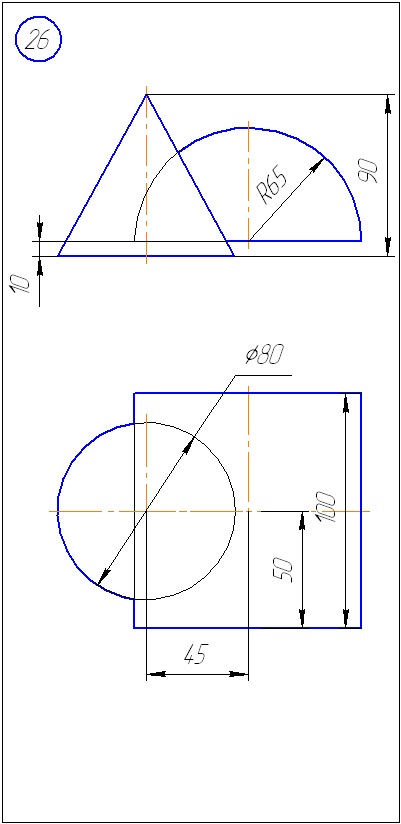
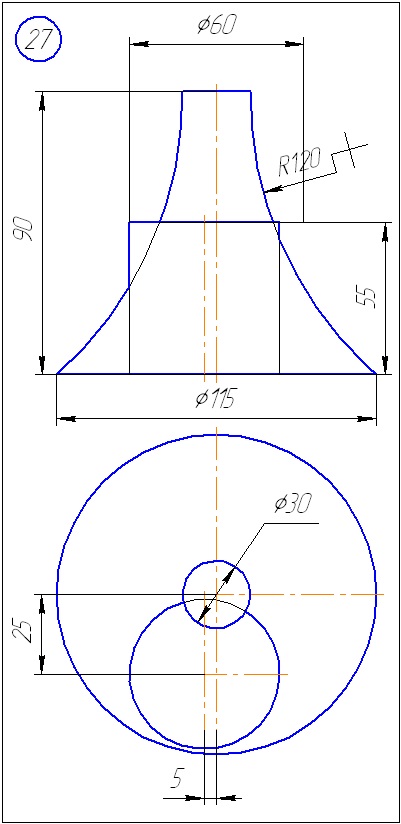
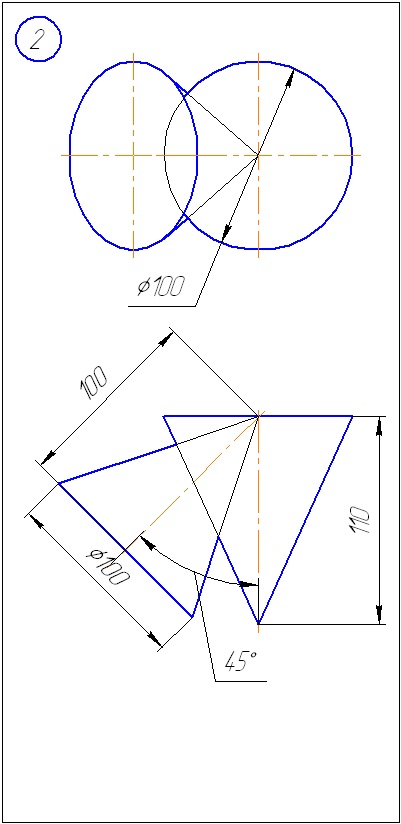
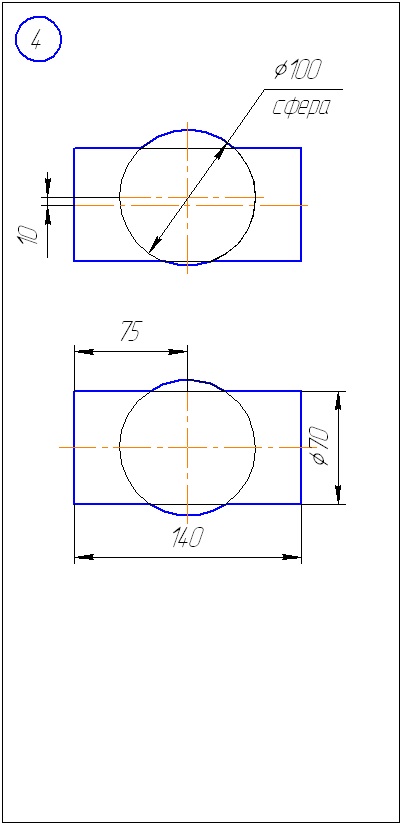
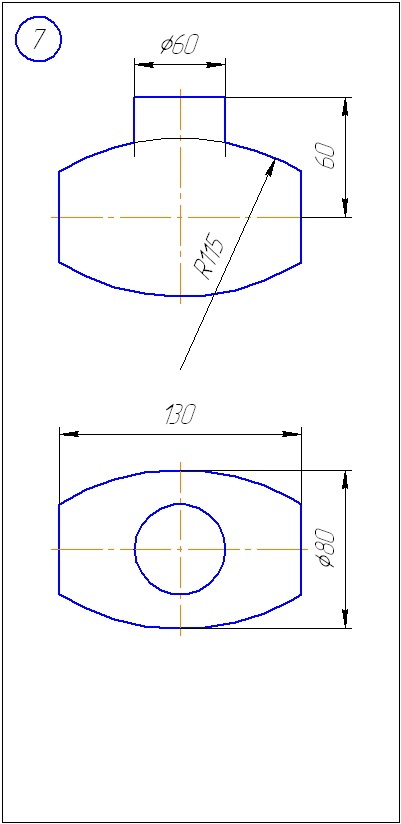
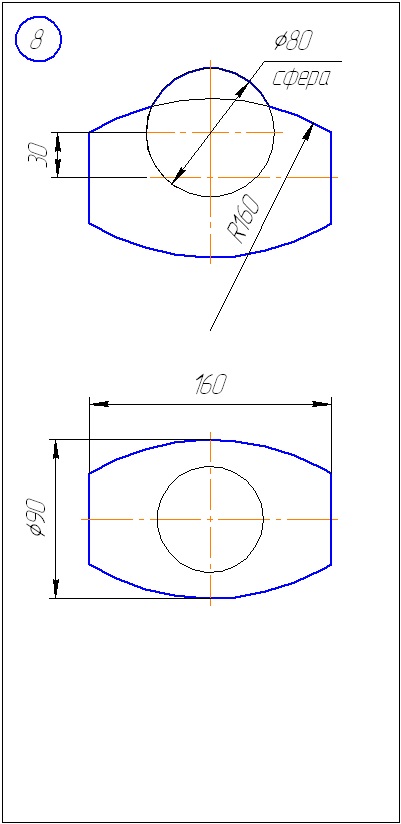
Додаток Б - Варіанти завдань до задачі 2 (метод сфер)