Рішення однорідного лінійного рівняння з постійними коефіцієнтами.
Назад Зміст Вперед
рівняння виду
називається однорідним лінійним рівнянням з постійними коефіцієнтами. Його рішення складається на основі коренів характеристичного рівняння.
Цьому однорідному рівнянню відповідає характеристичне рівняння:
.
і нехай воно має коріння. тоді:
1) Якщо - дійсний корінь кратності 1, то йому відповідає доданок загального рішення виду
2) Якщо - дійсний корінь кратності k, то йому відповідає доданок загального рішення виду, де - многочлен (з невизначеними коефіцієнтами) ступеня на 1 менше кратності кореня, тобто наприклад, якщо корінь. то
3) Якщо - пара сполучених комплексних коренів, то
4) Якщо - комплексно пов'язані коріння кратності k, тоді, відповідно, перед косинусом і синусом пишуться не просто константи, а многочлени ступені k-1.
приклади:
Приклад 1.
Вирішити рівняння:
Складемо і вирішимо характеристичне рівняння
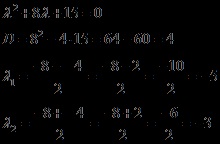
Отримали два дійсних кореня кратності 1 (тобто їх по 1 шт.), Тоді загальне рішення однорідного рівняння буде мати вигляд:
відповідь:
Приклад 2.
Вирішити рівняння:
Складемо і вирішимо характеристичне рівняння
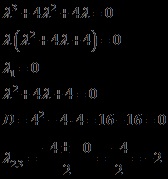
Отримали три дійсних кореня.
(Кратность- 1) і (тому що їх 2 шт. Однакових, то кратність - 2). тоді загальне рішення однорідного рівняння буде мати вигляд:
Зауважте, тому що корінь -2 має кратність 2, то співмножником у відповідному доданку буде не просто С, а загальний вигляд многочлена першого ступеня, тобто ступеня, на 1 меншій кратності кореня.
відповідь:
Приклад 3.
Вирішити рівняння:
Складемо і вирішимо характеристичне рівняння
Отримали пару комплексних сполучених коренів, кратності 1
. тоді загальне рішення однорідного рівняння буде мати вигляд:
відповідь:
Приклад 4.
Вирішити рівняння:
Складемо і вирішимо характеристичне рівняння
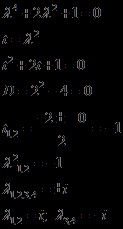
Отримали дві однакові Парф комплексних сполучених коренів, тобто кратності 2
. тоді загальне рішення однорідного рівняння буде мати вигляд:
відповідь: