Традиційний висновок рівняння Ван-дер-Ваальса
Стан певної маси будь-якої речовини можна описати за допомогою трьох параметрів: тиску \ (p \). обсягу \ (V \) і температури \ (T \). Ці параметри пов'язані між собою. Їх взаємозв'язок описується рівнянням стану. яке в загальному випадку має вигляд: \ [F \ left (\ right) = 0. \] Конкретний вид рівняння залежить від властивостей речовини. Наприклад, розріджений газ при досить високій температурі добре описується моделлю ідеального газу. Рівнянням стану для нього є відоме рівняння Клапейрона (\ (1799-1864 \)). запропоноване в \ (1834 \) році: \ [pV = \ fracRT. \] Тут \ (m \) - маса газу, \ (M \) - молярна маса (тобто маса одного благаючи даного газу), \ ( R \) - універсальна газова постійна. Для одного моля газу це рівняння приймає наступний вигляд: \ [pV = RT. \] Проведені пізніше експерименти виявили відхилення в поведінці реальних газів від законів ідеального газу. Ці результати були узагальнені голландським фізиком Яном Дідерик Ван-дер-Ваальса (\ (1837-1923 \)). який в \ (1873 \) році запропонував більш точне рівняння стану реального газу. Воно називається рівнянням Ван-дер-Ваальса і в розрахунку на один моль записується у вигляді \ [\ left (>> \ right) \ left (\ right) = RT. \] Дане рівняння враховує сили тяжіння і відштовхування, що діють між молекулами. Сили тяжіння враховуються завдяки пристінкового ефекту. Дійсно, для частинок, що знаходяться у внутрішній області, сили тяжіння з боку інших молекул в середньому компенсовані. Однак для частинок поблизу стінок посудини виникає нескомпенсованих сила тяжіння \ (f, \) спрямована всередину судини. Ця сила, з одного боку, пропорційна концентрації частинок \ (n \) в посудині, а з іншого боку - пропорційна концентрації частинок в пристеночном шарі. В результаті отримуємо: \ [f \ sim \ sim \ frac >>, \] де \ (n \) - концентрація молекул в посудині, \ (V \) - обсяг \ (1 \) благаючи газу.
Розглянутий ефект тяжіння молекул пристінкового шару призводить до зменшення тиску на стінки посудини. При формальному переході від рівняння Клапейрона до рівняння Ван-дер-Ваальса це відповідає заміні \ [p \ to p + \ frac >>, \] де \ (a \) - коефіцієнт, що залежить від конкретного газу і розмірів судини.
Сили відштовхування між молекулами в моделі Ван-дер-Ваальса враховуються дуже просто: передбачається, що молекули мають форму кулі радіуса \ (r \) і не можуть наблизитися один до одного на відстань між центрами, менше ніж \ (2r. \) Можна вважати , що навколо однієї з двох молекул існує "заборонений" (виключений) обсяг (рисунок \ (1 \)), рівний \ [\ frac \ pi \ right) ^ 3> = 8 \ cdot \ frac \ pi. \] Отже, в розрахунку на одну молекулу виключений обсяг дорівнює \ [= 4 \ cdot \ frac \ pi = 4, \] де \ (\) - обсяг однієї молекули.
В результаті. якщо в рівнянні Клапейрона обсяг простору, доступного для руху молекул, дорівнював \ (V, \) то тепер він стає рівним \ [V - = V - b, \] де \ (\) - число Авогадро (яка дорівнює кількості молекул в одному молі газу), \ (b \) - виключений обсяг, обумовлений відштовхуванням молекул.

Рис.2 Ян Дідерик Ван-дер-Ваальса
Припускаючи, що сили тяжіння і відштовхування молекул діють спільно і замінюючи \ (p \) і \ (V \) новими виразами, отримуємо з рівняння Клапейрона рівняння Ван-дер-Ваальса: \ [\ left (>> \ right) \ left (\ right) = RT. \]
Ізотерми рівняння Ван-дер-Ваальса
При фіксованій температурі рівняння Ван-дер-Ваальса описує залежність \ (p \ left (V \ right). \) На площині \ (pV \) така залежність зображується у вигляді сімейства ізотерм. кожна з яких відповідає певній температурі. Для дослідження характеру цієї залежності перетворимо рівняння Ван-дер-Ваальса до наступного вигляду: \ [>>> \ right) \ left (\ right) = RT \;> \ right | \ Cdot,> \; \; + A> \ right) \ left (\ right) = RT,> \; \; + AV - pb - ab - RT = 0,> \; \; - \ left (\ right) + aV - ab = 0 \;> \ right |: p,> \; \; - \ left (>> \ Right) + \ frac
V - \ frac>
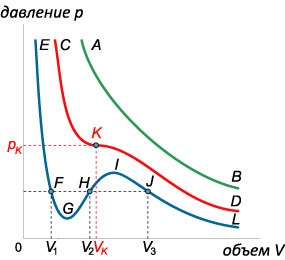
= 0.> \] При фіксованому значенні \ (p \) отримане рівняння є рівнянням третього ступеня по змінній \ (V \). Відомо, що кубічне рівняння може мати \ (1 \) або \ (3 \) дійсних кореня. Перший випадок зустрічається при високих температурах \ (T \) (зелена ізотерма \ (AB \) на малюнку \ (3 \)). При зниженні температури на изотерме з'являється хвилеподібний ділянку. У цьому випадку існує три кореня (синя ізотерма \ (EFGHIJL \)). Перехід між двома типами ізотерм відбувається при певній температурі \ (\) яка називається критичною температурою.
> \ Right) + \ frac
V - \ frac>
= 0 \] має записуватися як \ [> \ right) ^ 3> = 0. \] Розкриваючи куб різниці і прирівнюючи коефіцієнти при відповідних ступенях \ (V, \) знаходимо вирази для критичних параметрів: \ [> \ right) ^ 3 > = 0,> \; \; - 3 + 3V - V_K ^ 3 = 0.> \] Врахуємо, що в критичній точці \ (p = \), \ (T =. \) Отже, отримуємо: \ [- \ left (>
> \ Right) = - 3 \\ \ frac >> = 3V_K ^ 2 \\ - \ frac >>> = - V_K ^ 3 \ end \ right.,> \; \; b + \ frac>
= 3 \\ \ frac >> = 3V_K ^ 2 \\ \ frac >>> = V_K ^ 3 \ end \ right ..> \] Розділимо третє рівняння на друге: \ [\ require >> \ cdot \ cancel >> = \ frac >>>>>,> \; \; = 3b.> \] З другого рівняння визначаємо \ (: \) \ [= \ frac >> = \ right)> ^ 2 >>>> = >>.> \] Нарешті, з першого рівняння знаходимо критичну температуру \ ( : \) \ [= \ frac - b> \ right) >>> = \ right) \ cdot \ frac >>>>> = >>.> \] Отже, критичні параметри газу в моделі Ван-дер-Ваальса залежать лише від величин \ (a, b \) і визначаються формулами \ [= 3b,> \; \; \; = \ Frac >>,> \; \; \; = \ Frac >>.> \] Зауважимо, що ми знайшли критичні величини без використання похідної. Можна показати, що в критичній точці з параметрами \ (\), \ (\), \ (\) перша і друга похідна функції \ (p \ left (V \ right) \) дорівнюють нулю (дивіться Приклад \ (1 \) ).
Наведене рівняння стану
Використовуючи критичні параметри \ (\), \ (\) і \ (\) можна перейти до безрозмірних змінних: \ [>>,> \; \; \; >>,> \; \; \; >>> \] і переписати рівняння Ван-дер-Ваальса в наведеній формі. \ [\; P = \ pi, \; T = \ tau,> \; \; + \ Frac> \ right)> ^ 2 >>>> \ right) \ left (- b> \ right) = R \ tau,> \; \; >>> + \ frac \ right)> ^ 2 >> >> \ right) \ left (\ right) = R \ tau \ cdot \ frac >>,> \; \; >>> \ right) \ left (\ right) = 8 \ tau.> \] Дане рівняння є більш універсальним, ніж вихідне рівняння Ван-дер-Ваальса. Ізотерми для різних речовин, побудовані відповідно до наведеного рівнянням, будуть збігатися при однакових значеннях \ (\ tau. \) Стани різних тіл, які описуються однаковими наведеними параметрами \ (\ pi, \) \ (\ varphi, \) \ (\ tau, \) називаються відповідними станами. Якщо два будь-яких тіла або речовини мають будь-якими двома однаковими наведеними параметрами, то вони мають і третю однакову величину. Це універсальна властивість називається законом відповідних станів. Розглянемо ще один цікавий інваріант. Оскільки в моделі Ван-дер-Ваальса критичні величини \ (\), \ (\), \ (\) виражаються лише через два параметра \ (a \) і \ (b, \) ми можемо скласти комбінацію цих величин, що не залежить від \ (a \) і \ (b. \) Можна записати наступне співвідношення: \ [>>>>> = >>>>>>>>> = \ cdot \ cancel \ cancelR >> \ cancel \ cdot 8 \ cancel >>> = >> \; \; \; \; \; \; \ Frac >> R >>> = = 0,375.> \] Це відношення називається критичним коефіцієнтом і не залежить ні від яких величин, що характеризують ту чи іншу речовину, тобто є інваріантною величиною.Фазовий перехід "газ-рідина" і метастабільні стани
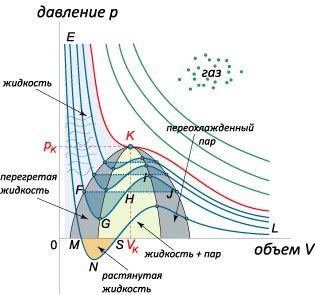
Розглянемо знову рівняння Ван-дер-Ваальса при температурах не вище критичної: \ (T 0, \) що відповідає нестабільного стану речовини. При малої флуктуації обсягу \ (dV> 0 \) тиск газу буде також зростати (так як \ (dp> 0 \)), що призведе до вибухового розширення газу. При негативній флуктуації \ (dV 0 \)) знаходяться всередині області, обмеженої спінодаль. Область діаграми між спінодаль і бінодалью в принципі відповідає критерію стійкості \ (\ large \ frac >> \ normalsize 0.> \] Видно, що дискримінант завжди позитивний, тобто квадратне рівняння має два дійсних кореня. Вони виражаються наступною формулою: \ [> = \ fracRT >>> \ right) >>> = RT >>> RT> \ right) >>> = RT >> \ right) >> RT >>.> \] Перший корінь \ (\) зі знаком мінус в чисельнику не має фізичного сенсу, оскільки \ (0 \) парабола, відповідна чисельнику похідної, буде направлена гілками верх. Тому похідна при переході через правий корінь \ (\) змінює знак з мінуса на плюс. Це означає, що точка \ (\) є мінімумом функції \ (pV: \) \ (=>. \)
Таким чином, при стисненні розрідженого газу Ван-дер-Ваальса при постійній температурі твір \ (pV \) спочатку зменшується, досягаючи мінімального значення \ (\ right) _>, \) а потім починає зростати. Перша стадія пояснюється домінуванням сил тяжіння між молекулами, а друга стадія пов'язана з посиленням вкладу відразливих сил.Деякі гази мають досить низькі значення температури Бойля. Наприклад, для гелію \ (He \) вона становить \ (= 22,6 \; \ text, \) Для неону \ (Ne \) вона дорівнює \ (= 122,1 \; \ text. \) Отже, при кімнатних температурах такі гази демонструють монотонну залежність \ (pV \) від \ (V. \)