Інтерференційні смуги рівної товщини в тонкій плівці, тобто темні або світлі смуги відповідні постійному значенню товщини плівки (d), можна спостерігати в повітряному прошарку між дотичними один з одним плоскою поверхнею пластинки і опуклою сферичною поверхнею лінзи (див. рис.5).
При цьому товщина повітряного прошарку поступово збільшується від центру лінзи до її країв. При нормальному (перпендикулярному поверхні) падінні світла смуги рівної товщини мають вигляд концентричних кіл, які отримали назву кілець Ньютона.
Якщо на лінзу падає пучок монохроматичного світла, то світлові хвилі, відбиті від верхньої і нижньої меж повітряного прошарку, интерферируют між собою.
Так як, на відміну від вище наведеного прикладу, відображення світлової хвилі відбувається в точці В від розділу середовища повітря-скло, а не скло-повітря, як на рис.4, то λ / 2 додається до доданку L1 і формула (19), в початковій її частині придбає вигляд:
Тобто, оптична різниця ходу, в цьому випадку дорівнює подвоєною товщині повітряного зазору (2d) (показник заломлення воздухаn = 1).
В результаті отримаємо:
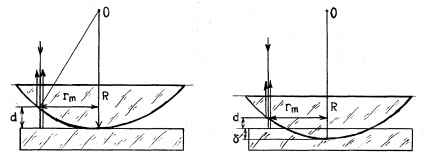
Рис.5. Схема виникнення Рис.6. облік деформації
кілець Ньютона лінзи
Темні кільця утворюються там, де оптична різниця ходу дорівнює непарному числу півхвиль (см.16):
тобто при товщині зазору
де m = 0,1,2,3. - номер кільця.
Радіус m-ного темного кільця (rm) визначається з треугольнікаAОС (см.ріс.5)
де R-радіус кривизни лінзи. Вважаючи величину повітряного зазору в місці виникнення кілець малої, (т.е.d «R) можна записати:
З цієї формули видно, що радіус кривизни лінзи можна знайти, вимірявши радіус кільця Ньютона і величину повітряного зазору в місці виникнення кільця. Радіус кілець Ньютона можна виміряти, скориставшись мікроскопом, що має вимірювальну шкалу. Щоб не вимірювати величину зазору (до речі, не зрозуміло, як це зробити експериментально), можна скористатися інтерференційним умовою виникнення темних кілець (24).
Тоді радіус кривизни лінзи можна виразити через радіус кільця Ньютона, довжину хвилі використовуваного світла і номер вимірюваного кільця:
Використання формули (28) для визначення радіуса кривизни може привести до помилки, тому що в точці дотику лінзи і скляної пластинки можлива деформація лінзи за величиною порівнянна з довжиною хвилі світла, тому використання висновків, заснованих на рис.5 (див. формули 26,27,28), буде некоректним.
Експериментально спостережувана величина повітряного зазору може бути менше теоретичної величини, отриманої з рис.5 на величину деформації скляної пластинки і лінзи (δ) (див. Рис.6). Тому в реальному експерименті в формулу (27) замість товщини повітряного зазору (d) необхідно підставити суму товщини повітряного зазору і величини деформації лінзи і скляної пластинки (d + δ) .Враховуючи, що умова виникнення темного кільця (24) визначається лише товщиною зазору, отримаємо наступну формулу, що зв'язує радіуси кілець Ньютона з радіусом кривизни лінзи:
Експериментально зручніше замість радіуса кільця Ньютона вимірювати його діаметр (Dm) .І тут формула (29) матиме вигляд:
З (30) видно, що квадрат діаметра кільця Ньютона (Dm2) пропорційний порядковому номеру кільця (m) .Якщо побудувати графік залежності Dm2 = f (m), то експериментальні точки повинні лежати на одній прямій, і тангенс кута нахилу цієї прямої (α ) буде дорівнює 4Rλ Таким чином, для знаходження радіуса кривизни лінзи необхідно, використовуючи графік залежності Dm2 = f (m), знайти
а потім розрахувати радіус кривизни лінзи за формулою:
Внаслідок деформації в центрі лінзи спостерігається кругле темна пляма, відповідне нульовий товщині повітряного зазору. Вимірявши діаметр центрального темної плями (кільця Ньютона, номер якого m = 0), можна знайти величину деформації лінзи за формулою: