Обчислимо роботу, використовуючи в цей раз не другий закон Ньютона. а явне вираз для сил взаємодії між тілами залежно від відстаней між ними. Це дозволить нам ввести поняття потенційної енергії - енергії, залежної від швидкостей тіл, а від відстаней між тілами (або від відстаней між частинами одного і того ж тіла).
Обчислимо спочатку роботу сили тяжіння при падінні тіла (наприклад, каменю) вертикально вниз. У початковий момент часу тіло перебувало на висотеh1 над поверхнею Землі, а в кінцевий момент часу - на висотеh2 (рис.6.5). Модуль переміщення тіла.
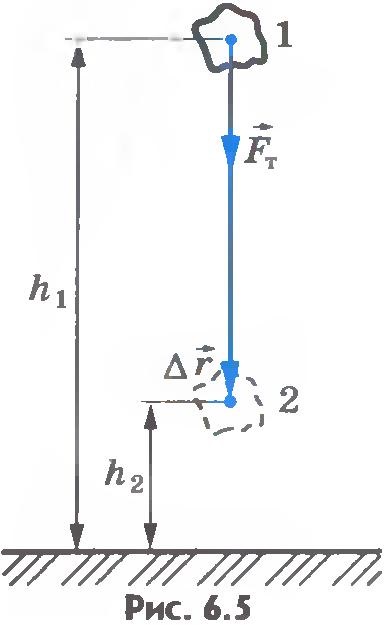
Напрями векторів сили тяжіння і переміщення збігаються. Згідно з визначенням роботи (див. Формулу (6.2)) маємо
Нехай тепер тіло кинули вертикально вгору з точки, розташованої на висоті h1, над поверхнею Землі, і воно досягло висоти h2 (рис.6.6).
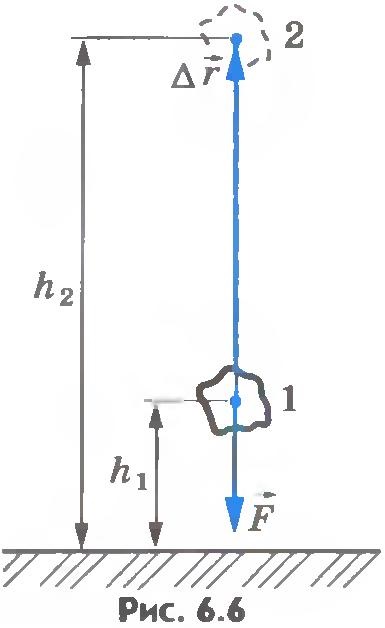
Вектори і спрямовані в протилежні сторони, а модуль переміщення. Роботу сили тяжіння запишемо так:
Якщо ж тіло переміщається по прямій так, що напрямок переміщення становить кут з напрямком сили тяжіння (рис.6.7), то робота сили тяжіння дорівнює:
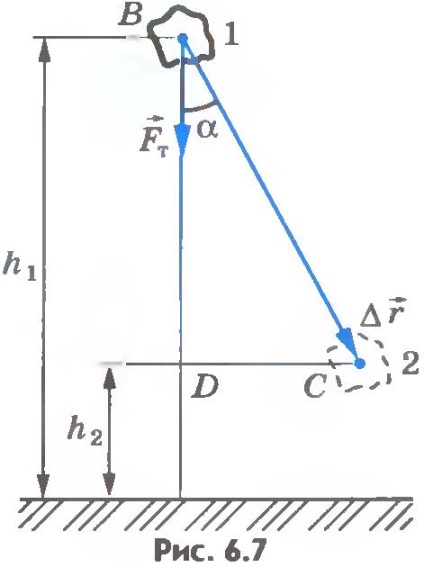
З прямокутного трикутника BCD видно, що. отже,
Формули (6.12), (6.13), (6.14) дають можливість помітити важливу закономірність. При прямолінійному русі тіла робота сили тяжіння в кожному випадку дорівнює різниці двох значень величини, що залежить від положень тіла в початковий і кінцевий моменти часу. Ці положення визначаються висотами h1 і h2 тіла над поверхнею Землі.
Більш того, робота сили тяжіння при переміщенні тіла масою m з одного положення в інше не залежить від форми траєкторії, по якій рухається тіло. Дійсно, якщо тіло переміщається уздовж кривої ВС (рис.6.8), то, представивши цю криву у вигляді ступінчастою лінії, що складається з вертикальних і горизонтальних ділянок малої довжини, побачимо, що на горизонтальних ділянках робота сили тяжіння дорівнює нулю, так як сила перпендикулярна переміщенню , а сума робіт на вертикальних ділянках дорівнює роботі, яку зробила б сила тяжіння при переміщенні тіла по вертикальному відрізку довжиною h1 -h2.
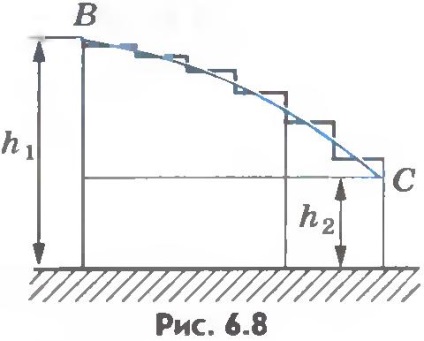
Таким чином, робота при переміщенні уздовж кривої ВС дорівнює:
При русі тіла по замкнутій траєкторії робота сили тяжіння дорівнює нулю. Справді, нехай тіло рухається по замкнутому контуру ВСDМВ (рис.6.9). На ділянках ВС і DМ сила тяжіння робить роботи, рівні по абсолютній величині, але протилежні за знаком. Сума цих робіт дорівнює нулю. Отже, дорівнює нулю і робота сили тяжіння на всьому замкнутому контурі.
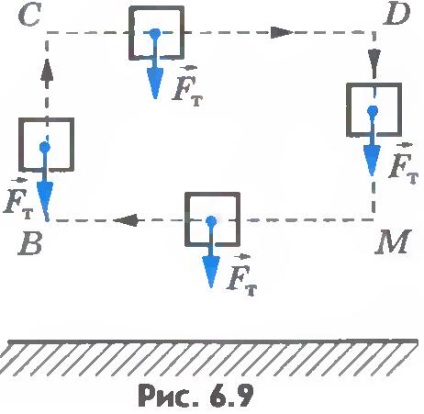
Сили, що володіють такими властивостями, називають консервативними.
Отже, робота сили тяжіння не залежить від форми траєкторії тіла; вона визначається лише початковим і кінцевим положеннями тіла. При переміщенні тіла по замкнутій траєкторії робота сили тяжіння дорівнює нулю.
Повний список тим з фізики. календарний план по всім предметам згідно шкільної програми, домашнє завдання, курси та завдання з фізики для 10 класу
Якщо у вас є виправлення або пропозиції до даного уроку, напишіть нам.
Якщо ви хочете побачити інші коригування та побажання до уроків, дивіться тут - Освітній форум.