С.В. Усатіков, кандидат фіз-мат наук, доцент; С.П. Грушевський, кандидат фіз-мат наук, доцент; М.М. Кириченко, кандидат соціологічних наук
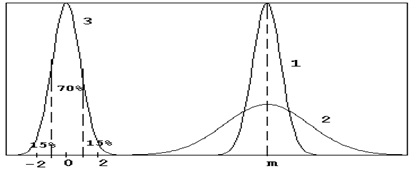
Рис.1 Щільність розподілу ймовірностей нормального закону
1,2 - графіки з одним середнім m і різними стандартними відхиленнями s. причому s 1
3 - графік при m = 0, s = 1 для Z - закону і зразковим розподілом площ під кривою.
Під аргументом x тут можна розуміти найрізноманітніші числові величини, що не піддаються передбаченню до проведення експерименту: зріст, вага, число помилок при тестуванні, розумовий розвиток, схильність до правопорушень і будь-які інші, що виникають як результат складання багатьох незалежних (або слабо залежних) і порівнянних по порядку свого впливу випадкових впливів. Функція f (x) показує наступну важливу інформацію: ймовірність числової величиною х прийняти значення більше числа а і менше числа в дорівнює площі під кривою f (x) на відрізку [a, b] (рис.1). Зрозуміло, це стосується будь-яких a і b, близьких між собою або далеких, розташованих в будь-якому місці прямий х. Крім того, площа під всієї кривої f (x) дорівнює 1, тобто ймовірність для х потрапити на пряму дорівнює 1, і ця подія достовірне (це властивість ще називається умовою нормування).
У нормального закону два параметра, повністю його визначають: числа m і s. Число m є середня величина для цікавлять нас числових показників: середнє зростання, середня вага і т.п. Змінюючи m. можна т здійснювати паралельний перенос кривої f (x) уздовж осі х. Видно також, що найбільш вірогідна поява числа х в експерименті поблизу m. площа під f (x) на будь-якому відрізку, що містить m, найбільша.
Число s є середнє відхилення числового показника х від числа m: чим менше s. тим "крутіше" стає "пагорб" f (x) (рис.1) і тим менше ймовірність для х сильно відрізнятися від m. Навпаки, при великих s "пагорб" f (x) розтікається по "рівнині" і з майже однаковою ймовірністю х може з'явитися як поблизу m. так і як завгодно далеко від m.
Якщо числовий показник х перерахувати в число Z за таким правилом:
то все "пагорби" f (x) перетворяться в криву 3 закону Z Гаусса на рис.1. Тоді всі крапки ± 1 для Z відповідає точкам m ± s для х, а точки ± 3 для Z - точкам m ± 3s для х. За розподілом площ під кривою 3 видно, що на відрізку [-3,3] зосереджено приблизно 99,7% всієї площі під кривою f (x). Звідси випливає так зване правило "трьох s" для закону Z: з імовірністю р = 0,997 випадкова величина х відхиляється від то все "пагорби" f (x) перетворяться в криву 3 закону Z на рис.1. Тоді всі крапки ± 1 середньої m (вліво або вправо) не більше ніж на 3s.
Тепер настав момент пояснити, чому так багато уваги приділяється "горбу" f (x) на рис.1. У теорії ймовірностей доведено теорему, абсолютно справедливо названа центральною граничною теоремою. У грубих рисах, сума великого числа (практично більше 7 - 10) незалежних випадкових величин, порівнянних по порядку свого впливу на розсіювання суми, підпорядковується нормальному закону. Наприклад, зростання людини, на який впливають дуже багато факторів, серед яких в масі немає домінуючих за своїм впливом.
З початку ХХ століття виявився дуже корисним введений Пирсоном закон c 2 (рис.2): в страховій справі, в з'ясуванні торгового попиту або популярності політиків і т.п.
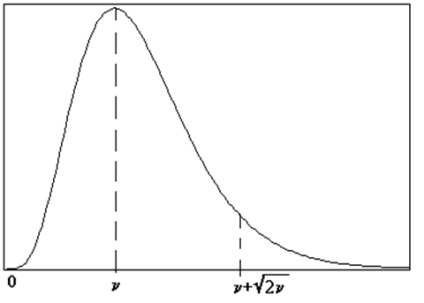
Рис.2. Щільність розподілу ймовірностей законаc 2, з n ступенями свободи.
Під аргументом х тут розуміється сума n незалежних доданків в квадраті, кожне з яких підпорядковується нормальному Z- закону з m = 0 і s = 1. Ясно, що при великих n (практично при n> 30) закон c 2 перетворюється в нормальний закон з m = n і s =
, оскільки діє теорема Ляпунова. Але найчастіше доданків не більше 10. Число n називається числом ступенів свободи. Сенс f (x) такий же, як і в нормальному законі: ймовірність числової величиною х = c 2 потрапити в заданий діапазон дорівнює площі під кривою f (x). Так, площа під кривою на відрізку від 0 до n +
становить понад 90% всієї площі під всієї кривої f (x). Звідси следут правило "трьох s" для закону c 2: з імовірністю рі 0,9 випадкова величина х = c 2 не перевищує величини n + Ц 2n (очевидно, c 2 не може бути негативним).
Нарешті, необхідно згадати закон t Стьюдента, отриманий з нормального закону і законаc 2. Випадкова величина t виходить з дробу у чисельнику якого стоїть випадкова величина Z Гаусса з m = 0 і s = 1, а в знаменнику - випадкова величина c 2 з n ступенями волі. За -колишньому при великих n закон Стьюдента переходить в нормальний закон (практично при n и 30). Але навіть при невеликих n вигляд кривої щільності розподілу ймовірностей для t дуже схожий на криву 3 рис.1. Різниця в тому, що замість s = 1 для Z необхідно брати s = n / (n -2), т.е.среднее відхилення t від m = 0 більше, ніж середнє відхилення Z від m = 0. Відповідно "пагорб" закону t більш пологий, ніж "пагорб" закону Z.
Всі матеріали в розділі "Математика"