Проведемо за допомогою Mathcad апроксимацію для заданих точок за допомогою степеневої та лінійної функції. Визначимо суму квадратів відхилень для вузлових точок (рис. 13):
Для статечної функції ця величина дорівнює 43,684.
Для лінійної функції ця величина дорівнює 740,782.
Можна зробити висновок, що за допомогою степеневої функції ми отримуємо більш точне значення.

Рис.13. Апроксимація точок в Mathcad
Побудуємо на одній координатній площині графіки апроксимуючих функцій (рис. 14).
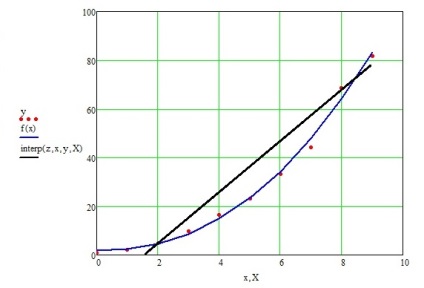
Ріс.14.Графікі аппроксимирующих функцій
Проведемо апроксимацію точок за допомогою Excel. Для цього спочатку заповнимо вихідну таблицю точок і відзначимо ці точки на графіку (рис. 15).
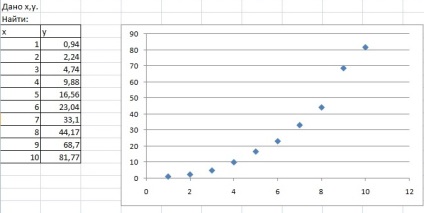
Мал. 15. Вихідні точки для апроксимації на графіку
Викличемо контекстне меню для однієї з точок на графіку і виберемо пункт «Додати лінію тренда ...». Для початку проведемо апроксимацію за допомогою степеневої функції. Для цього в діалоговому вікні «Лінія тренда» виберемо «Степенева».
Аналогічно додамо лінію тренда на основі лінійної функції. В налаштуваннях ліній тренда виставимо галочку «показувати рівняння на діаграмі». Результат представлений на рис.16. Отримали наступні аппроксимирующие функції:
Для статечної функції:
y = 0,672x 2,014 +2,072
Для лінійної функції:
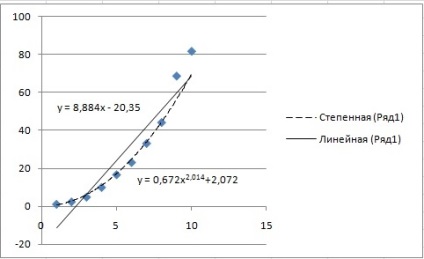
Рис.16. Отримання графіків функцій апроксимації
Визначимо суму квадратів відхилень для отриманих функцій в вузлових точках (рис. 17). отримаємо:
Для статечної функції ця величина дорівнює +178,4447864.
Для лінійної функції ця величина дорівнює 740,78208.
Отже, апроксимація набору даних статечної функції більш точна, ніж лінійної функції.
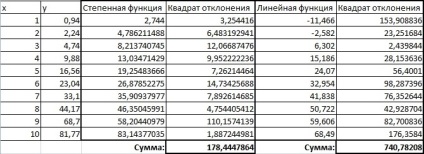
Рис.17. Розрахунок в Excel суми квадратів відхилень для аппроксимирующих функцій
При виконанні апроксимації в Mathcad і Excel отримали, що Mathcad дозволяє побудувати ступеневу аппроксимирующую функцію з можливістю задати рівняння степеневої апроксимуючої функції з вільним коефіцієнтом, що неможливо виконати в Excel. Це вказує на недоліки Excel при виконанні подібних завдань.
Знайти екстремум функції двох змінних:
в Excel і Mathcad. Побудувати графік двовимірної поверхні в Excel і Mathcad.
Побудуємо графік двовимірної поверхні в Mathcad (рис. 18)
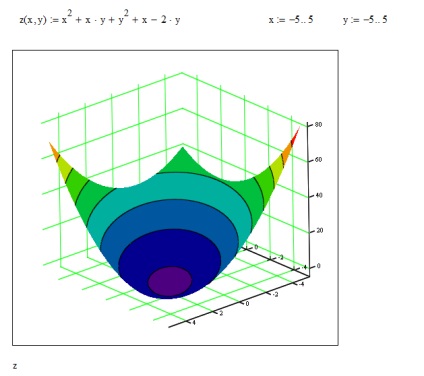
Рис.18. Побудова поверхні в Mathcad
За графіком визначаємо, що функція z має тільки один екстремум - точку мінімуму. Скористаємося функцією Minimize, за початкове наближення точки мінімуму візьмемо; . В якості обмежень вкажемо інтервали для і. Отримали рішення. (Рис. 19)
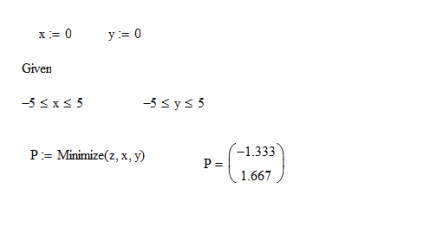
Ріс.19.Нахожденіе мінімальних значень за допомогою Mathcad
Для виконання спочатку проведемо табуляцію функції з кроком 1 на інтервалі з футболу (рис. 20).
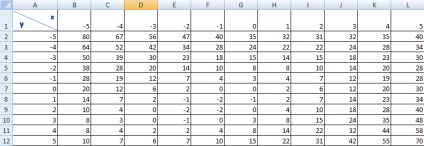
Ріс.20.Табулірованіе функції 2-х змінних в Excel
На основі отриманої таблиці будуємо поверхню (рис. 21).
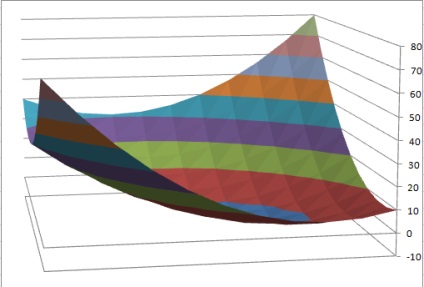
Рис.21. Графік функції 2-х змінних в Excel
Excel і Mathcad дозволяють раціонально вирішувати інженерні завдання, поставлені перед користувачем. В результаті проведеної роботи можна зробити висновок про перевагу Mathcad над Excel при вирішенні математичних завдань, які були наведені в роботі.
Виконана курсова робота дозволила закріпити вже наявні знання про Excel і Mathcad, а також дозволила дізнатися більше про можливості цих пакетів програм. Крім того, на основі практичних знань з'явилася можливість сказати про переваги і недоліки використовуваних, при вирішенні завдань, програм.