Для розрахунку руху механічної системи маятник-вантаж застосуємо рівняння динаміки поступального руху для вантажу, закріпленого на нитки, і динаміки обертального руху для маятника.
Вантаж масою m рухається з прискоренням під дією результуючої сил тяжіння і сили натягу нитки. Запишемо другий закон Ньютона в проекції на напрямок руху:
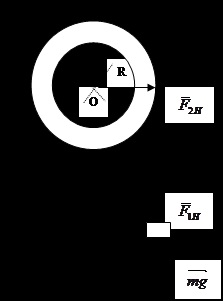
Момент сили опору щодо осі обертання спрямований у протилежний бік (до нас).
Основний закон динаміки обертального руху:
,
де - результуючий момент сил,
J - момент інерції маятника,
У скалярною формі це рівняння має вигляд (записані проекції векторів моментів сил і кутового прискорення на вісь обертання О, напрямок якої вибрано «від нас»):
Використовуючи кінематичний зв'язок лінійного і кутового прискорення. а також рівняння руху вантажу. висловимо e через вимірювані величини x і t:
Вирішимо систему рівнянь (1) і (2), для чого помножимо (1) на R і складемо з (2):
.
Висловлюємо момент інерції маятника Обербека:
Всі величини, крім МСОПР. що входять в це рівняння, відомі. Поставимо задачу експериментального визначення МСОПР.
Нехай I - момент інерції маятника Обербека без вантажів. З (4) випливає, що
В умовах експерименту. що дозволяє вважати залежність e (m) лінійної.
Цю залежність можна використовувати для експериментальної оцінки величини. Дійсно, якщо отриману експериментально залежність екстраполювати до перетину з віссю абсцис, тобто до точки на цій осі, для якої виконується (див. 5) рівність. то це дозволяє визначити як
Для визначення моменту інерції маятника I скористаємося (4), де величина МСОПР попередньо визначена з вимірів e (m) і формули (6). Підставивши вираз e з (3) і МСОПР з (6) в (4), отримуємо робочу формулу для визначення моменту інерції маятника
.
Для використовуваного в роботі маятника Обербека справедливо нерівність. З огляду на це, отримуємо:.
Для розрахунків зручно уявити момент інерції у вигляді:
Величини коефіцієнтів k: k1. k2 для відповідних діаметрів шківів D1, D2 вказуються в паспорті установки. Для визначення моменту інерції маятника необхідно виміряти час t опускання вантажу масою m.
Залежність моменту інерції маятника від відстані вантажів до осі обертання
Момент інерції маятника Обербека може бути представлений як сума моментів інерції хрестовини зі шківами (I1) і моментів інерції чотирьох тягарців, закріплених на відстанях r від осі обертання (4I2). Якщо розміри цих тягарців малі в порівнянні з r, можна вважати, що I2 = m1 r 2 - момент інерції матеріальної точки. Тоді момент інерції маятника
Цю залежність моменту інерції від відстані вантажів до осі обертання передбачається перевірити, використовуючи результати, отримані за формулою (7).
Значення можна взяти з даних експерименту для визначення моменту інерції маятника Обербека без вантажів, вважаючи, що момент сил опору залишається постійним.
Завдання до роботи:
1. Приступивши до роботи, зніміть вантажі з стрижнів, намотайте нитку на шків більшого діаметра. Для трьох значень маси підвішеного вантажу m виміряйте час опускання вантажу t для заданої відстані x. За формулою (3) розрахуйте величину кутового прискорення e для відповідних значень m.
2. Побудуйте залежність e (m). Визначте з графіка по точці його перетину з віссю абсцис значення m0. при якому e = 0. Розрахуйте за формулою (6) величину моменту сил опору МСОПР.
3. Проведіть прямі п'ятикратні вимірювання часу опускання вантажу для заданої відстані x.
4. Розрахуйте середній час t і визначте довірчу похибка вимірювання при довірчій ймовірності Р = 90%, n = 5 (див. «Вступ»).
5. Обчисліть за формулою (7) середнє значення моменту інерції хрестовини зі шківами.
6. Визначте довірчу похибка опосередкованих вимірювань моменту інерції хрестовини (див. «Вступ») і запишіть результати у вигляді.
7. Закріпивши вантажі m1 на стрижнях маятника на рівній відстані r від осі обертання, визначте яку або за допомогою лінійки, або використовуючи зазначені близько установки вихідні дані.
8. Проведіть одноразові вимірювання часу t опускання вантажу масою m (виберіть одне значення) для однієї висоти падіння при трьох різних відстанях r від осі обертання.
9. Обчисліть моменти інерції маятника з вантажами на стрижнях за формулою (7) при різних відстанях r. При цьому, як показали попередні досліди, можна з допустимою точністю використовувати в якості величини m0 її значення, знайдене раніше для хрестовини без вантажів на спицях. Порівняйте отримані дані зі значеннями моменту інерції, обчисленими за формулою (8) для відповідних значень r. Результати обчислень занесіть в таблицю вимірювань.
10. Побудуйте на одному малюнку графіки експериментально отриманої і теоретично очікуваної залежності моменту інерції маятника від r 2. проаналізуйте причини їх розбіжності.
1. Яка мета даної роботи?
2. Момент інерції, його фізичний зміст.
3. Як можна змінити момент інерції маятника Обербека?
4. Виходячи їх рівнянь динаміки поступального і обертального руху, вивести робочу формулу (7).
5. В якому випадку рух маятника є рівноприскореному?
6. Як виміряти відстань від осі обертання до центрів важків, закріплених на стрижнях?
7. Яким чином в даній роботі підтверджується лінійна залежність моменту інерції від квадрата відстані тел до осі обертання?
1. Савельєв І.В. Курс загальної фізики. - М, Наука, 1982 р Т.1. і наступні видання.
Лабораторна робота № 4
Визначення моменту інерції тіла