Середнє арифметичне значення серії вимірювань
При збільшенні n середнє значення
Формула Гаусса може бути виведена з наступних припущень:
- помилки вимірювань можуть приймати безперервний ряд значень;
- при великій кількості спостережень помилки однакового розміру, але різного знака зустрічаються однаково часто;
- ймовірність, тобто відносна частота появи помилок, зменшується зі збільшенням величини помилки. Інакше кажучи, великі помилки зустрічаються рідше, ніж малі.
Нормальний закон розподілу описується наступною функцією:
де σ - середня квадратична помилка; σ2 - дисперсія вимірювання; Хист - істинне значення вимірюваної величини.
Аналіз формули (1.13) показує, що функція нормального розподілу симетрична відносно прямої X = Xіст і має максимум при X = Xіст. Значення ординати цього максимуму знайдемо, поставивши в праву частину рівняння (1.13) Xіст замість X. Отримаємо
.
звідки випливає, що зі зменшенням σ зростає y (X). Площа під кривою
повинна залишатися постійною і рівною 1, тому що ймовірність того, що виміряне значення величини Х буде укладено в інтервалі від -∞ до + ∞ дорівнює 1 (це властивість називається умовою нормування ймовірності).
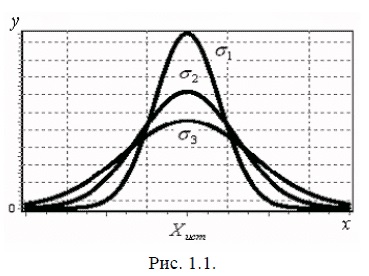
На рис. 1.1 наведені графіки трьох функцій нормального розподілу для трьох значень σ (σ3> σ2> σ1) і одному Хист. Нормальний розподіл характеризується двома параметрами: середнім значенням випадкової величини, яка при нескінченно великій кількості вимірів (n → ∞) збігається з її істинним значенням, і дисперсією σ. Величина σ характеризує розкид похибок щодо середнього значення прийнятого за дійсне. При малих значеннях σ криві йдуть більш круто і великі значення ΔХ менш вірогідні, тобто відхилення результатів вимірювань від істинного значення величини в цьому випадку менше.
Для оцінки величини випадкової помилки вимірювання існує кілька способів. Найбільш поширена оцінка за допомогою стандартної або середньоквадратичної помилки. Іноді застосовується середня арифметична помилка.
Стандартна помилка (среднеквадратическая) середнього в серії з n вимірювань визначається за формулою:
.
Якщо число спостережень дуже велике, то підвладна випадковим випадковим коливанням величина Sn прагне до деякого постійного значення σ, яке називається статистичним межею Sn:
Саме ця межа і називається середньої квадратичної помилкою. Як уже було відзначено вище, квадрат цієї величини називається дисперсією вимірювання, яка входить в формулу Гаусса (1.13).
Величина σ має велике практичне значення. Нехай в результаті вимірів деякої фізичної величини знайшли середнє арифметичне <Х> і деяку помилку ΔX. Якщо вимірювана величина схильна до випадкової помилку, то не можна беззастережно вважати, що істинне значення вимірюваної величини лежить в інтервалі (<Х> - ΔХ, <Х> + ΔХ) або (<Х> - ΔХ) <Х <(<Х> + ΔХ)). Завжди існує певна ймовірність того, що істинне значення лежить за межами цього інтервалу.
Довірчим інтервалом називається інтервал значень (<Х> - ΔХ, <Х> + ΔХ) величини X, в який за визначенням потрапляє ee справжнє значення Хист із заданою вірогідністю.
Надійністю результату серії вимірювань називають ймовірність того, що істинне значення вимірюваної величини потрапляє в даний довірчий інтервал. Надійність результату вимірювання або довірча ймовірність виражається в частках одиниці або відсотках.
Нехай α означає ймовірність того, що результат вимірювань відрізняється від істинного значення на величину, не більшу, ніж ΔХ. Це прийнято записувати у вигляді:
Р ((<Х> - ΔХ) <Х <(<Х> + ΔХ)) = α
Вираз (1.16) означає, що з імовірністю, рівною α, результат вимірів не виходить за межі довірчого інтервалу від <Х> - ΔХ до <Х> + ΔХ. Чим більше довірчий інтервал, тобто чим більше задається похибка результату вимірювань ΔХ, тим з більшою надійністю шукана величина Х потрапляє в цей інтервал. Природно, що величина α залежить від числа n проведених вимірювань. а також від задається похибки ΔХ.
Таким чином, для характеристики величини випадкової помилки, необхідно задати два числа, а саме:
- величину самої помилки (або довірчий інтервал);
- величину довірчої ймовірності (надійності).
Вказівка однієї тільки величини помилки без вказівки відповідної їй довірчої ймовірності значною мірою позбавлене сенсу, так як при цьому ми не знаємо, скільки надійні наші дані. Знання довірчої ймовірності дозволяє оцінити ступінь надійності отриманого результату.
Необхідна ступінь надійності задається характером змін, що проводяться. Середньою квадратичною помилку Sn відповідає довірча ймовірність 0.68, подвоєною середньої квадратичної помилку (2σ) - довірча ймовірність 0.95, потрійною (3σ) - 0.997.
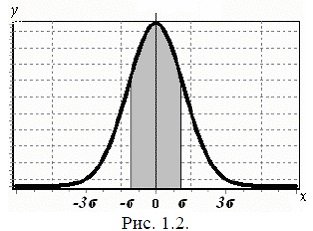
Якщо в якості довірчого інтервалу обраний інтервал (X - σ, X + σ), то ми можемо сказати, що зі ста результатів вимірювань 68 будуть обов'язково перебувати всередині цього інтервалу (рис. 1.2). Якщо при вимірюванні абсолютна похибка ΔХ> 3σ, то це вимір варто віднести до грубих похибок або промаху. Величину 3σ зазвичай приймають за граничну абсолютну похибку окремого виміру (іноді замість 3σ беруть абсолютну похибку вимірювального приладу).
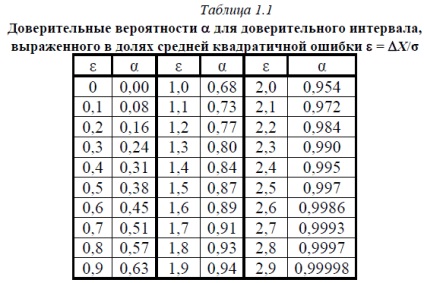
Для будь-якої величини довірчого інтервалу за формулою Гаусса може бути розрахована відповідна довірча ймовірність. Ці обчислення проведені і їх результати зведені в табл. 1.1.
Довірчі ймовірності α для довірчого інтервалу, вираженого а частках середньої квадратичної помилки ε = ΔX / σ: