Декарт говорив, що науковий метод управляє розумом людини, веде його коротким шляхом, тому він повинен обов'язково включати в себе певні правила.

Основними правилами дедуктивного методу, які запропонував Декарт, є наступні:
Перше правило - правило очевидності: «Ніколи не приймати нічого на віру, в чому з очевидністю не впевнений, тобто ретельно уникати поспішності та упередження і включати в свої судження тільки те, що представляється моєму розумові настільки ясно і чітко, що жодним чином не може дати привід для сумніву ».
Друге правило - «ділити кожну з розглядуваних мною труднощів на стільки частин, скільки буде потрібно, щоб краще їх розв'язати».
Третє правило - правило впорядкованості: «розташовувати свої думки в певному порядку, починаючи з предметів найпростіших і легкопознаваемих, і сходити мало-помалу, як по східцях, до пізнання найбільш складних, допускаючи існування порядку навіть серед тих, які в природному ході речей не передують один одному".
Нарешті, четверте правило - «робити скрізь переліки настільки повні й огляди настільки всеохоплюючі, щоб бути впевненим, що нічого не пропущено».
Ми вважаємо, що всі правила необхідно дотримуватися, але найбільш важливим є саме четверте правило.
Особливо важливо контролювати всі етапи роботи, з цією метою необхідно скласти повний перелік. У нього повинно входити велика кількість інформації, щоб торкнутися всю повноту теми досліджуваного об'єкта, і при цьому знати, що вона містить всі про дане дослідження, а так само важливо скласти перелік певних своїх дій. Огляд допомагає подивитися і проаналізувати ще раз всю цю отриману інформацію і систематизувати її в єдине ціле. Неодноразові перевірки і попередні висновки пройдених дій допоможуть виявити недоліки і виправити їх. Таким чином, повний систематизований перелік і огляд призведе до істини і успіху.
Завдання 4. На вернісажі якось раз.

Гранді Луїджі Гвідо - це італійський монах, священик, філософ, математик і інженер. У 1700-1706 і в 1714-1742 рр. - професор Пізанського університету, в 1707-1714 рр. - математик великого герцога Тосканського. Основні дослідження відносяться до теорії кривих, теоретичної і практичної механіки. Написав кілька творів з питань математики, цікавили в той час геометрів, а саме про випрямлення циклоїди, дослідження про логаріфміке і про визначення об'ємів тіл, нею створюються, і інше.
Якось раз італійський геометр Гвідо Гранді створив троянди. Троянди радують око правильними і плавними лініями, але їх обриси не примха природи - вони зумовлені спеціально підібраними математичними залежностями. Сімейство троянд Гранді описується рівнянням в полярних координатах r = a * sin (до * ф). де а і до - деякі постійні.
Зачарований результатами Гранді, німецький геометр, математик-натураліст XIX в. Б. Хабеніхта також вирішив зайнятися математичним «рослинництвом». Вважаючи, що абрис (обрис) листа або квіткової пелюстки в полярних координатах описується виразом r = f (φ), де f (φ) для кожного окремого рослини представляє певну комбінацію тригонометричних функцій, Хабеніхта шляхом численних експериментів «виростив» чудові експонати.
Таким чином, троянди Гвідо Гранді - криві, рівняння яких у полярних координатах мають вигляд: r = a * sin (k * ф). Підбираючи різні значення коефіцієнтів a і k. ви отримаєте гарні "трояндочки".
Крива, що задається формулою p = sin 3φ:

Формула кривої з подвоєною кількістю пелюсток:
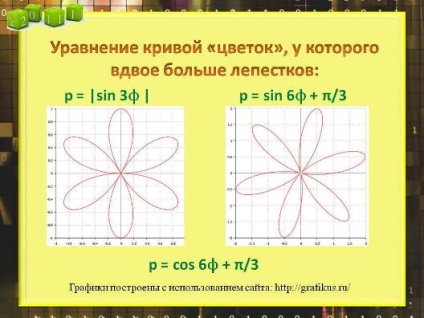
Творче завдання:
Формула для малюнка "Хризантема" і розрахунок полярних координат:
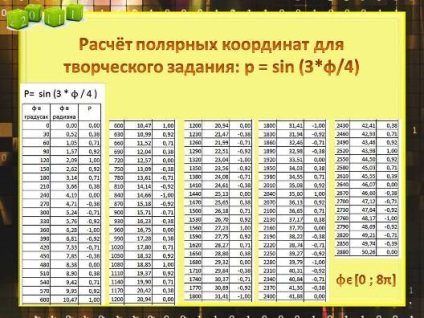
Побудова малюнка "Хризантема":

Формула для малюнка "Восьмілістнік" і розрахунок полярних координат:
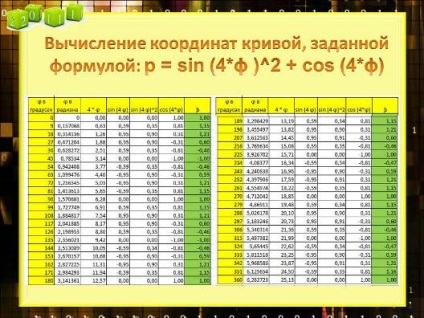
Побудова малюнка "Восьмілістнік":

Повернутися на сторінку Проект Системи координат: погляд у минуле і в даний
Спасибі, що відвідали нашу сторінку! Сподіваємося вам було цікаво.