Векторне поле називається соленоїдом. якщо існує таке векторне поле. для якого поле є полем роторів:.
Поле називається векторним потенціалом векторного поля.
Ознака соленоідальной векторного поля: векторне поле є соленоїдом тоді і тільки тоді, коли його дивергенція дорівнює нулю:. (14)
Рішення зразкового варіанта РГЗ
Завдання 1. Обчислити роботу сили при переміщенні точки прикладання сили вздовж заданої кривої L. від точки B до точки C. якщо значення параметра t в точках B і C задані:.
Для обчислення роботи використовуємо криволінійний інтеграл II роду (формула (3)):.
Складений криволінійний інтеграл зводимо до певного інтеграла, використовуючи параметричні рівняння кривої ВС:
Для заданої кривої отримуємо:
Таким чином, для знаходження роботи потрібно обчислити визначений інтеграл:
Зробимо заміну змінної в певному інтегралі:
Використовуємо прийом «підведення під знак диференціала частини підінтегральної функції»:
Відповідь: од. роботи.
Завдання 2. Заданий радіус-вектор рухається точки:
. Знайти вектори швидкості і прискорення руху цієї точки через 2 хвилини після початку руху.
Вектор-функція задана в координатної формі:.
Знайдемо перші і другі похідні її проекцій x (t), y (t) z (t) по аргументу t:
Знайдемо вектори швидкості і прискорення руху точки за формулами (4) і (5):
Через 2 хвилини після початку руху вектори швидкості і прискорення будуть:
Завдання 3. Дано векторне поле і рівняння площини d. 3x + y + 2z - 3 = 0. Потрібно:
1) знайти потік поля через площину трикутника АВС де А. В. і С - точки перетину площини d з координатними осями, в напрямку нормалі площини, орієнтованої «від початку координат»; побудувати креслення піраміди ОАВС. де О - початок координат;
2) використовуючи формулу Остроградського-Гаусса, обчислити потік поля через повну поверхню піраміди ОАВС в напрямку зовнішньої нормалі.
1) Щоб обчислити потік поля через площину трикутника АВС використовуємо формулу (6): ПАВС =. де D - проекція трикутника АВС на площину xOy. F - функція, що задає площину d. якої належить трикутник АВС.
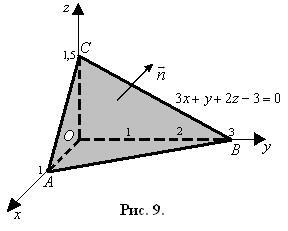
Побудуємо креслення піраміди, відклавши на координатних осях точки А. В. С і з'єднавши їх з початком координат O (рис. 9).
З рівняння площини d. 3x + y + 2z - 3 = 0, яке має вигляд F (x, y, z) = 0, знаходимо.
Оскільки всі три проекції градієнта позитивні, то цей вектор утворює з координатними осями гострі кути, тобто направлений «від початку координат» по відношенню до площини d. Це означає, що вектор і орт «зовнішньої» нормалі. вказаний в завданні, збігаються за напрямком, тому обчислення потоку через площину трикутника АВС зводиться до обчислення подвійного інтеграла: ПАВС = + (перед інтегралом ставимо знак «+»), де AOВ - проекція трикутника ABC на площину xOy.
Для розстановки меж інтегрування по трикутнику AOВ (рис. 10) знайдемо рівняння прямої АВ на площині xOy:
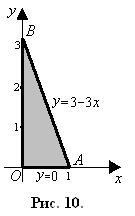
Таким чином, потік поля через площину трикутника АВС:
Обчислимо внутрішній інтеграл за змінною y:
Обчислимо зовнішній інтеграл за змінною х:
2) Щоб обчислити потік поля через повну поверхню піраміди ОАВС. скористаємося формулою Остроградського-Гаусса:
Знайдемо дивергенцію цього поля за формулою (8):. Для поля отримуємо:
Обчислимо потік поля через повну поверхню піраміди ОАВС:
. де - обсяг піраміди ОАВС. Цей обсяг можна обчислити, в такий спосіб:
В результаті отримуємо:.
Завдання 4. Перевірити, чи є векторне поле сили потенційним або соленоїдом. У разі потенційності поля знайти його потенціал і обчислити за допомогою потенціалу роботу сили при переміщенні одиничної маси з точки M (0,1,0) в точку N (-1,2,3).
Для перевірки потенційності векторного поля знайдемо його ротор за формулою (10):
Отже, поле потенційно.
Для перевірки соленоідальной поля знайдемо його дивергенцію за формулою (8):
Отже, полі не соленоідальной.
Для знаходження потенціалу U (x, y, z) векторного поля візьмемо фіксовану точку В (0,0,0), поточну точку С (x, y, z) і обчислимо криволінійний інтеграл по ламаній ВEKC. ланки якої паралельні осям координат і E (x, 0,0), K (x, y, 0) (див. рис. 7). За формулою (12) отримаємо:
Отримали потенціал поля. де С - довільна стала. Для перевірки рішення знайдемо градієнт потенціалу. . Отже, потенціал поля сили знайдено вірно.
Знайдемо роботу векторного поля при переміщенні одиничного маси з точки M (0,1,0) в точку N (-1,2,3) за формулою (11):
Відповіді: поле потенційно, що не соленоідальной; . де С - довільна постійна; робота А = -10.