3. Вільні радикали в хімічних реакціях
4. Дослідження радикалів, що утворюються при опроміненні органічних речовин. Загальні зауваження про можливості методу ЕПР в цій області
У 1944 р в Казанському університеті Є. К. Завойський проводив дослі-нання парамагнитной релаксації на високих частотах (10 7 -10 8 гц) при паралельній та перпендикулярної орієнтаціях змінного і постійного магнітних полів. Вперше здійснивши систематичне вивчення релаксації в перпендикулярних полях, він виявив в разі пара-магнітних солей (MnCl2. CuSO4 5H2 O і т.д.) інтенсивне резонансне поглинання високочастотної енергії при строго певних відносинах напруженості постійного магнітного поля до частоті. Так було відкрито нове фізичне явище, широко відоме тепер під назвою електронного парамагнітного резонансу (ЕПР).
У перші роки після цього відкриття метод ЕПР застосовувався в основному фізиками для вирішення приватних фізичних задач. В кінці сорокових років цей метод почав з успіхом застосовуватися для дослідження тонких деталей електронної структури парамагнітних іонів в кристалічних решітках різної симетрії. З початку п'ятдесятих років почався бурхливий застосування методу ЕПР до вирішення хімічних завдань. Це пов'язано з тим, що для сучасної хімії має надзвичайно велике значення з'ясування структури і хімічних властивостей парамагнітних частинок, які беруть участь в складних хімічних процесах. Це, з одного боку, парамагнітні іони металів перехідних груп періодичної системи, які є активними центрами величезного числа різних гетерогенних каталізаторів і входять до складу різних металоорганічних комплексів, що визначають активність складних органічних каталізаторів, в тому числі більшості біологічних ферментів. З іншого боку, детальне дослідження величезного числа складних хімічних реакцій в газовій і рідкій фазах, в тому числі фотохімічних, радіаційно-хімічних і біохімічних процесів, призвело до уявлення про надзвичайно велику поширеність в хімії вільно-радикальних і ланцюгових механізмів. У більшості випадків, і особливо в разі швидких процесів, висновок про радикальне характер того чи іншого процесу в зв'язку з труднощами безпосереднього виявлення, вимірювання концентрацій і встановлення будови вільних радикалів грунтувалося на непрямих кінетичних даних. Як буде показано нижче, метод ЕПР дозволив підійти до вирішення обох проблем, які можна об'єднати під загальною назвою - роль частинок з неспареним електроном в хімічних процесах, на абсолютно новому, значно вищому експериментальному і теоретичному рівні.
Метод ЕПР заснований на відомому ефекті Зеемана, що полягає в тому, що при введенні парамагнітної частки, яка характеризується квантовим числом S, в постійне магнітне поле її основний енергетичний рівень розщепиться на 2S + 1 підрівнів, відокремлених один від одного інтервалами енергії, рівними
де Н - напруженість магнітного поля;
- одиниця атомного магнетизму - магнетон Бора;
g - фактор спектроскопічного розщеплення, що визначає, по суті, величину ефективного магнітного моменту частки.
1. Умова ЕПР
Електрон, володіючи власним моментом кількості руху (спіном) і будучи електрично зарядженою часткою, має магнітний момент:
де S- вектор спінового кутового моменту (в одиницях h = h / 2π); μв- магнетон Бора (мкВ = ℮h / (2mc) = 9,27 * 10 -24 А * мІ; ℮- заряд електрона; m- маса спокою електрона; c-швидкість світла); g-безрозмірна величина (g- фактор Ланде), рівна для вільного електрона 2,00232.
У відсутності зовнішнього поля спінові вектори орієнтовані безладно, тобто спінові стану виродилися. При накладенні зовнішнього магнітного поля В гамельтоніан взаємодії з ним
запишеться у вигляді
Ось z збігається з напрямком поля. У загальному випадку паромагнітной часткою (при одному або декількох неспарених електронах) сумарний вектор S пов'язаний зі квантовим числом S відомим співвідношенням:
а його проекція, яка входить у вираз (3),
де ms-квантове число, яке може приймати значення від -S до + S (як і проекція Sz в одиницях ħ), тобто всього (2S + 1) значень.
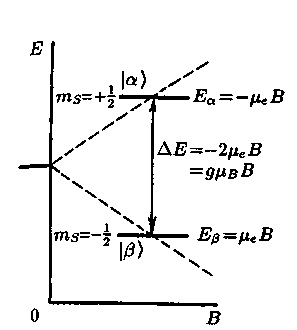
Мал. 1. Розщеплення спінових енергетичних рівнів електрона в залежності від індукції зовнішнього магнітного поля і індукований радіочастотним полем перехід
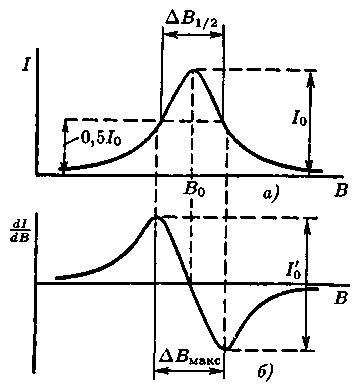
Мал. 2. Лінія спектра поглинаючи-ня ЕПР (а) і крива першої вироб-водної спектра ЕПР (б) для лоренцевих форми лінії
Оскільки при негативному заряді е негативний, е вибирається в рівнянні (1) позитивним. Для одного електрона S = 1/2 і можливі тільки дві орієнтації спинового вектора - по полю і проти поля, т. Е. Його проекції на напрям поля характеризуються двома значеннями квантового числа ms = ± 1/2.
Відповідні енергетичні стану, або зєємановських рівні, записуються у вигляді
Через різних знаків е і n стан з нижчою енергією взаємодії з полем у електрона на відміну від протона відповідає ms = 1/2 і позначається хвильової функцією стану | β>. Станом з більш високим значенням енергії відповідає ms = +1/2 і воно описується хвильової функцією | α>. Ці рівні показані на рис. 1. Переходи між ними можуть індукувати, як і в ЯМР, змінним радіочастотним полем, спрямованим перпендикулярно постійному зовнішньому магнітному полю, але в частотному діапазоні на три порядки вище, ніж в ЯМР, тобто в сантиметровому (міліметровому) діапазоні довжин хвиль.
Умовою магнітного резонансу є збіг різниці енергій рівнів, між якими відбувається перехід, залежить від зовнішнього поля B, з енергією кванта електромагнітного випромінювання, тобто
Для досягнення цієї умови використовують зазвичай розгортку по полю, тобто варіювання B при постійній частоті випромінювання (v = const). Резонансний сигнал в спектрі ЕПР зазвичай реєструється у вигляді залежності від напруженості поля першої похідної інтенсивності спектра поглинання, як це показано на малюнку 2, а, б, що дозволяє краще виявити особливості і дозволити структуру спектра.
2. Положення резонансного сигналу і g- фактор
Як параметр, що визначає положення лінії резонансного поглинання в спектрі ЕПР, можна розглядати так званий спектроскопічний фактор розщеплення Ланде або g-фактор, рівний відношенню електронного магнітного моменту до повного кутового моменту.
У теоретичній спектроскопії для вільних атомів (в газовій фазі) отримано такий вираз цього фактора:
де S-сумарний спин (спіновий число); L-сумарний орбітальний момент; J-повний кутовий момент. При рассел-саундерской спін-орбітальної (LS) зв'язку він приймає значення від | L + S | до | L-S |.
Чисто спіновий значення g-фактора для вільного електрона (S = 1/2, L = 0, J = 1/2) за формулою (8) виходить рівним g0 = 2, а наведене вище більш точне значення 2,00232 містить релятивістську поправку. Для неспареного електрона в багатьох вільних радикалів g-фактор також близький до цього значення і може відрізнятися від нього тільки в другому або навіть третьому знаку після коми, але взагалі, наприклад, у сполук перехідних металів та інших парамагнітних систем, значення g-фактора змінюються досить в широких межах (до декількох одиниць).
Відхилення g-фактора Δg від чисто спінового значення, обумовлене спін-орбітальної зв'язком, може бути як негативним, так і позитивним. Воно тим більше по абсолютній величині, чим сильніше спін-орбітальна взаємодія: зростає, наприклад, зі збільшенням порядкового номера елемента і зменшенням ΔE рівнів, між якими відбувається перехід. Прикладена зовнішнє магнітне поле Ввнеш індукує додатковий орбітальний момент кількості руху, а орбітальний рух електрона створює в свою чергу магнітне поле ВЛОК. рівному сумі прикладеного і наведеного полів ВЛОК = В зовн-Внавед; в цьому і полягає спін-орбітальна зв'язок. Чим більше наведене поле, тим менше локальне поле на спину системі і менше g-фактор, а напруженість зовнішнього поля Ввнеш для досягнення умови резонансу має бути вище - це відповідає негативному відхиленню (-Δg) від чисто спінового значення g-фактора, як показано на рис. 20.3 для g1.
Можлива інша ситуація, наприклад, такого розподілу неспарених електронів з різних орбиталям, що локальне поле виявляється збільшеним, тобто gi вище чисто спінового значення g0 і резонанс відбувається при більш низькому значенні Ввнеш, це відповідає позитивному відхиленню (+ Δg), як для g2 на рис.3.
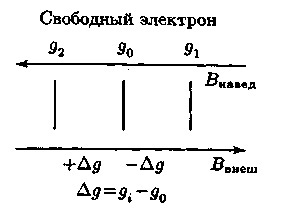
Рис.3. Схема зміни g-фактора в результаті спін-орбітальної зв'язку
Таким чином, поява резонансних піків при різних значеннях індукції зовнішнього магнітного поля, коли розгортка спектру проводиться по полю при частоті, залежить, перш за все, від g-фактора. Оскільки це так і оскільки g-фактор відображає характер спін-орбітальної взаємодії в системі, чисто формально і умовно цей параметр можна порівнювати з хімічним зсувом в спектрах ЯМР, хоча інформативність g-фактора нижче.
До сих пір g-фатор розглядався як скалярна величина, але це справедливо тільки при розгляді спектрів ЕПР ізотропних зразків, наприклад розчинів. У загальному випадку g-фактор - величина тензорна, і умови резонансу залежать від орієнтації паромагнітного об'єкта щодо поля. При вільному русі парамагнітних частинок в газі або розчині все орієнтації різновірогідні і відбувається в усередненні, так що тензор стає сферично симетричним, тобто характеризується єдиним параметром g. Те ж ставиться до інших ізотропним системам. На практиці, однак, часто досліджують спектри ЕПР анізотропних систем, таких як заморожені розчини, парамагнітні центри в монокристалах, об'єкти в матрицях, різні тверді зразки та інші. У всіх цих випадках g-фактор повинен розглядатися як симетричний (має осьову симетрію) або асиметричний (неаксеальний) тензор. Його при відповідному виборі системи координат завжди можна діагоналізіровать і отримати три головних значення g-фактора: gхх. gyy. gzz.