Список з пропусками (англ. Skip list) - пошукова структура даних, що реалізує інтерфейс впорядкованої множини, дозволяє проводити операції пошуку, додавання і видалення елемента в списку за досить короткий час.
Пошук елемента в списку проводиться за; додавання і видалення елеметов відбувається за той же час, що і пошук, однак ці операції можуть уповільнити пошук в структурі.
[Ред] Побудова
Список з пропусками будується на основі існуючого однозв'язного відсортованого списку.
Додавши додаткові рівні, кожен з яких представляє попередній рівень без непарних елементів, ми отримаємо можливість здійснювати пошук, вставку і видалення елементів подібно операціями з двійковим деревом пошуку. Відповідно, асимптотика цих операцій становитиме.
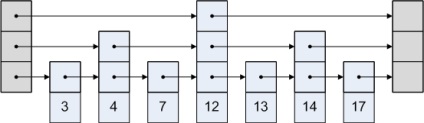
[Ред] Операції над структурою
[Ред] Пошук елемента
Припустимо, що в нашому списку з пропусками існують рівнів, при цьому першим рівнем () буде вихідний список.
В такому випадку алгоритм пошуку в цій структурі буде представляти із себе наступні операції:
- Починаємо пошук елемента у верхньому списку (), розглянемо перший елемент
- Переходити до іншого збігу, поки значення в наступної комірки менше або дорівнює ключу
- Переміститися на один рівень вниз і перейти до пункту 2. Якщо розглянутий елемент знаходиться на нижньому рівні - вийти з пошуку
Приклад пошуку числа в списку з опису:
Розглянемо час роботи для списку з двома рівнями. Тоді час роботи алгоритму пошуку буде залежати від кількості елементів на рівні. Уявімо, що на цей рівень у нас випадковим чином потрапило кілька елементів. Отже в гіршому випадку пошуку ми отримаємо наступну оцінку на час роботи:
Мінімізуючи, ми отримуємо, що
В результаті час за яке ми знайдемо елемент в списку з пропусками з двома рівнями буде дорівнювати:
Також можна переконатися, що список з пропусками, що має рівнів, буде найкраще працювати з елементами на рівні; час роботи такого списку дорівнюватиме. Для рівнів же час роботи складе
[Ред] Вставка елементу
Для вставки елемента в список з пропусками, нам необхідно виконати наступні кроки:
- Знайти за допомогою алгоритму пошуку позицію, куди нам треба вставити цей елемент
- Вставити наш елемент в нижній рівень списку з пропусками
- «Підкинути монетку» і в залежності від результату проштовхнути елемент на рівень вище
- Повторювати попередній крок до тих пір, поки у нас «подброс монетки» дає позитивний результат
Таким чином, якщо використовувати чесну монету, то математичне сподівання кількості елементів на другому рівні дорівнює, на третьому рівні та т.д. На рівні у нас виявиться один елемент. Ну і відповідно ймовірності потрапити елементу на другий рівень - це, на третій і т.д. Імовірність потрапити на рівень дорівнює.
Використовуючи монетку з розподілом відмінним від,, можна впливати на кількість елементів на верхніх рівнях. Так, наприклад, при використанні монети з розподілом>, математичне сподівання кількості елементів на рівні одно, кожен рівень буде складати від попереднього; час пошуку дорівнюватиме. Відповідно при чесній монетку і рівнів отримуємо оцінку, отриману раніше. Для крайніх розподілів:
- -
- - (якщо дозволити додавання нових рівнів при проштовхуванні елемента після кидка монетки; інакше)
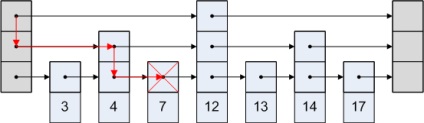
[Ред] Видалення елемента
Алгоритм видалення досить тривіальний.
- Знайти видаляється елемент
- Видалити його з усіх рівнів
[Ред] Псевдокод
Наочний, але не дуже ефективний по пам'яті варіант списку з пропусками.
У вузлах списку зберігаються:
- - наступний вузол
- - той же вузол на наступному рівні
- - дані типу T
- - ключ типу K
Пошук елемента по ключу:
[Ред] Застосування
- Бази даних
- Розподілені обчислення і p2p
- Масштабуються паралельні пріоритетні черги і словники
У обчислювальної геометрії широко застосовуються структури на основі списку з пропусками.
[Ред.] Також
Структури на основі списку з пропусками: