
Сучасні двигуни для 3D-візуалізації, що використовуються в іграх і мультимедіа, вражають своєю складністю в плані математики та програмування. Відповідно, результат їх роботи чудовий.
Багато розробники помилково вважають, що створення навіть найпростішого 3D-додатки з нуля вимагає нелюдських знань і зусиль. На щастя, це не зовсім так. Більш того, при наявності комп'ютера і вільного часу, можна створити щось подібне самостійно. Давайте поглянемо на процес розробки нашого власного движка для 3D-візуалізації.
Само собою, якщо ви хочете створити яке-небудь велике 3D-додаток з плавною анімацією, вам краще використовувати OpenGL / WebGL. Однак, маючи базове уявлення про те, як влаштовані подібні двигуни, робота з більш складними двигунами буде здаватися в рази простіше.
У цій статті я постараюся пояснити базовий 3D-рендеринг з ортографической проекцією, просту трикутну растеризування (процес, зворотний векторизації), Z-буферизацію і плоске затінення. Я не буду загострювати свою увагу на таких речах, як оптимізація, текстури і різні налаштування освітлення - якщо вам це потрібно, спробуйте використовувати більш підходящі для цього інструменти, на зразок OpenGL (існує безліч бібліотек, що дозволяють вам працювати з OpenGL, навіть використовуючи Java).
Приклади коду будуть на Java, але самі ідеї можуть, зрозуміло, бути застосовані для будь-якого іншого мови за вашим вибором.
Досить базікати - давайте приступимо до справи!
Для початку, давайте помістимо хоч що-небудь на екран. Для цього, я буду використовувати просте додаток, в якому буде відображатися наше відрендерене зображення і два скроллера для обертання.
Результат повинен виглядати ось так:

Тепер давайте додамо деякі моделі - вершини і трикутники. Вершина - це просто структура для зберігання наших трьох координат (X, Y і Z), а трикутник з'єднує разом три вершини і містить їх колір.
Тут я буду вважати, що X означає переміщення вліво-вправо, Y - вгору-вниз, а Z буде глибиною (так, що вісь Z перпендикулярна вашому екрану). Позитивна Z буде означати «ближче до користувача».
Як приклад я вибрав тетраедр як найпростішу фігуру, про яку згадав - потрібно всього 4 трикутника, щоб описати її.
Код також буде досить простим - ми просто створюємо 4 трикутника і додаємо їх в ArrayList:
В результаті ми отримаємо фігуру, центр якої знаходиться в початку координат (0, 0, 0), що досить зручно, так як ми будемо обертати фігуру щодо цієї точки.
Тепер давайте додамо все це на екран. Спершу ми не будемо додавати можливість обертання і просто отрісуем каркасне уявлення фігури. Так як ми використовуємо ортографической проекцію, це досить просто - досить прибрати координату Z і намалювати наші трикутники.
Зауважте, що зараз я зробив все перетворення до відтворення трикутників. Це зроблено, щоб для того, що б помістити наш центр (0, 0, 0) в центр екрану - за замовчуванням початок координат знаходиться в лівому верхньому кутку екрану. Після компіляції ви повинні отримати:

Ви можете не повірити, але це наш тетраедр в ортогональної проекції, чесно!
Тепер нам потрібно додати обертання. Для цього мені потрібно буде трохи відійти від теми і поговорити про використання матриць і про те, як з їх допомогою досягти тривимірної трансформації 3D-точок.
Існує багато шляхів маніпулювати 3D-точками, але самий гнучкий з них - це використання матричного множення. Ідея полягає в тому, щоб показати точки у вигляді вектора розміру 3 × 1, а перехід - це, власне, домноженіе на матрицю розміру 3 × 3.
Візьмемо наш вхідний вектор A:
І помножимо його на так звану матрицю трансформації T, щоб отримати в результаті вихідний вектор B:
Наприклад, ось як буде виглядати трансформація, якщо ми помножимо на 2:
Ви не можете описати будь-яку можливу трансформацію, використовуючи матриці розміру 3 × 3 - наприклад, якщо перехід відбувається за межі простору. Ви можете використовувати матриці розміру 4 × 4, роблячи перекіс в 4D-простір, але про це не в цій статті.
Трансформації, які нам знадобляться тут - масштабування і обертання.
Будь-яке обертання в 3D-просторі може бути виражено в 3 примітивних вирощених: обертання в площині XY, обертання в площині YZ і обертання в площині XZ. Ми можемо записати матриці трансформації для кожного з даних обертань наступним шляхом:
І ось тут починається магія: якщо вам потрібно спочатку зробити обертання точки в площині XY, використовуючи матрицю трансформації T1, і потім зробити обертання цієї точки в площині YZ, використовуючи матрицю трансформації T2, то ви можете просто помножити T1 на T2 і отримати одну матрицю, яка опише все обертання:
Це дуже корисна оптимізація - замість того, щоб постійно рахувати обертання на кожній точці, ми заздалегідь вважаємо одну матрицю і потім використовуємо її.
Що ж, досить страшною математики, давайте повернемося до коду. Створимо службовий клас Matrix3, який буде обробляти перемноження типу "матриця-матриця" та "вектор-матриця":
Тепер можна і оживити наші скролери обертання. Горизонтальний скроллер контролюватиме обертання вліво-вправо (XZ), а вертикальний скроллер контролюватиме обертання вгору-вниз (YZ).
Давайте створимо нашу матрицю обертання:
Вам також буде потрібно додати слухачів на скролери, щоб забезпечити оновлення зображення, коли ви будете тягти їх вгору-вниз або вправо-вліво.
Як ви, напевно, вже помітили, обертання вгору-вниз ще не працює. Додамо ці рядки в код:
До сих пір ми малювали тільки каркасне представлення нашої фігури. Тепер давайте заповнимо його чимось. Для цього нам потрібно спочатку растеризувати трикутник - представити його у вигляді пікселів на екрані.
Ідея полягає в тому, щоб порахувати барицентричні координати для кожного пікселя, який може лежати всередині нашого трикутника і виключити ті, що поза його межами. Наступний фрагмент містить алгоритм. Зверніть увагу на те, як ми стали безпосередньо звертатися до пікселів зображення.
Досить багато коду, але тепер у нас є кольоровий тетраедр на екрані.

Якщо ви пограли з Демко, то ви помітите, що не все зроблено ідеально - наприклад, синій трикутник завжди вище інших. Так відбувається тому, що ми отрісовиваємих наші трикутники один за іншим. Синій тут - останній, тому він малюється поверх інших.
Щоб виправити це, давайте розглянемо Z-буферизацію. Ідея полягає в тому, щоб в процесі растеризації створити проміжний масив, який буде зберігати в собі відстань до останнього видимого елемента на кожному з пікселів. Роблячи растеризування трикутників, ми будемо перевіряти, чи менше відстань до пікселя, ніж відстань до попереднього, і зафарбовувати його тільки в тому випадку, якщо він знаходиться поверх інших.
Тепер видно, що у нашого тетраедра є одна біла сторона:

Ось ми і отримали працюючий двигун для 3D-візуалізації!
Але і це ще не кінець. У реальному світі сприйняття будь-якого кольору змінюється в залежності від положення джерел світла - якщо на поверхню падає лише невелика кількість світла, то вона бачиться більш темною.
У комп'ютерній графіці ми можемо досягти подібного ефекту за допомогою так званого «затінення» - зміни кольору поверхні в залежності від кута нахилу і відстані щодо джерела світла.
Найпростіша форма затінення - це плоске затінення. Цей спосіб враховує лише кут між поверхнею, нормаль і напрям джерела світла. Вам всього лише потрібно знайти косинус кута між двома векторами і помножити колір на вийшло значення. Такий підхід дуже простий і ефективний, тому він часто використовується для високошвидкісного рендеринга, коли найбільш просунуті технології затінення занадто неефективні.
Для початку нам потрібно порахувати вектор нормалі для нашого трикутника. Якщо у нас є трикутник ABC, ми можемо порахувати його вектор нормалі, розрахувавши векторний добуток векторів AB і AC і поділивши отриманий вектор на його довжину.
Векторний добуток - це бінарна операція на двох векторах, які визначені в 3D просторі ось так:
Ось так виглядає візуальне уявлення того, що робить наше векторний добуток:
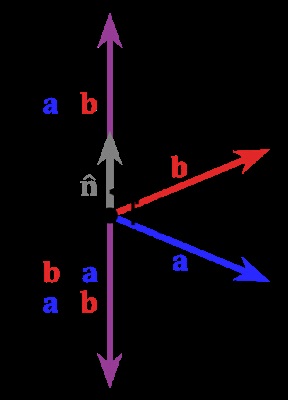
Тепер нам потрібно порахувати косинус між нормаллю трикутника і напрямком світла. Для спрощення будемо вважати, що наше джерело світла розташований прямо за камерою на будь-якому відстані (така конфігурація називається «направлене світло») - таким чином, наше джерело світла буде знаходитися в точці (0, 0, 1).
Косинус кута між векторами можна порахувати за формулою:
Де || A || - довжина вектора, а чисельник - скалярний добуток векторів A і B:
Зверніть увагу на те, що довжина вектора напрямку світла дорівнює 1, так само, як і довжина нормалі трикутника (ми вже нормалізували це). Таким чином, формула просто перетворюється в це:
Зауважте, що тільки Z компонент напрямки світла не дорівнює нулю, так що ми можемо просто все спростити:
У коді це все виглядає тривіально:
Ми опускаємо знак результату, тому що для наших цілей нам не важливо, яка сторона трикутника дивиться на камеру. У реальному додатку вам потрібно буде відслідковувати це і застосовувати затінення відповідно.
Тепер, отримавши наш коефіцієнт затінення, ми можемо застосувати його до кольору нашого трикутника. Простий варіант буде виглядати якось так:
Код буде давати нам деякі ефекти затінення, але спадати вони будуть куди швидше, ніж нам потрібно. Так відбувається, тому що в Java використовується спектр кольорів sRGB.
Так що нам потрібно конвертувати кожен колір в лінійний формат, застосувати затінення і потім конвертувати назад. Реальний перехід з sRGB до лінійного RGB - досить трудомісткий процес, так що я не буду виконувати повний перелік завдань тут. Замість цього, я зроблю щось наближене до цього.
І тепер ми бачимо, як наш тетраедр пожвавлюється. У нас є працюючий двигун для 3D візуалізації з квітами, освітленням, затінення, і зайняло це близько 200 рядків коду - непогано!
Ось невеликий бонус для вас - ви можете швидко створити фігуру, наближену до сфери зі свого тетраедра. Цього можна досягти шляхом розбивання кожного трикутника на 4 маленьких і «надуваючи».
Ось що повинно у вас вийти:

Я б закінчив цю статтю, порекомендувавши одну цікаву книгу: "Основи 3D-математики для графіки і розробки ігор". У ній ви можете знайти детальне пояснення процесу рендеринга і математики в цьому процесі. Її варто прочитати, якщо вам цікаві движки для рендеринга.