п.1.1 Поняття вектора
Багато фізичні величини, наприклад сила, переміщення матеріальної точки, швидкість, характеризуються не тільки своїм числовим значенням, а й напрямком на площині або в просторі. Такі фізичні величини називаються векторними величинами (або коротко векторами).
Розглянемо приклад. Нехай на тіло діє сила в 8Н. На малюнку таку силу зображують відрізком зі стрілкою (рис.1). Стрілка вказує напрямок прикладеної сили, а довжина відрізка відповідає в обраному масштабі числовим значенням сили.
Відволікаючись від конкретних властивостей фізичних векторних величин, ми приходимо до геометричного поняття вектора.
Розглянемо довільний відрізок. На ньому можна вказати два напрямки: від одного кінця до іншого і навпаки (рис.1).
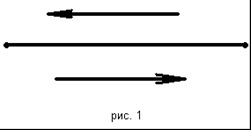
Щоб вибрати один із напрямів, один кінець відрізка назвемо початком. а інший - кінцем і будемо вважати, що відрізок спрямований від початку до кінця.
Определеніе.Отрезок, для якого вказано, який з його кінців вважається початком, а який - кінцем, називається спрямованим відрізком або вектором.
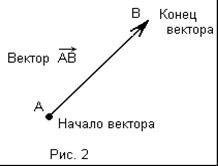
На малюнках вектор зображується відрізком зі стрілкою, яка показує напрямок вектора. Вектори позначають двома великими латинськими буквами зі стрілкою над ними, наприклад. Перша буква позначає початок вектора, друга - кінець (рис.2).
На малюнку 3, а зображені вектори
; точки - початку даних векторів, а - їх кінці. Вектори часто позначають і однієї малої латинською буквою зі стрілкою над нею: (рис.3, б).

Для подальшого доцільно домовитися, що будь-яка точка площині також є вектором. У цьому випадку вектор називається нульовим. Початок нульового вектора збігається з його кінцем, на малюнку такий вектор зображується однією точкою. Якщо, наприклад, точка, яка зображує нульовий вектор, позначена буквою М, то даний вектор можна позначити (рис.3, а). Нульовий вектор позначається також символом. На малюнку 3, а ненульові, а вектор нульової.
Довгою або модулем ненульового вектора називається довжина відрізка АВ. Довжина вектора (вектора) позначається так. Довжина нульового вектора вважається рівною нулю.
п.1.2 Рівність векторів
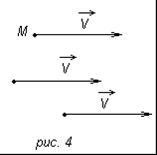
Перш ніж дати визначення рівних векторів, звернемося до прикладу. Розглянемо рух тіла, при якому всі його точки рухаються з однієї і тієї ж швидкістю і в одному і тому ж напрямку. Швидкість кожної точки М тіла є векторною величиною, тому її можна зобразити спрямованим відрізком, початок якого збігається з точкою М (рис.4). Так як всі точки тіла рухаються з однієї і тієї ж швидкістю, то все спрямовані відрізки, що зображують швидкості цих точок, мають один і той же напрямок і довжини їх рівні.
Цей приклад підказує нам, як визначити рівність векторів. Попередньо вводиться поняття колінеарних векторів.
Определеніе.Ненулевие вектори називаються колінеарними, якщо вони лежать на одній прямій, або на паралельних прямих; нульовий вектор вважається колінеарну будь-якому вектору.
Якщо два ненульових вектора колінеарні, то вони можуть бути спрямовані або однаково, або протилежно. Ці вектора називають відповідно сонаправленнимі і протилежно спрямованими, при цьому використовується наступне позначення:
Початок нульового вектора збігається з його кінцем, тому нульовий вектор не має якого-небудь певного напрямку. Інакше кажучи, будь-який напрямок можна вважати напрямком нульового вектора. Домовилися вважати, що нульовий вектор сонаправлени з будь-яким вектором.
Тепер, спираючись на вищесказане, легко дати визначення рівних векторів.
Визначення. Вектори називаються рівними, якщо вони сонаправлени і їх довжини рівні.
п.1.3 Відкладання вектора від даної точки
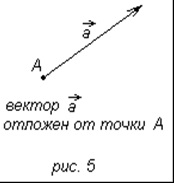
Якщо точка А - початок вектора. то кажуть, що вектор відкладений від точки А (рис.5). Доводиться наступне твердження:
Від будь-якої точки М можна відкласти вектор, рівний даному вектору. і при тому тільки один.
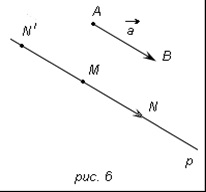
Справді, якщо - нульовий вектор, то шуканим вектором є вектор. Припустимо, що вектор ненульовий, а точки А і В - його початок і кінець. Проведемо через точку М пряму р. паралельну АВ (рис.6) (якщо М - точка прямої АВ. то в якості прямої р візьмемо саму пряму АВ). На пряме р відкладемо відрізки MN і. рівні відрізку АВ. і виберемо з векторів той, який сонаправлени з вектором (на рис.6 вектор). Цей вектор і є шуканим вектором, рівним вектору. Варто звернути увагу на висновок про єдиності такого вектора: такий висновок робиться на основі малюнка.
Зауваження. Рівні вектори, відкладені від різних точок, часто позначають однією і тією ж буквою. Так позначені, наприклад, рівні вектори швидкості різних точок на малюнку 4. Іноді про такі вектори кажуть, що це один і той же вектор, але відкладений від різних точок.
Перейти до завантаження файлу