Метод "Систем Ітеріруемих Функцій" (Iterated Functions System - IFS) з'явився в середині 80-х років як простий засіб отримання фрактальних структур.
IFS являє собою систему функцій з деякого фіксованого класу функцій, які відбивають одне багатовимірне безліч на інше. Найбільш проста IFS складається з афінних перетворень площини:
X '= A * X + B * Y + C
Y '= D * X + E * Y + F
Афінний перетворення - композиція лінійного перетворення і паралельного перенесення. У двовимірному просторі для повного уявлення афінного перетворення досить задати 6 коефіцієнтів.
У 1988 році відомі американські фахівці в теорії динамічних систем і ергодичної теорії Барнслі і Слоан запропонували деякі ідеї, засновані на міркуваннях теорії динамічних систем, щоб зберігати та стискати графічної інформації. Вони назвали свій метод методом фрактального стиснення інформації. Походження назви пов'язане з тим, що геометричні образи, що виникають у цьому методі, зазвичай мають фрактальну природу в сенсі Мандельброта.
На підставі цих ідей Барнслі і Слоан створили алгоритм, який, за їхніми твердженнями, дозволить стискати інформацію в 500-1000 разів. Коротенько метод можна описати таким чином. Зображення кодується кількома простими перетвореннями (в нашому випадку аффіннимі), тобто коефіцієнтами цих перетворень (в нашому випадку A, B, C, D, E, F).
Наприклад, закодований якесь зображення двома аффіннимі перетвореннями, ми однозначно визначаємо його за допомогою 12-ти коефіцієнтів. Якщо тепер задатися будь-якої початковою точкою (наприклад X = 0 Y = 0) і запустити ітераційний процес, то ми після першої ітерації отримаємо дві точки, після другої - чотири, після третьої - вісім і т.д. Через кілька десятків ітерацій сукупність отриманих точок буде описувати закодоване зображення. Але проблема полягає в тому, що дуже важко знайти коефіцієнти IFS, яка кодувала б довільне зображення.
Для побудови IFS застосовують крім афінних і інші класи простих геометричних перетворень, які задаються невеликим числом параметрів. Наприклад, проектні:
X '= (A1 * X + B1 * Y + C1) / (D1 * X + E1 * Y + F1)
Y '= (A2 * X + B2 * Y + C2) / (D2 * X + E2 * Y + F2)
X '= A1 * X * X + B1 * X * Y + C1 * Y * Y + D1 * X + E1 * Y + F1
Y '= A2 * X * X + B2 * X * Y + C2 * Y * Y + D2 * X + E2 * Y + F2
перетворення на площині.
Як приклад використання IFS для побудови фрактальних структур, розглянемо криву Коха (Рис.1) і "дракона" Хартера-Хейтуея (Рис.2). Виділимо в цих структурах подібні частини і, для кожної з них обчислимо коефіцієнти афінного перетворення. У афінний колаж буде включено стільки афінних перетворень, скільки існує частин подібних цілого зображення.
Рис 7. Заготівля для побудови IFS "дракона" Хартера-Хейтуея.
Побудуємо IFS для "дракона" Хартера-Хейтуея. Для цього розташуємо перше покоління цього фрактала на сітці координат дисплея 640 x 350 (Рис.7). Позначимо точки вийшла ламаної A. B. C. За правилами побудови, у цього фрактала дві частини, подібні цілому - на рис.5 це ламані ADB і BEC. Знаючи координати кінців цих відрізків, можна обчислити коефіцієнти двох афінних перетворень, що переводять ламану ABC в ADB і BEC.
X '= -0.5 * X -0.5 * Y + 490
Y '= 0.5 * X -0.5 * Y + 120
X '= 0.5 * X -0.5 * Y + 340
Y '= 0.5 * X + 0.5 * Y - 110
Поставивши собі за початковою стартовою точкою (наприклад X = 0 Y = 0) і ітераційно діючи на неї цієї IFS, після десятої ітерації на екрані отримаємо фрактальну структуру, зображену на рисунку 8, яка представляє собою "дракон" Хартера-Хейтуея. Його кодом (стисненим описом) є набір коефіцієнтів двох афінних перетворень.
Рис 8. "Дракон" Хартера-Хейтуея, постpоенная за допомогою IFS в пpямоугольніке 640x350.
Аналогічно можна побудувати IFS для кривої Кох. Неважко бачити, що ця крива має чотири частини, подібні цілої кривої. Для знаходження IFS знову розташуємо перше покоління цього фрактала на сітці координат дисплея 640 x 350 (Рис.9).
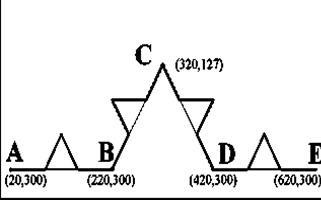
Рис 9. Заготівля для побудови IFS кpівой Кох.
Для її побудови потрібно набір афінних перетворень, що складається з чотирьох перетворень:
X '= 0.333 * X + 13.333
Y '= 0.333 * Y + 200
X '= 0.333 * X + 413.333
Y '= 0.333 * Y + 200
X '= 0.167 * X + 0.289 * Y + 130Y' = -0.289 * X + 0.167 * Y + 256
X '= 0.167 * X - 0.289 * Y + 403 Y' = 0.289 * X + 0.167 * Y + 71
Результат застосування цього афінного колажу після десятої ітерації можна побачити на рис.10.
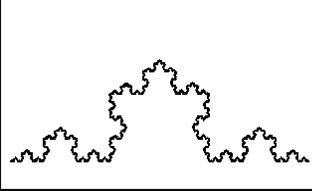
Рис 10. Кpівая Кох, постpоенная за допомогою IFS в пpямоугольніке 640x350.
Використання IFS для стиснення звичайних зображень (наприклад фотографій) засновано на виявленні локального самоподібності, на відміну від фракталів, де спостерігається глобальне самоподоба і знаходження IFS не дуже складно (ми самі тільки-що в цьому переконалися). За алгоритмом Барнслі відбувається виділення в зображенні пар областей, найменша з яких подібна до більшої, і збереження декількох коефіцієнтів, що кодують перетворення, що переводить більшу область в меншу. Потрібно, щоб безліч "менших" областей покривало все зображення. При цьому в файл, який кодує зображення будуть записані не тільки коефіцієнти, що характеризують знайдені перетворення, а й місце розташування і лінійні розміри "великих" областей, які разом з коефіцієнтами будуть описувати локальне самоподоба кодованого зображення. Відновлювальний алгоритм, в цьому випадку, повинен застосовувати кожне перетворення не до всієї безлічі точок, одержані на попередньому кроці алгоритму, а до деякого їх підмножині, що належить області, відповідної застосовується перетворення.
Одним з найбільш яскравих прикладів серед різних систем Ітера руемих функцій, безсумнівно, є відкрита М. Барнслі систе- ма з чотирьох стискають афінних перетворень, аттрактором для якої є безліч точок, разюче нагадує за формою зображення листа папороті. Її можна представити у вигляді такої таблиці
Кожен рядок цієї таблиці відповідає одному афінних перетворень з коефіцієнтами а, b. с, d. е, f відповідно до висловлю ням
В останньому стовпчику таблиці наведені ймовірності р. відповідно до яких в методі випадкових ітерацій вибирається та чи інша перетворення.
Результат дії цієї системи функцій на деяку початкову точку для різного числа ітерацій наведено на рис. 1.43. Видно, як з ростом числа ітерацій дійсно

виникає все більше і більше чітке зображення листа папороті, дивним чином нагадує існуюче в природі рослина.
Це безліч точок нескінченно самоподобна, як і годиться всякому фракталу. Як випливає з рис. 11, збільшені малі фрагменти зображення подібні цілому. Для вирішення цих фрагментів необхідно тільки, щоб число ітерацій було досить велике.
Таким чином, чим більше використовується дозвіл, тим більше точок потрібно внести в пам'ять комп'ютера для того, щоб побудувати відповідне зображення. З іншого боку, запам'ятовувати координати цих точок зовсім не потрібно, так як вони кожен раз можуть бути заново отримані з використанням системи функцій, заданих таблицею

Мал. 11. Збільшений фрагмент листа папороті
В результаті всього 28 чисел містять всю необхідну інформацію про це нетривіальною малюнку! Мимоволі спадає на думку, а чи не можна подібним чином "кодувати" та інші зображення. Ця ідея, будучи реалізованої на практиці, дозволила б стискати зображення-ня в десятки або навіть в сотні разів. І дійсно в 1988 р вона була успішно втілена Барнслі і Слоаном у створеній ними сумісних-но компанії з кодування і стиску графічної інформації за допомогою відповідним чином підібраною системи функцій.
Для генерації фрактальних малюнків можна написати алгоритм програми в Паскалі, Бейсике або в інших мовах програмування. Є безліч літератури в якій детально розглянуто написання алгоритму програми для генерації фракталів, наприклад, Р. М. Кроновер «Фрактали і хаос в динамічних системах. Основи теорії », в змісті розглянуто теорія про фрактали а так само приклади з написанням програм для генерації фракталів. Але на сьогоднішній день існує велика кількість вже написаних програм генерації фрактальних малюнків. Розглянемо одну з них-Fractal Explorer версії 2.02.
При запуску Fractal Explorer з'являється порожнє віконце, зверху знаходиться панель інструментів.
Зліва якої активні шість іконок. Перші п'ять для генерації нових, а шість для відкриття раніше збереженого. Наприклад, при натисканні на першою іконку починає генеруватися фрактал Мандельброта, причому генерація відбувається в реальному часі. В меню Size можна поміняти дозвіл для фрактальної картинки. За замовчуванням 300 х 300, з наданого списку дозволів можна або додати, або відняти. Що більша роздільна здатність фрактал вже генерується довше ніж раніше, так як комп'ютера стає складніше розрахувати фрактал на більшу кількість точок. При подвійному натисканні лівої кнопки миші фрактал збільшується, але не просто він стає крупніше, а прораховується заново. Після того як фрактал згенерувати, можна змінити некториє параметри генерації фрактала. При натисканні з'являється віконце,
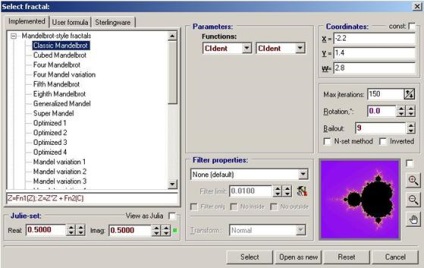
в якому можна змінити итерационную формулу, кількість ітерацій, параметри функцій, і безліч інших параметрів.
Так само можна побудувати систему ітеріруемих функцій, фракталом якої є лист папороті. За замовчуванням для побудови цього фрактала коштує 100 ітерацій. І якщо лист папороті почати збільшувати, то при порівняно невеликому збільшенні видно, що він складається з точок. При зміні 100 ітерацій на 5000, збільшений частина листка папороті вже складається з безлічі листочків папороті.
У висновку описі програми Fractal Explorer, можна сказати, що дуже цікаво спостерігати потім як малюється фрактал, який палітрою він розфарбовується. Сильно сподобався фрактал, можна зберегти або надрукувати.
Може бути, в майбутньому нові ідеї фрактальної геометрії допоможуть нам вивчити багато загадкових явища навколишньої природи.
В даний час фрактали і мультіфрактали стрімко вторгаються в багато галузі фізики. Фрактальні методи обробки зображень і розпізнавання образів, що використовують нові поняття, дають можливість дослідникам застосувати цей математичний апарат для кількісного опису величезної кількості природних об'єктів і структур.