ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Геометричний сенс рівності видно з рис. 11. Тут х - це половина дуги АВ, а sin х - половина відповідної хорди. Очевидно, що в міру зближення точок А і В довжина хорди все точніше наближається до довжини дуги. З того ж малюнка нескладно отримати нерівність
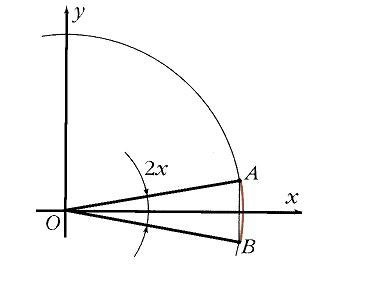
Формулу (*) математики називають чудовим межею. З неї, зокрема, випливає, що sin х »х при малих х.
Функції у = tg х, у = ctg х. Дві інші тригонометричні функції - тангенс і котангенс найпростіше визначити як відносини вже відомих нам синуса і косинуса:
Як синус і косинус, тангенс і котангенс - функції періодичні, але їх періоди рівні p. тобто вони вдвічі менше, ніж у синуса і косинуса. Причина цього зрозуміла: якщо синус і косинус обидва поміняють знаки, то їх ставлення не зміниться.
Оскільки в знаменнику тангенса знаходиться косинус, то тангенс не визначений в тих точках, де косинус дорівнює 0, - коли х = p / 2 + k p. У всіх інших точках він монотонно зростає. Прямі х = p / 2 + k p для тангенса є вертикальними асимптотами. У точках k p тангенс і кутовий коефіцієнт складають 0 і 1 відповідно (рис. 12).
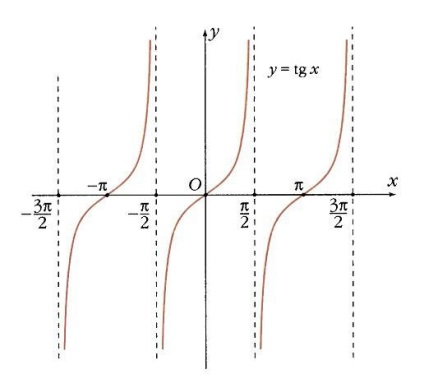
Котангенс не визначений там, де синус дорівнює 0 (коли х = k p). В інших точках він монотонно убуває, а прямі х = k p- його вертикальні асимптоти. У точках х = p / 2 + k p котангенс звертається в 0, а кутовий коефіцієнт в цих точках дорівнює -1 (рис. 13).
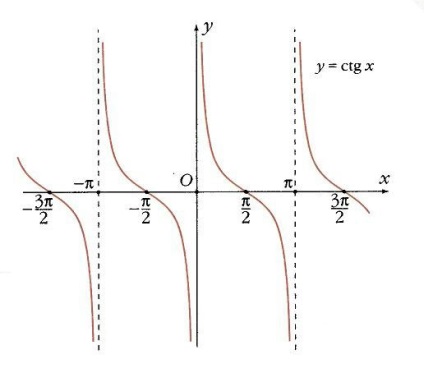
Парність і періодичність.
Функція називається парною, якщо f (-x) = f (x). Функції косинус і секанс - парні, а синус, тангенс, котангенс і косеканс - функції непарні:
sin (-α) = - sin α
tg (-α) = - tg α